2 简单国民收入决定原理

:material-circle-edit-outline: 约 523 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

2.1 国民经济循环模型

2.1.1 两部门经济模型

• 总供给：\(Y=C+S\)
• 总需求：\(Y=C+I\)

两部门经济均衡国民收入的决定条件为投资等于储蓄，即 \(I=S\)

含义：厂商生产出来的产品中，消费者没有购买的那部分产品，刚好等于厂商需要购买的投资品，那么产品市场的供求也相等

2.1.2 三部门经济模型

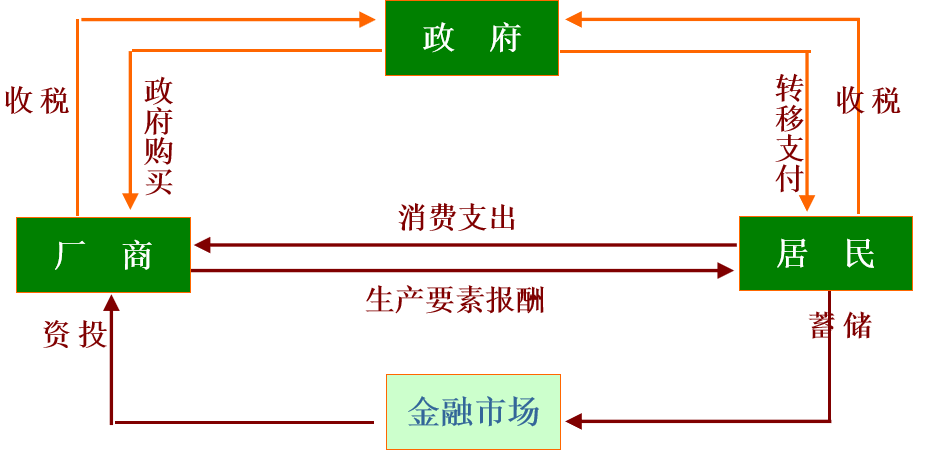
• 总供给：\(Y=C+S+T\)
  • 净税收 T﹦税收 - 转移支付
• 总需求：\(Y=C+I+G\)

2.1.3 四部门经济模型

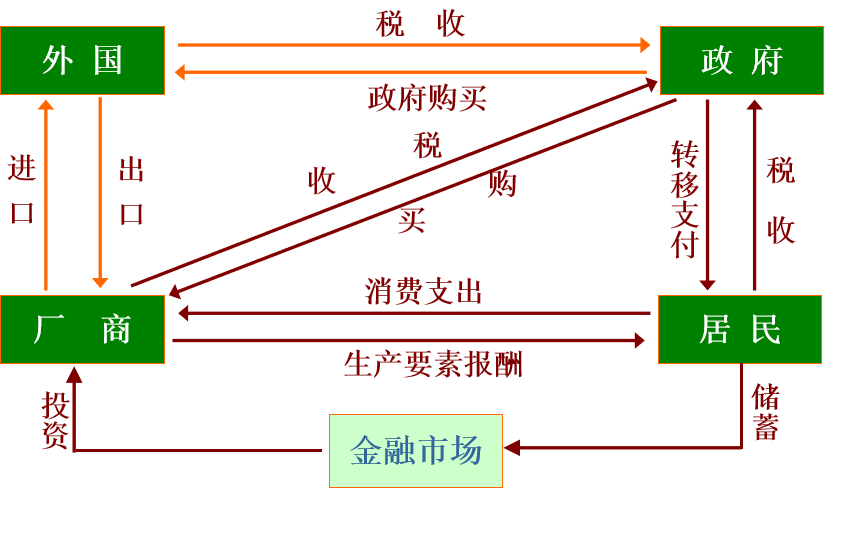
• 总供给：\(Y=C﹢S﹢T\)
• 总需求：\(Y=C+I+G+（X-M）\)

\(X\) 是出口，\(M\) 是进口，\(NX\) 是净出口

在四部门经济中，均衡总产出也可根据“投资=储蓄”的条件来确定，只不过四部门经济中的投资应是“国民总投资”，而储蓄应是“国民总储蓄”，即

\(I=S+（T-G）+（M-X）\)

2.2 均衡国民收入决定原理

2.2.2凯恩斯简单国民收入决定模型

• 模型假设
  1. 两部门模型
  2. 价格不受需求和供给影响
  3. 不考虑折旧和公司未分配利润

有效需求决定供给

均衡国民收入是总供给与总需求相等时的国民收入（总产出），也即有效需求，此时国民经济达到均衡。

凯恩斯主义交叉图

计划支出即总需求，实际均衡支出即总供给

2.3消费需求和储蓄

2.3.1 消费函数与消费倾向

• 消费函数(Consumption Function)
  • 线性消费函数：

• 消费倾向(Propensity to Consume)
  • 指消费与收入的比率
  • 平均消费倾向：\(APC=C/Y\)
  • 边际消费倾向：\(MPC\)，就是消费函数的导数
  • \(APC>MPC\)，前者范围为 \(>0\)，后者为 \(0\sim1\)

2.3.2 储蓄函数与储蓄倾向

• 储蓄函数(Saving Function)
  • 线性储蓄函数：

• 储蓄倾向(Propensity to Save)
  • 平均储蓄倾向 \(APS=S/Y\)
  • 同理有边际储蓄倾向 \(MPS\)
    • 当储蓄函数为线性时，MPS为常数1-β
    • 当储蓄函数为非线性时，MPS将随收入增加而增大