产品市场与货币市场共同均衡
3.1 IS 曲线:产品市场均衡
产品市场均衡的条件:总供给 = 总需求
两部门中产品市场均衡的条件:I = S
3.1.1 IS 曲线的数理推导
两部门经济产品市场均衡的三个方程:
- 均衡条件:I﹦S (1)
- 投资函数:I﹦e﹣dr (2)
- 储蓄函数:S﹦﹣α﹢(1﹣β)Y (3)
把(2)式与(3)式代入(1)式, 经整理有:
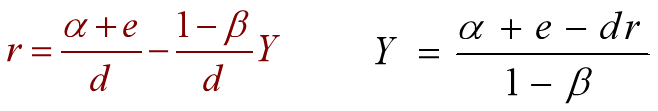
上面两个是等价的,只是不同形式,做计算题时都可以用
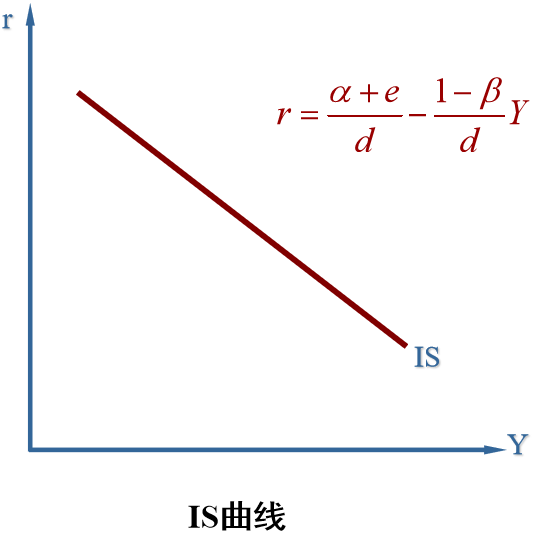
IS 曲线:产品市场均衡时 利率 r 与 国民收入(总产出)Y 的匹配关系。
例题

上面的例题前提是两部门模式,此时 \(I=S\)
但三部门、四部门就不能这样,因为:
- \(Y=C+I+G\)
- \(Y=C+I+G+NX\)
IS 曲线的几何推导(方法二)
有三张图我们都学过,就通过第一张图打两个点,推导至右上张图上两个点在哪,再连线
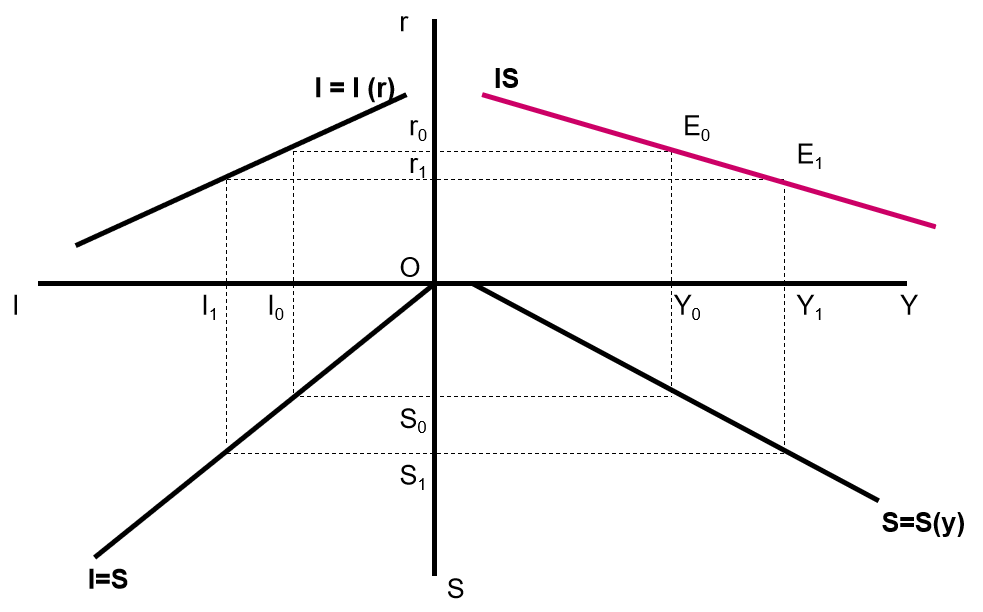
3.1.2 IS 曲线的含义
红线上的点表示产品市场实现均衡,即 I = S,供需平衡
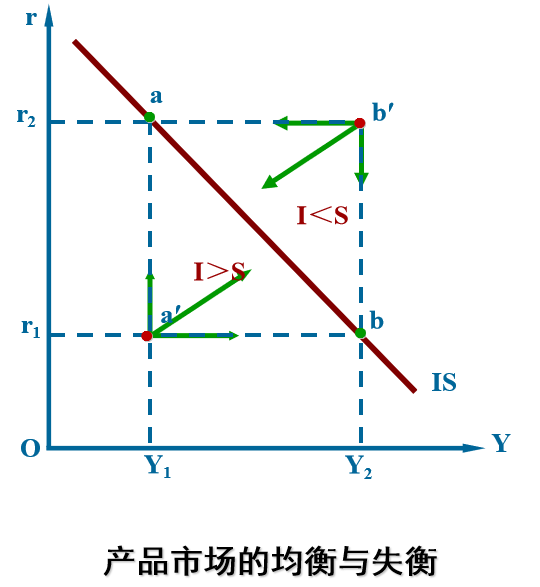
例如,在点 a′,总产出为 Y1(总产出较低因而储蓄较少),利率水平为 r1(利率较低因而投资较大),这就意味着投资大于储蓄,总需求大于总供给,供不应求,刺激 Y 扩张,经济增长,只至点落到红线上,实现平衡
3.1.3 IS 曲线的斜率
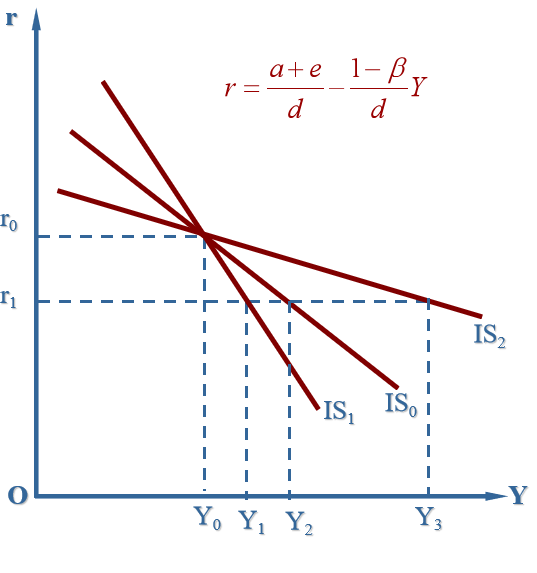
3.1.4 IS 曲线的水平移动
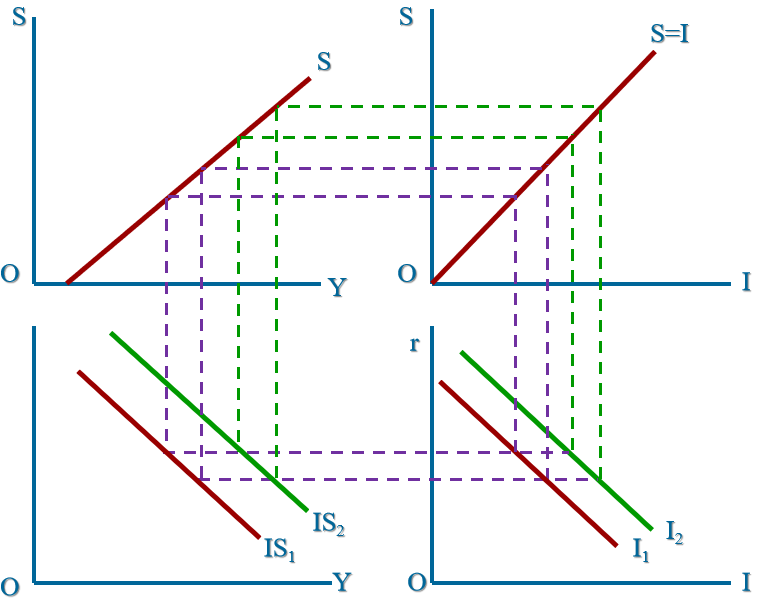
从右下角传到到左下角,得到结论:投资增加-> 总产出增加

从左上角传到到左下角,得到结论:储蓄增加-> 总产出减少
3.2 LM 曲线: 货币市场均衡
货币需求的三大动机:交易动机,预防动机,投机动机
货币需求曲线

交易性货币需求 L1 ,投机性货币需求 L2
货币总需求 L = L1 + L2,即红色曲线
货币需求 L 和货币供给 M 的变动会引起均衡利率的变动。
货币乘数和货币供给
货币供给 = 现金货币+存款货币
如果用 M 表示货币供给,R 表示中央银行发行的现金(即基础货币),r 表示法定准备金率,则:
M = R / r,1 / r 是货币乘数或货币供给乘数
货币乘数是把“双刃的剑”。
法定准备金(Required Reserve Ratio):中央银行对商业银行吸收的存款中所规定的一个最低限度的不得用于放贷的准备金。
法定准备金率:法定准备金占商业银行全部存款的比率。r = R/D,即法定准备金/存款。
3.2.3 LM 曲线的数理推导
货币供给曲线
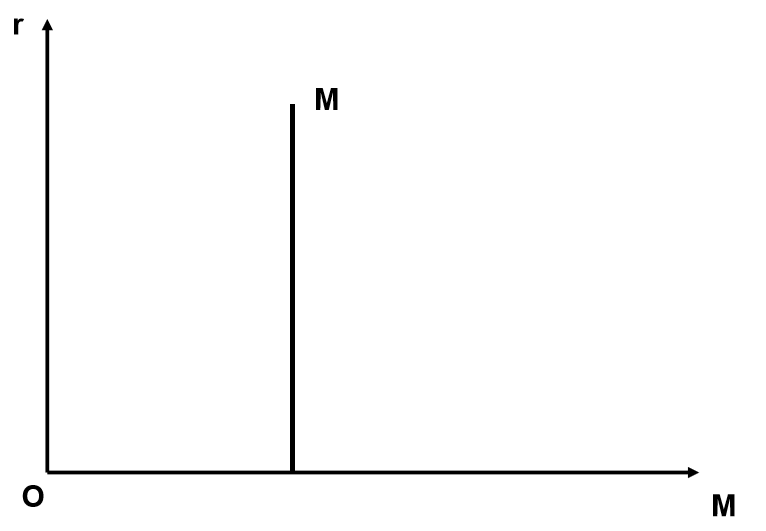
货币市场均衡
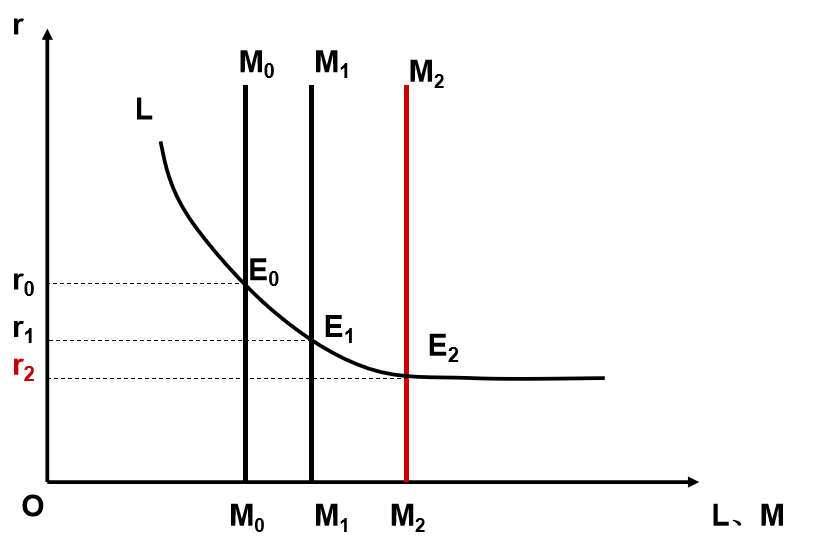
货币市场的均衡的三个方程:
- 均衡条件:L﹦M
- 货币需求:L﹦kY﹣hr
- 前者是 L1,后者是 L2
- 交易性货币需求系数 k 投机性货币需求系数 h
- 货币供给:M ﹦m(设 P = 1)
- 即名义供应量等于实际供应量
得到:

反映货币供需平衡时 Y 与 r 的关系
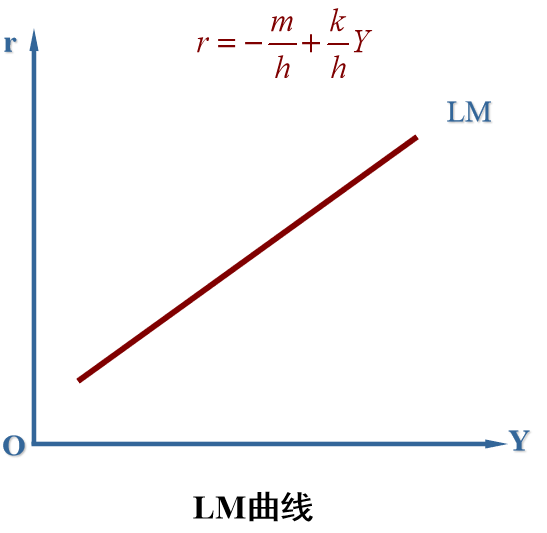
例题

LM 曲线的几何推导
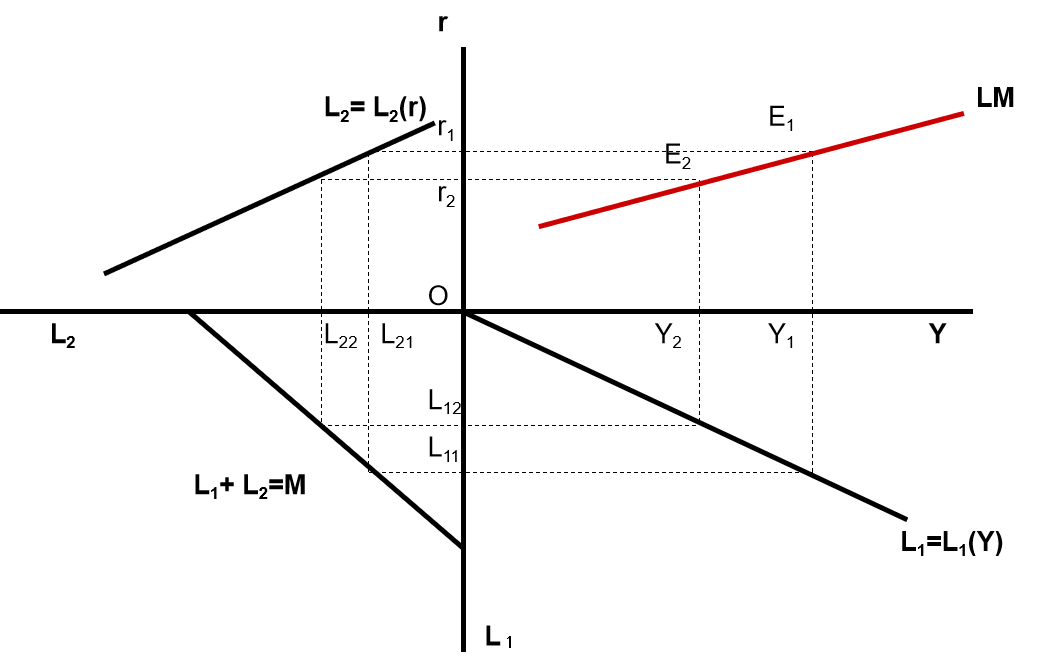
左下角直线表示货币供需平衡
LM 曲线的含义
对货币市场均衡来说,利率与总产出之间存在着正方向变化关系,但二者不是直接的因果关系。
利率 → 投机性货币需求;产出 → 交易性货币需求;
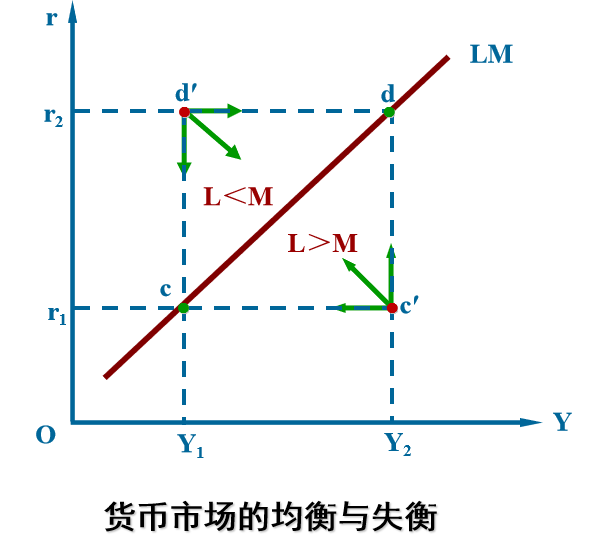
例如,在点 c′,产出为 Y2(产出水平较高因而交易性货币需求较多),利率为 r1(利率水平较低因而投机性货币需求较多),因而总的货币需求大于货币供给。
在 LM 曲线右下方各点都表示货币需求大于货币供给(L > M),在 LM 曲线左上方各点都表示货币需求小于货币供给 (L < M)。
LM 曲线的斜率
LM 曲线的斜率 \(\frac{k}{h}\) 反映产出对利率变动的反应的敏感程度,取决于交易性货币需求系数 k 和投机性货币需求系数 h
LM 曲线的水平移动
交易性货币需求变动,会使 LM 曲线发生同方向移动
投机性货币需求变动,会使 LM 曲线发生反方向移动
货币供给变动,会使 LM 曲线发生同方向移动
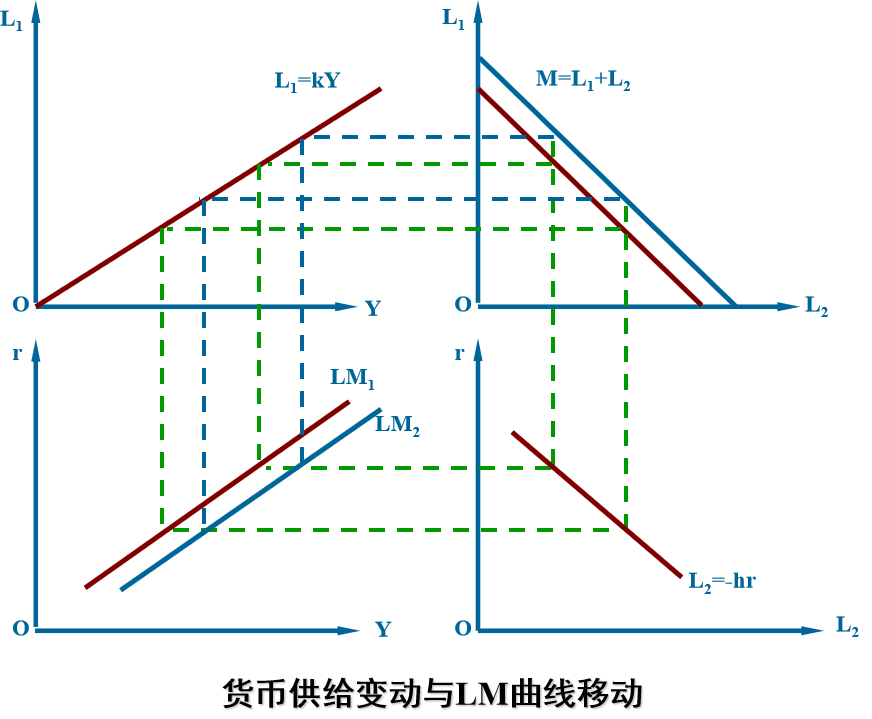
右上到左下
IS-LM 模型: 货币与产品市场同时均衡
IS-LM 模型
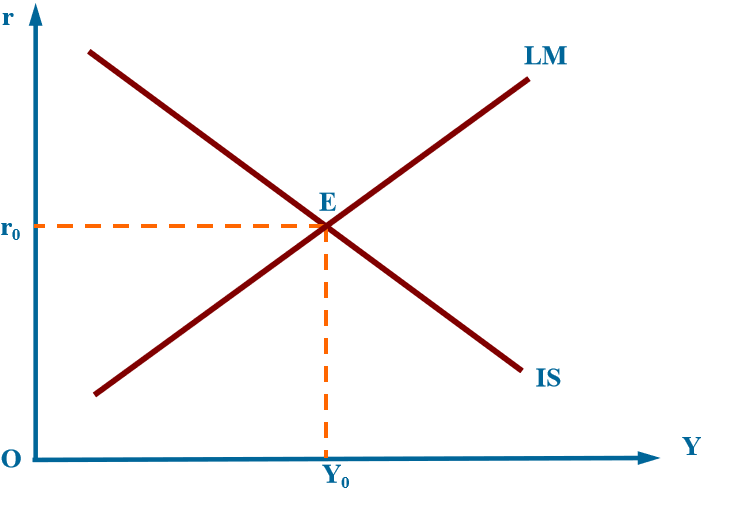
两个市场同时均衡只有一种情况
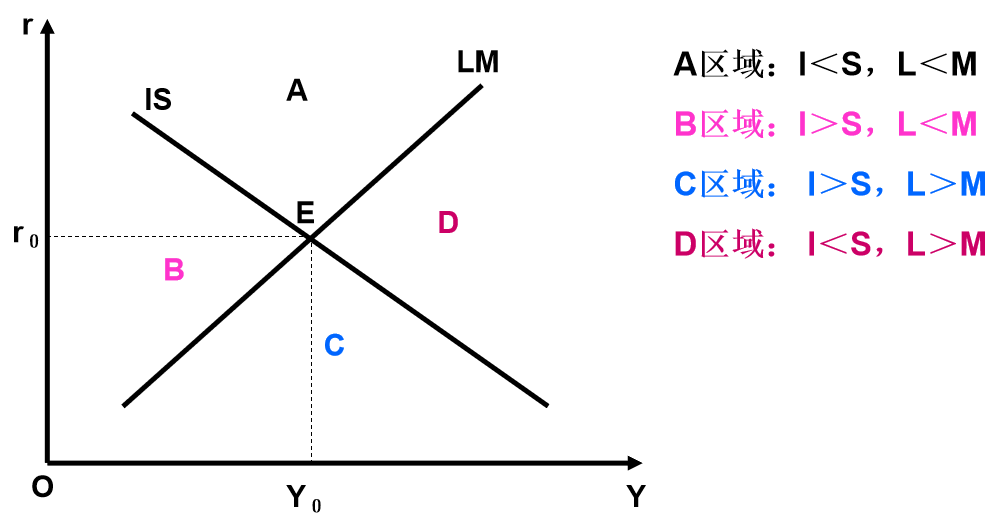
例题

两个市场同时均衡的实现
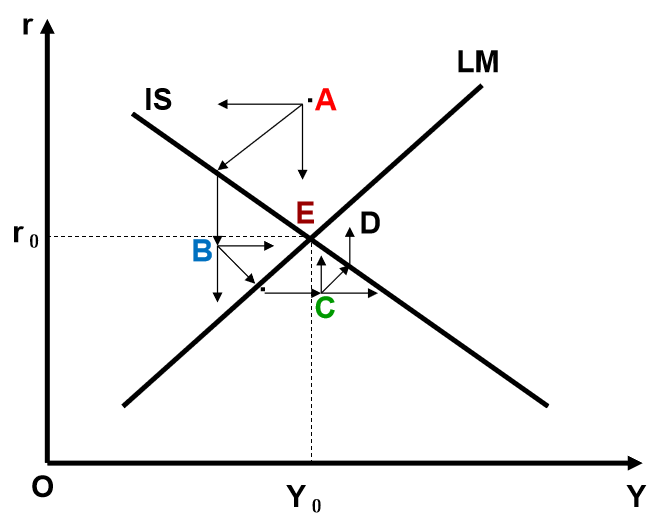
无法一蹴而就,是一级一级地变动
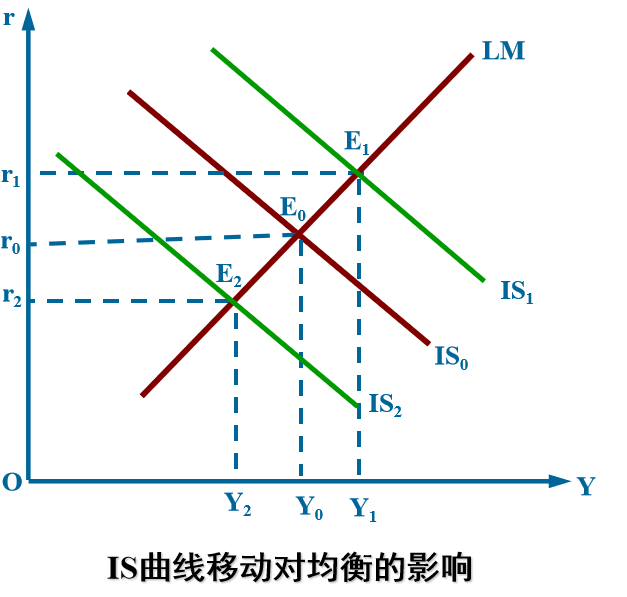
自发支出(如政府投资)增加使IS曲线向右移动,两个市场同时均衡时的总产出增加,利率上升。
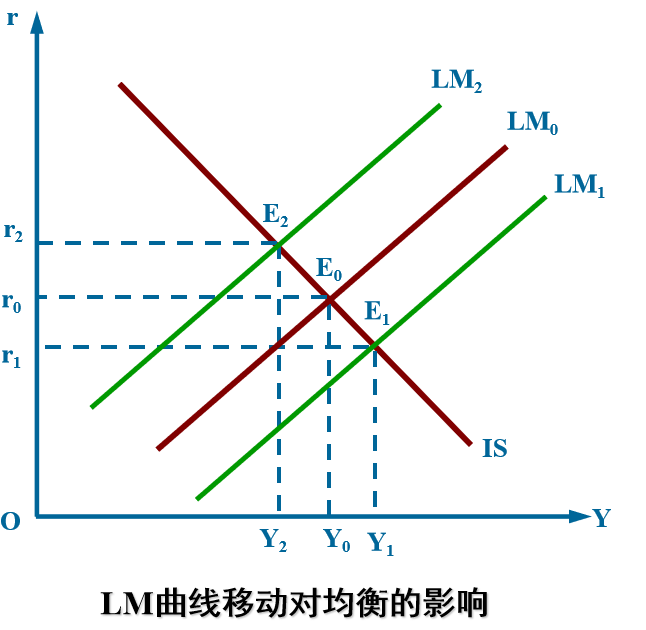
货币供给增加,LM曲线向右移动,两个市场同时均衡时的产出增加,利率下降。
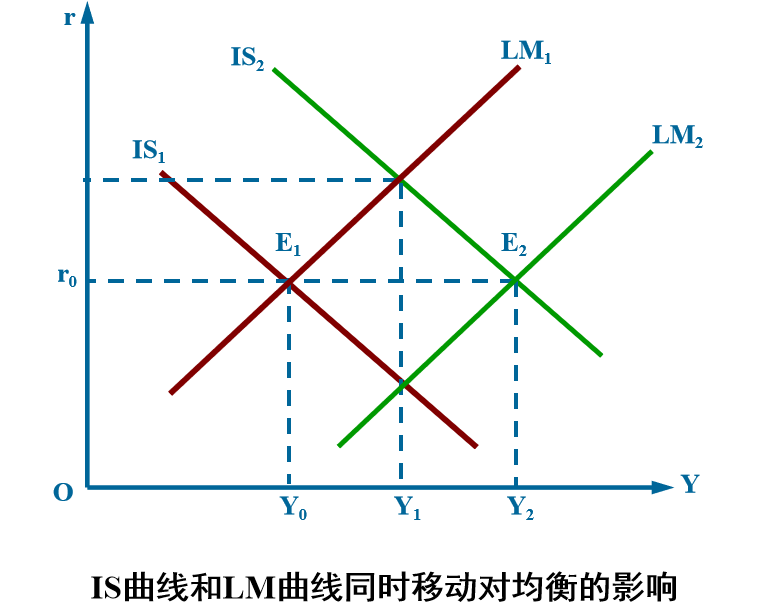
例题


(3)???????????