lec1-intro
NLP 发展历史
规则(机器翻译)--> 概率
- 左派,工程,扩大训练规模
- 右派,仿造人类
机器学习
深度学习包含在机器学习,机器学习包含在人工智能
机器学习 = 寻找一个函数,因为所有人工智能的问题都可以定义为寻找一种函数映射
例如,音频识别即一段音频映射至一段文本,识图即一张图片映射至一段文本
机器学习包含训练(training)和推理(testing)两部分,训练即根据训练数据找出最符合评判标准的参数(函数)
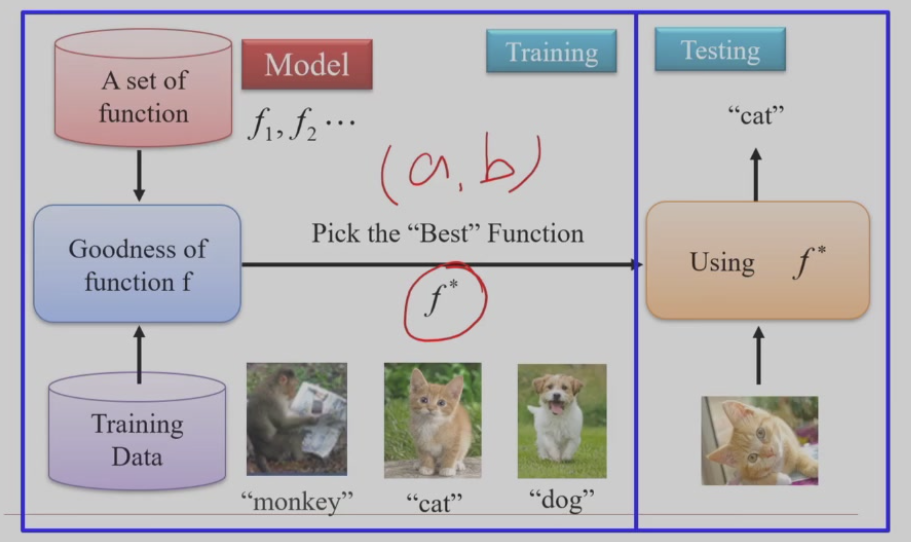
深度学习
神经网络
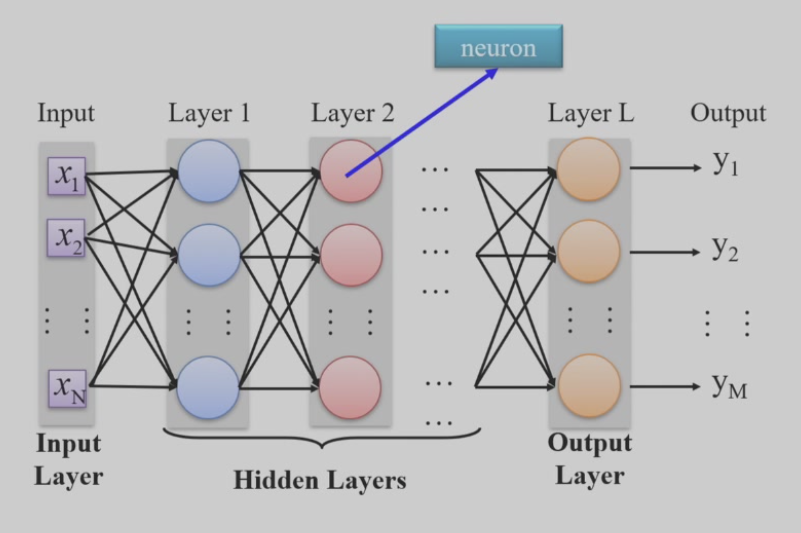
全连接层,每层的神经元都可以收到上一层所有神经元的输入,但同一层之间的神经元互相独立
这种结构容易实现,是最简单的一种神经网络
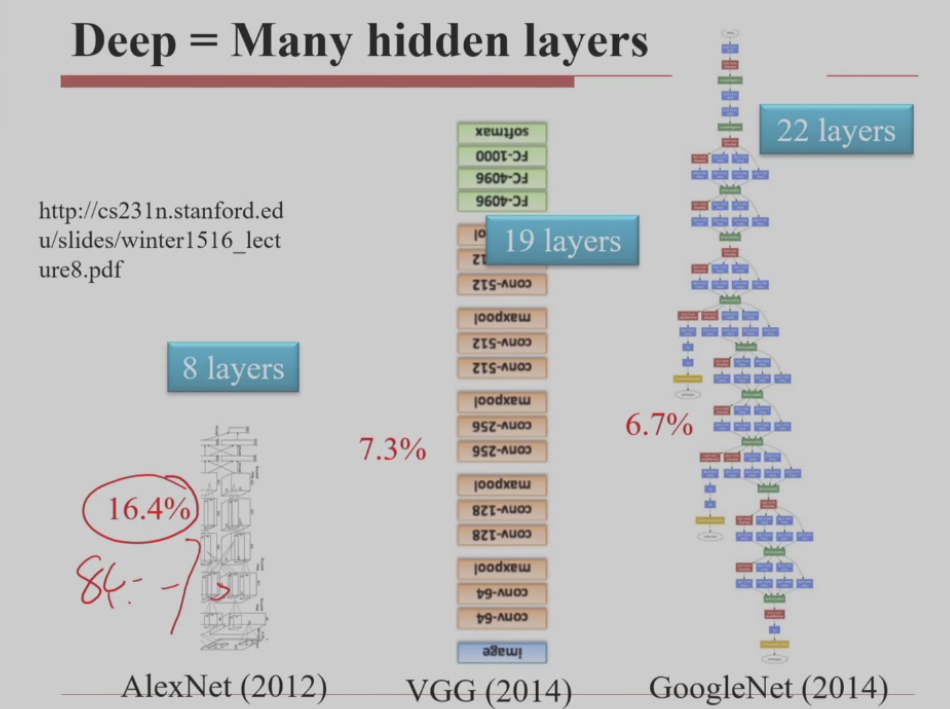
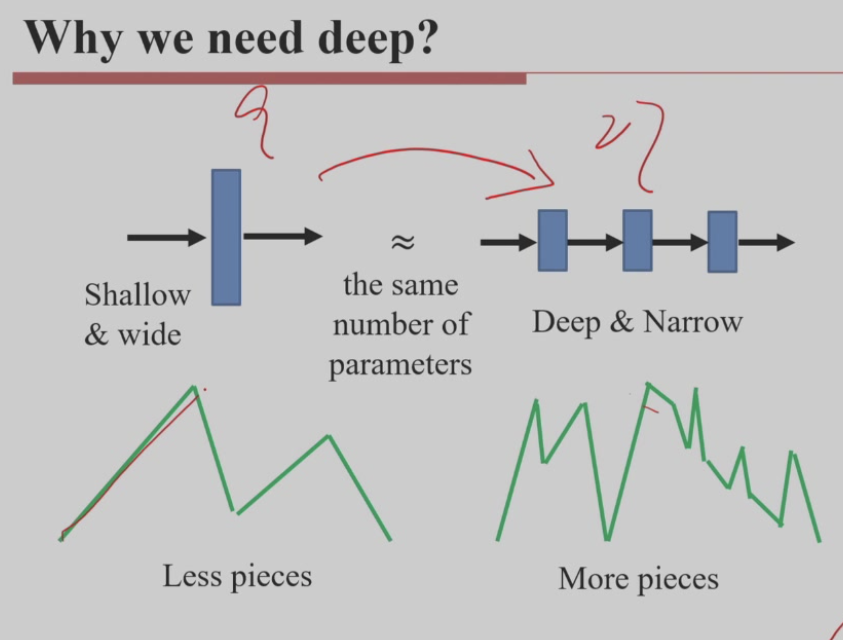
总参数数量相近的情况下,层数多(即“更深”)的网络通常具有更强的表达能力,从而在许多任务上拟合效果更好
当然计算量也增大了
每一层全连接层后通常都会接一个非线性激活函数(如 ReLU、Tanh),多个层堆叠后,整个网络可以表示一个更复杂的非线性函数组合
- 浅层网络能拟合复杂函数,但需要指数级的神经元数量;
- 深层网络可以通过函数复合,更高效地表达复杂函数,以较少的参数构建更复杂的决策边界

训练
训练实际就是找出最好的那一组参数,最好是指能根据输入计算出我们需要的输出。我们一开始只能随便给参数赋值,然后利用数据集训练。
一个问题是如何量化输出的质量,我们引入损失函数,其输入是一组参数,用于计算输入参数下的输出与正确输出之间的差距,显然这个值越小越好。
一个问题是如何更新参数,显然不能穷举,我们可以根据损失函数的值进行更新。损失函数对某个参数的偏导反映了这个参数怎么变化才能让函数值变小,我们可以让参数减去其偏导乘学习率来更新参数。
学习率用于调控参数更新,太大会导致无法达到最优,太小则更新过慢。可先大后小。有专门的优化器用于设置学习率。
这是梯度下降法,无法保证找到局部最优,因为它实际上找的是导数为 0 的点。
神经元
一个神经元会有一组参数与输入进行点乘再相加,这可以看成在做检测,检测输入的趋势是否与参数的趋势一致。假设有四个参数,分别为大小大小,如果输入也为大小大小,输出就能变很大(大小相乘会抵消),相对于这个神经元“选择”了这一种输入组合,否则输出较小,相当于输入被过滤掉了。
随机梯度下降
数据集太大了,算不完,我们每次随机选一部分组成一个 batch 进行训练