Skip to content

lec2-wordembedding

:material-circle-edit-outline: 约 1410 个字 :material-clock-time-two-outline: 预计阅读时间 5 分钟

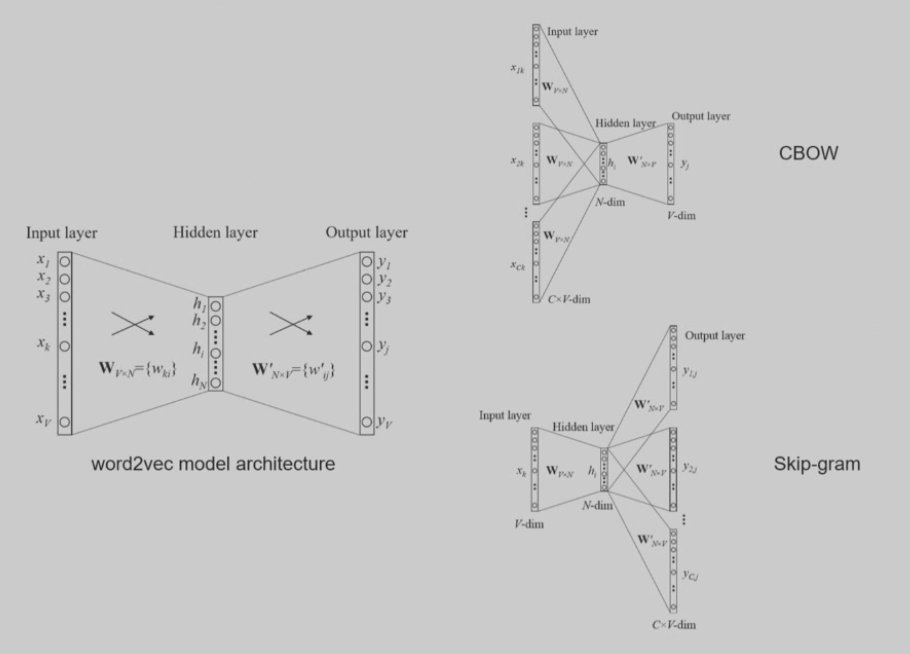
image-20250429232239588

word2vec 结构很简单，以 skip-gram 为例，假设词库有 5 万个词，词向量维度为 300，神经网络有两层，参数分别为 Wi 和 Wo

输入 50000x300 的矩阵，其中将要预测的词的那一行设置为其词向量，其它全为 0，然后得到的输出就是预测得到的词对应的行会有正确的词向量

Hierarchical Softmax

Hierarchical Softmax（层次 Softmax）是一种 高效替代传统 Softmax 的方法，常用于词向量训练（如 Word2Vec）或需要在 大词表中做分类 的任务。它的核心思想是：将所有类别（如单词）组织成一棵树，使得每次预测的时间复杂度从 O(V)O(V) 降低到 O(log⁡V)O(\log V)。

🧠 问题背景：普通 Softmax 有多慢？

在标准的 Softmax 中，给定词表大小 VV（例如 10 万个词），我们在输出层需要做：

  • 每个词计算一个得分（点积）；
  • 再用 Softmax 转成概率分布。

这会导致时间复杂度是 O(V)O(V)，对于大词表非常慢！

🌲 Hierarchical Softmax 的核心思想

将 Softmax 变成“走一棵二叉树”的过程，每次分类不再是对所有词做归一化，而是从根节点一步步走到目标词节点。

  • 整个词表组织成一棵二叉树（通常是霍夫曼树）；
  • 每个词是树的一个 叶子节点；
  • 要预测一个词，只需判断“从根走到这个词的路径上每个节点的左/右方向”；
  • 每次决策是一个 二分类 问题（走左还是右）；
  • 每个路径长度是 O(log⁡V)O(\log V)，所以整个预测时间也降到 O(log⁡V)O(\log V)。

🔢 举个简单例子

假设词表有 8 个词，用一棵二叉树组织如下：

          o
         / \
       o     o
      / \   / \
     a  b  c   d

若你想预测词 a，只需走路径：左 → 左 你不需要计算其他词的概率。

💡 每个内部节点都有自己的参数

  • 每个内部节点都有一个参数向量 vn\mathbf{v}_n；
  • 给定输入向量 h\mathbf{h}，每一步的概率是：

P(走左 ∣h)= σ(vn⊤h)P(\text{走左} | \mathbf{h}) = \sigma(\mathbf{v}_n^\top \mathbf{h})

整条路径上的概率就是每个决策概率的连乘：

P(词 ∣h)= ∏j = 1LP(走左或右 j∣h)P(\text{词} \mid \mathbf{h}) = \prod_{j = 1}^{L} P(\text{走左或右}_j \mid \mathbf{h})

✅ 优点

优点 说明
计算更快 时间复杂度从 O(V)O(V) 降为 O(log⁡V)O(\log V)
更适合大词表场景 如 Word2Vec、语言建模
可以避免负采样（某些任务）

⚠️ 缺点

  • 实现比普通 Softmax 更复杂；
  • 性能与树结构有关（如果树不平衡，会影响效率和效果）；
  • 不适合要求“预测所有类别概率分布”的场景（因为它只能高效地预测 某一个目标词）。

总结一句话：

Hierarchical Softmax 把“对所有词分类”变成了“走一棵树的一条路径”，大大提高了效率，非常适合大词表场景。

你是在哪个模型中遇到 Hierarchical Softmax 的？是 Word2Vec、RNN 还是 Transformer 的应用？我可以根据你具体的模型讲得更贴近。

Negative Sampling

负采样（Negative Sampling）是用于加速模型训练（尤其是 Word2Vec 中 Skip-gram 模型）的一个近似优化方法。它的核心思想是：

不用对整个词表做 Softmax，而是只区分“正确词（正样本）”和“随机词（负样本）”，转化为一组二分类问题。

🧠 背景：为什么需要负采样？

在 Word2Vec 的 Skip-gram 模型中，我们要最大化：

\(P(\text{上下文词} \mid \text{中心词})\)

如果用标准的 Softmax，要遍历整个词表（可能有几十万词），计算代价很高。

🚀 负采样的核心想法

训练目标转化为：

  • 对一个 中心词 + 上下文词对（正样本），让模型输出概率接近 1；
  • 对一些 中心词 + 随机词对（负样本），让模型输出概率接近 0；
  • 换句话说：只优化一小部分词，而不是整个词表。

这就大大减少了计算量。

🔢 损失函数（逻辑回归形式）

给定中心词向量 \(\mathbf{v}_c\)，上下文词向量 \(\mathbf{v}_w\)，负样本集合 \(\{w_1^-, w_2^-, \dots, w_k^- \}\)，损失函数为：

\(\log \sigma(\mathbf{v}_w^\top \mathbf{v}_c) + \sum_{i = 1}^k \log \sigma(-\mathbf{v}_{w_i^-}^\top \mathbf{v}_c)\)

  • 第一项鼓励正样本点积大（概率接近 1）
  • 后面几项鼓励负样本点积小（概率接近 0）
  • \(\sigma\) 是 Sigmoid 函数

✅ 优点

优点 说明
计算效率高 不需要对整个词表做 Softmax，速度提升巨大
简单易实现 本质是多个二分类问题
效果好 实际训练中表现非常好，是 Word2Vec 默认做法

⚠️ 负采样的注意点

  1. 负样本数量（k）选择：

    • 通常取 5~20；
    • 太少会欠拟合，太多会影响效率。

  2. 负样本如何采样？

    • 常用“按词频开 3/4 次方”作为采样概率：

      \(P(w) \propto f(w)^{3/4}\)

    • 这样既不会选太多高频词，也不会完全忽视它们。

✅ 总结一句话：

负采样通过转化为多个二分类问题，避免对大词表做全量 Softmax，从而大幅加快模型训练速度，是 Word2Vec 和一些语言模型中的重要技术。

是否需要我结合代码或图示，演示它和 Softmax 的区别？或者你想了解它在其他模型中的应用（比如负采样在图神经网络中的用法）？

词向量局限

  1. 无法处理一词多义
  2. 难以调试
  3. 忽略了顺序信息