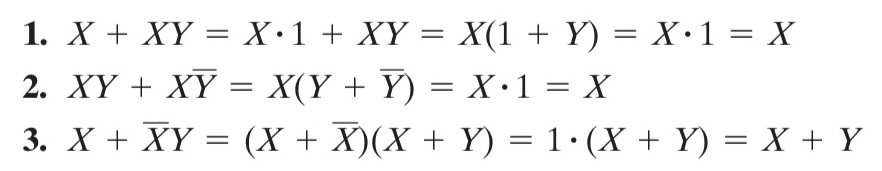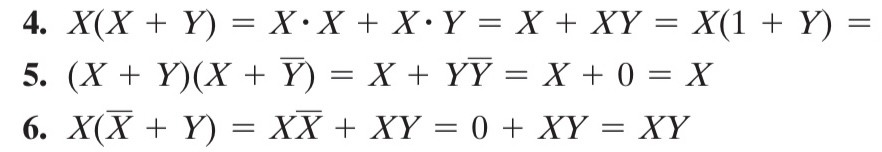注意

下面的内容其实就是修佬的笔记cv过来的，只是根据个人的情况进行了内容筛选，加了几行个人用的注释，所以没必要往下看了，放这里是个人复习用的。直接去看原版，修佬yyds——💎 数字逻辑设计 | Digital Design - Isshiki修's Notebook (isshikih.top)

Chap 1 Digital Systems and Information

:material-circle-edit-outline: 约 19771 个字 :material-clock-time-two-outline: 预计阅读时间 66 分钟

信息表达 | Information Representation

现实世界中的信息往往是 连续(continuous) 的。

但在人造物的世界中，大部分信息都是 离散(discrete) 的。

在电子信息系统中，信号分为 模拟信号(analog signal) 和 数字信号(digital signal) 两种。

在 数字信号(digital signal) 中又有多种表示方法，如今我们最常用的是 二进制(binary)。对应到电路层面，我们常常用 高电位(HIGH) 和 低电位(LOW) 来表征 1 和 0。

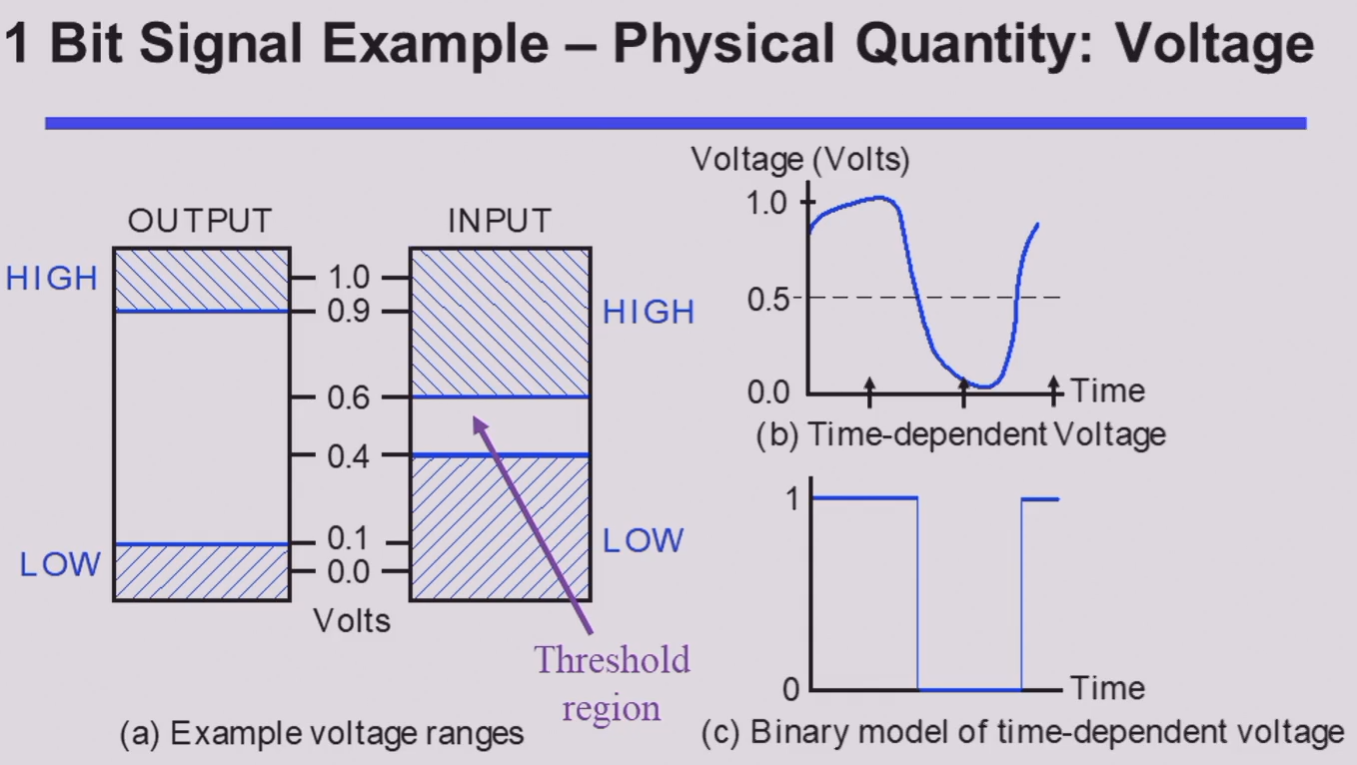
值得注意的是，在输入和输出中，高低电位的接受范围是不同的。

可以发现，输入的判定范围比输出的判定范围大，即 宽进严出。

其目的是为了进一步提高电路在噪音等异常影响下也能正常表现的能力。

HIGH 的接受范围和 LOW 的接受范围之间还存在一段区域。落在这一部分的电平是 未定义(undefined) 的，也被称为是 浮动(floating) 的。

如果输出的电平是在浮动区间的，那么其认定值将是随机的。

事实上，在信息的对应上，虽然将高低电平同 HIGH/LOW 联系是很自然的，但是将他们同 true/false 或者 1/0 联系其实并不唯一。但是在一般情况下（我们称之为 positive logic），我们都认为 HIGH ~ true ~ 1， LOW ~ false ~ 0。

可以发现，(b) 图中的模拟信号在经过我们的器件后，会被认为是 (c) 图所示的信号。而这些操作在硬件层面，我们通过 晶体管(transistors) 来实现。

这也牵扯到我们为什么最终使用二进制来表示信息。一方面是因为二值器件比较常见，亦即这里提到的晶体管；另外一方面是使用二进制可以降低电路成本。

计算机系统设计中的抽象层 | Abstraction Layers in Computer Systems Design

越上层抽象程度越高
Algorithms
Programing Languages
Operating Systems
Instruction Set Architecture
Microarchitecture
Register Transfers
Logic Gates
Transistor Circuits

数字系统 | Number Systems

进制转换

对于一个 $r$ 进制数，它一般被写成这样：

而它对应的十进制真值为：

计算机领域常见的进制主要是 二进制(binary)，八进制(octal)，十进制(decimal) 和 十六进制(hexadecimal)。

其中二、八、十六进制之间的转换非常简单，存在多位到一位之间的无后效性映射，例如二进制转换到十六进制只需要将从低到高每四位转化成十六进制中的一位即可。

需要注意，由于二进制和十进制在零位上的权重相同，这意味着在整数部分，二进制和十进制是可以相互精准转化的（即最小精度是一致的，都是 1）；

然而该性质在小数部分并不成立（因为小数部分不存在“最小精度”一说），即十进制无法精准转化为二进制，但二进制可以转化为十进制。

算术运算 | Arithmetic Operations

这里涉及的主要是 加法(Addition)、减法(Subtraction)、乘法(Multiplication)。

编码 | Codes

二进制编码主要分为这么几种：

Numeric
- 必须表达一定范围内的数字；
- 能够支持简单且普遍的计算；
- 和二进制数值本身有较大关联；
Non-numeric
- 相对灵活，因为不需要适配普遍的运算法则；
  - 灵活是指，保证编码映射关系是唯一的的情况下都可以称为合法编码；
- 和二进制数值本身未必有关系；

独热码 & 独冷码

独热码(one-hot) 要求比特向量中只有一位是 1；对应的还有 独冷码(one-cold)。

使用这种编码的好处是，决定或改变状态机目前的状态的成本相对较低，容易设计也容易检测非法行为等。

但是相对应的，缺点是信息表示率较低，非法状态非常多而有效状态很少。

BCD 码

真实世界中大部分数据表述都是以十进制实现的，所以我们需要研究如何用二进制来表示十进制。

一位二进制数能包含的信息是 1bit，也就是一个“真”或者一个“假”。

我们称一个拥有 n 个元素的二进制向量为一个 n位二进制编码(n-bit binary code)。一个 n 位二进制数拥有 $2^{2n}$ 种可能的组合，因而可以表示 $2^{2n}$ 种信息。

我们需要设计的编码系统，就是将我们需要的信息映射到这 $2^{2n}$ 个“空位”中。当然，当我们需要表示的信息数量并不是 2 的幂次时候，会出现一些未分配(unassigned) 的比特组合。

在这种编码中，最常用的就是 BCD码(binary-coded demical)。其核心思路就是，将十进制的每一位分别用 真值相等的 4 位二进制 表示，即 0 ~ 9 分别用 0000 ~ 1001 表示。

eg

$(185)_{10}=(000110000101)_{BCD}=(10111001)_2$

余三码

一种 BCD码 的改进是 余三码(Excess3)。

其核心思路是在 BCD码的基础上，增加一个大小为 3 的偏移量，即每个二进制编码＋3。

这个 3 来自于 $\frac{16-10}{2}$ ，也就是 8421 码的容量减去我们需要表示的数字数量，再除以二。

这样的好处是，十进制下能进位的两个数，在余三码下相加也刚好进位。

格雷码

格雷码的特征，也是他的优点，就是相邻的两个数在二进制下的表示只差一位（当在占满时，对于整个编码序列，环状满足该条件）。

从笔试做题角度来说，格雷码最麻烦的其实是与十进制数的转换。

假设我们要找的是第 k 个格雷码，则对应的格雷码为：

ASCII 码

字符编码所使用的一般是 ASCII 编码

奇偶校验位

在信号传输过程中，可能由于环境干扰等原因，出现各种信号抖动，所以为了保证数据的可信度，我们需要一个错误检测机制。

一种常见的方法是 冗余(Redundancy)，即加入一些额外的信息用以校验。

其中一种做法是引入 奇偶校验位(Parity Bit)。它分为 奇校验(Odd Parity) 和 偶校验(Even Parity)。

分别通过引入额外的一位，来保证整个信息串中 1 的数量是奇数/偶数。

比如，如果我们采用偶校验，原始信息为 1101，其中有 3 个 1，这时我们在后面再加上一个 1，保证了整个信息串中有偶数个 1；
或者如果原始信息为 1001，其中有 2 个 1，这时我们则在后面加一个 0。此时，如果传输过程中出现了问题，那么 1 的数量很可能变成了一个奇数，此时我们就知道，这个信息是不对的。

Chap 2 Combinational Logic Circuits

逻辑运算

逻辑运算的对象是布尔变量，也就是 0/1 二值。

主要的运算就是 与(AND)，或(OR)，非(NOT)，异或(XOR)，以及 与非(NAND)，或非(NOR)，同或(XNOR)。

多输入的异或和同或被称为奇函数和偶函数。

可以用它们来实现奇校验和偶校验。

而且观察其卡诺图的形状（棋盘形），可以发现，它们是天然优化的，即不可优化的。

NOR: $\overline{A+B}$
NAND: $ \overline{A\cdot B}$

德·摩根定律(De Morgan's Laws)

$\overline{A+B}=\overline{A} \cdot \overline{B}$
$\overline{A\cdot B} = \overline A+\overline B$

逻辑门

逻辑门是在硬件层面上实现布尔代数的逻辑单元。其操作对象为高低电平。

通用门(Universal Gate)

一个功能完全的，能够表示其他所有门的逻辑门被称为通用门。

在我们学过的逻辑门中，NAND 和 NOR 都是通用门。

布尔代数

literal ~ 字面量，也就是“变量”。

运算律

主要注意第15条

一定要建立与和或是对等的观念

我们习惯用“真”去理解这两个运算，但是实际上如果你以“假”为主体去分析这两个运算，会发现和“真”是完全对称的。换言之，与和或是完全对称的运算，而非像他们借用的符号 × 和 + 那样存在非对称关系。

但是让这件事变得又没那么简单的事情是，虽然与和或是对等的，但是我们在借用普通代数符号体系的同时，又人为地给他们添加了优先级（但是这也是必要的，否则表达式就会充满括号）。

运算律推广

对比前三个和后三个，我们再次发现，与和或在逻辑上是对称的。

对偶法则

对偶法则(Duality Rule)：一个表达式的 对偶(dual) 为，将所有的与和或对调得到的式子

注意：需要保证参与运算的结构不能变（是“带括号”的宏展开）。

eg

一般情况下，除非某个表达式是 自对偶(self-dual) 的，那么它的表现都与原表达式不同。

对偶表达式具有如下性质：

如果 F 的对偶是 G，那么 F 也是 G 的对偶，即对偶关系是对成的；
如果表达式 F 和 G 等价，那么他们的对偶也等价；

互补函数

一个 函数的互补(Complement of a Function) 指的是，将它的 对偶函数 中每一个变量都取反得到的函数，而该函数正好等于原函数的非。

eg

替代法则

替代法则(Substitution Rules): 如果将一个等式中 所有的 某个变量 都替换为同一个表达式，则等式依然成立。

eg

一致性定理

\[ XY+\overline XZ+YZ=XY+\overline XZ \]

证明：利用 $YZ=(X+\overline X)YZ$

标准形式与规范形式

本质上相等的布尔表达式实际上有很多种写法。

随着变量越来越复杂，他们之间的比较会很困难。

所以我们需要定义一种形式，使得所有相同的表达式都能比较方便的“化简”为同一个形式，同时也能辨别出两个表达式是不同的。

这就引入了 标准形式(Standard Forms)，包括 SOP 和 POS；以及 规范形式(Canonical Forms)，分别为 最小项之和(Sum of Minterms, SOM) 和 最大项之积(Product of Maxterms, POM)。

表达规范

\[ SOM\\ F(X,Y,Z)=\sum m(2,4,5,7)=m_2+m_4+m_5+m_7 \]

$\sum m$ and $m\ subscript$ 数字的二进制对应着最小项

$$ POM\ F(X,Y,Z)=\prod M(0,1,3,6)=M_0+M_1+M_3+M_6 $$

$\prod M$ and $M\ subscript$ 数字的二进制反码对应着最大项

对于一个二值表达式来说，两种表达都是充要。

最小项与最大项求反可得到同一下标的对方
- 可知 $F$ 的 $SOM$ 下标与其反函数的 $POM$ 下标一样

电路实现与优化

直接通过标准形式来得到对应的电路会导致成本过高以及电路复杂

通过 卡诺图(Karnaugh map) 来优化逻辑电路

我们需要先定义什么是“优”，也就是给出一个电路成本的衡量依据，即 成本标准(cost criteria)

成本标准

在成本标准中，我们需要介绍的主要有三种标准，分别是：

按照字面量字面量计(literal cost)：$L$
按门输入计，不计非门(gate-input cost)：$G$
按门输入计，计非门(gate-input cost with NOTs)：$GN$

按照字面量字面量计

就是按照表达式中有多少字面量来计算，即有多少个字母

eg

这种计算方法非常的简单，但是感觉不太靠谱

按门输入计

按照逻辑门输入引脚的总个数来计算

这里的输入并不仅仅是直接来自于字面量输入的那些引脚，也包括字面量做运算后得到的结果作为输入传入下一级逻辑门的引脚

⚠ 注意

虽然非门也是门，但是我们通常不把非门直接计入 gate-input cost，所以接下来提到的“输入引脚”默认是不包含非门的输入引脚的。

eg

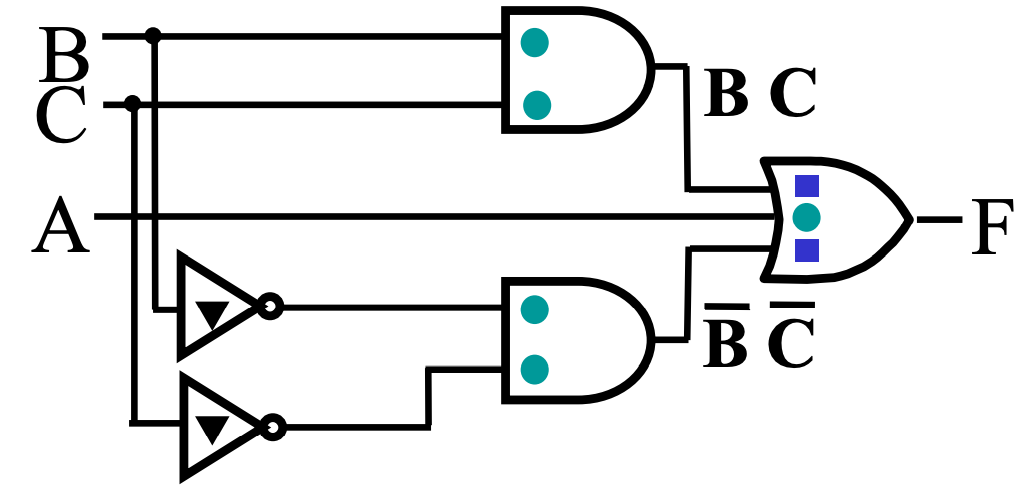
绿色原点表示一级输入引脚；
蓝色方点表示二级输入引脚；
黑色三角表示非门的输入引脚

也就是说，这里一共有 5 + 2 = 7 个输入引脚，以及 2 个非门输入引脚。

出现了重复的被非了的字面量，不要重复计算

更多例题（考前做做练手）

Chap 2 Combinational Logic Circuits - Isshiki修's Notebook (isshikih.top)

注意：分层计数。对于一项，分为输入与输出分别计数！！！！！！！！！

顶层的输出不计

这里还不熟练，可能会做错

卡诺图

优化逻辑表达式最直白的思想就是减少门电路，也就是去减少 gate-input cost。

如果两个最小项只差一个字面量的非，那么他们是可以合并的。这个结论对最大项也成立。 $$ XY+X\overline Y=X(Y+\overline Y)\ (X+\overline Y)(X+Y)=X+Y\overline Y=X $$ 是不是觉得“只差一个”很耳熟？是的！我们想到了格雷码！

假设我们将 n 个字面量排列成一个 n bits 的向量，那么只需要按照格雷码排序，一旦发现有相邻的最小项，我们就可以合并他们。

但这还不够充分，例如在一个有三个字面量的逻辑表达式中，“与一个表达式相邻”的表达式其实有三个，但是用线性的表示方法又没法很好的表示这一点。

所以我们想到将它写成一张二维的表，即将字面量拆成两组 bit 向量，各自按照格雷码排列，形成一张二维表，这就是 卡诺图(Karnaugh Map)，也叫 K-map。

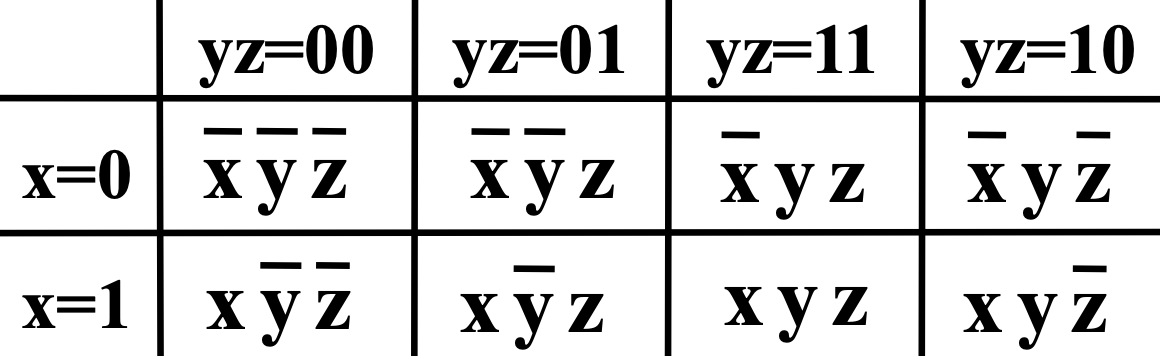
可以发现，任意两个相邻的格子都只差一个字面量的非，而且是充要的，即所有“相邻”都可以在这张图表现出来。

由于格雷码的性质是一个在“满”状态下 环状成立 的性质，所以卡诺图也需要用“环状”的思路去看，这里可以联想一下行列式的形象化计算方法，将这张表当作一个无限扩展的表格。

卡诺图的局限性

一张二维表中，能与一个元素相邻的元素最多只有四个，也就是说我们撑死也只能用卡诺图表示 4 个字面量的情况。

实际上卡诺图只能用于化简非常简单的逻辑表达式。

更多情况下，卡诺图实际上只适合我们做题。但是其思路是非常有意思的。

卡诺图的结构

3 bit

[x, y, z] --> [x], [y, z]

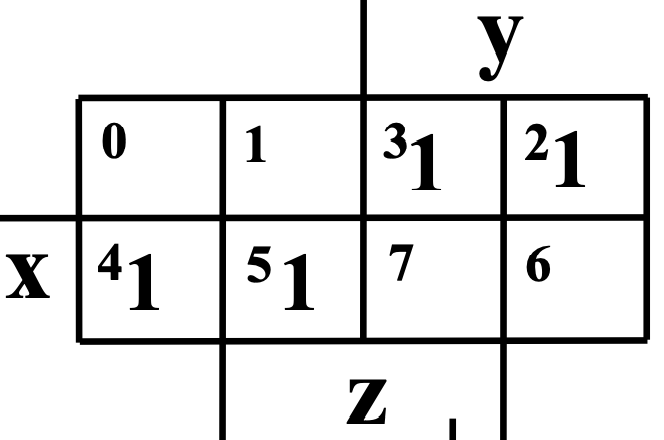
4 bit

[w, x, y, z] --> [w, x], [y, z]

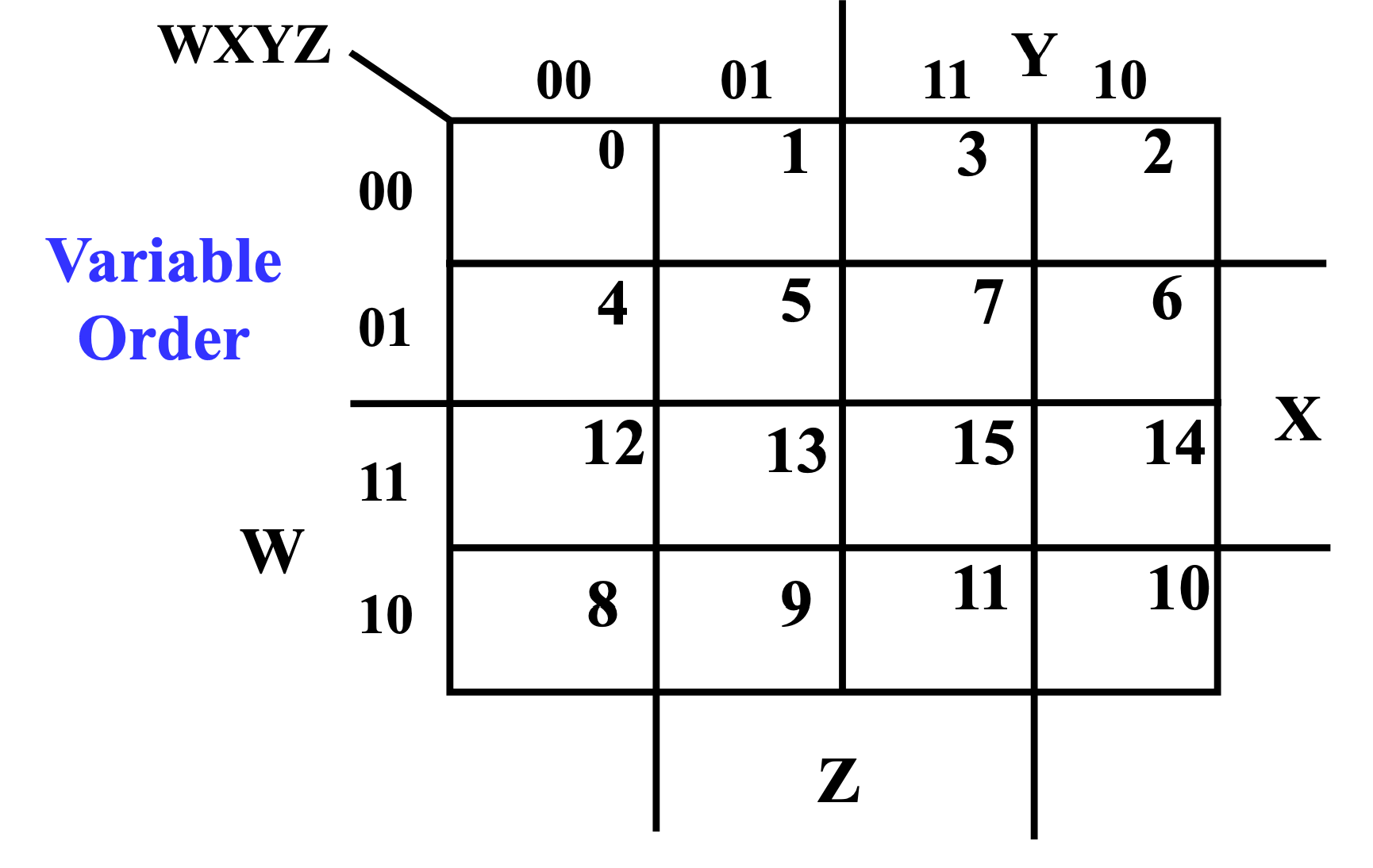
卡诺图里最小项标1，最大项标0

不定项

不定项(Don't Cares) 指的是需要化简的逻辑函数中，没有给出定义的几项，它们可能是：

输入组合不会出现；
输入组合的输出不被使用；

对于这种项，在卡诺图中用 X 来表示，在最小项之和中用 $\sum d(...)$ 表示。

我们可以随意定义它们的输出，此时就可以利用这些项来方便我们的优化——当我们画出来的极大矩阵越大，成本就越低。

由卡诺图得到乘积结果

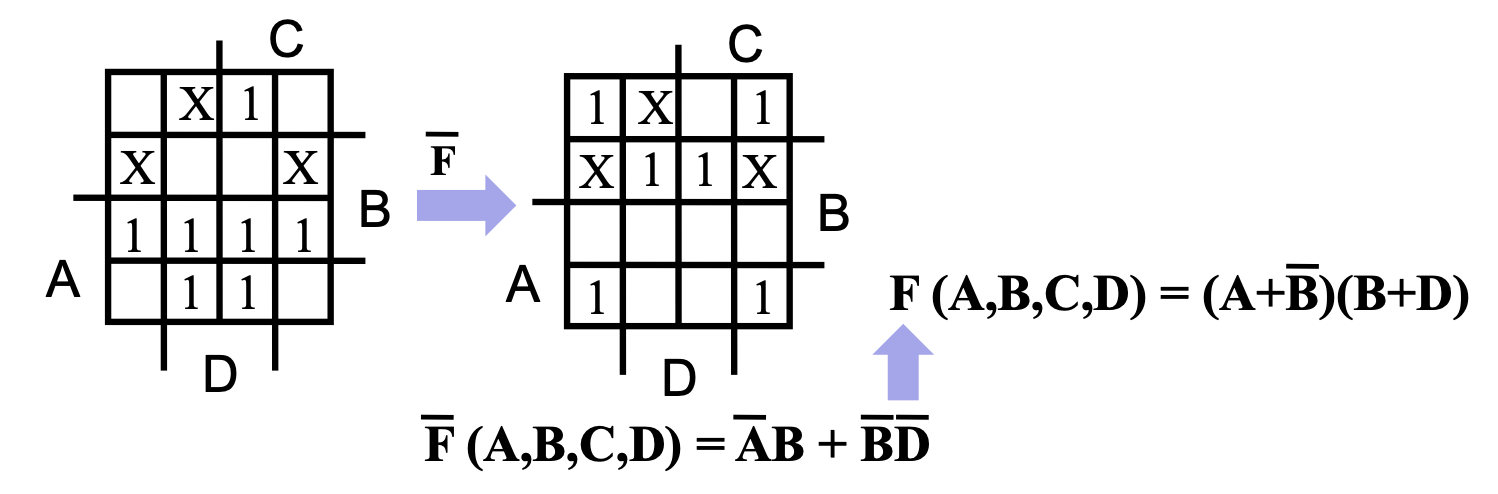
尽管我们不停强调与和或是对称的，但是仍然有很多操作是鉴于我们对 1 的偏爱才会顺手的

在卡诺图的问题中，如果要利用卡诺图得到 $F$ 优化后的乘积形式，也可以将问题转化为求 $\overline F$ 优化后的和形式，然后再对其取反，利用德·摩根定律来得到结果。

具体来说就是反转 K-map 中所有的 0 和 1，然后着眼于 SOM 进行优化，最后再对结果取反，用德·摩根定律来得到结果。

eg

蕴含项、主蕴含项与基本主蕴含项

蕴含项(implicant) 分为 主蕴含项(prime implicant) 和 基本主蕴含项(essential prime implicant)。

在卡诺图中，一个蕴含项就是任意一个包含 $2^n$ 个 1 的单元；
主蕴含项则是在卡诺图中的极大蕴含项；
- 对于存在 Dont'cares 的 K-map，如果我们关注的是 1，那我们积极地将他们当作 1 来处理，反之亦然；
- 但是单独的 X 不会被认为是主蕴含项；
基本主蕴含项是包含只被它(基本主蕴含项)覆盖的 1 的主蕴含项；

⚠ 对于任意函数，主蕴含项一定存在，但是基本主蕴含项不一定存在。

introduction

按照功能，逻辑电路分为两类：

组合电路(Combinational Circuit)

拥有 m 个输入和 n 个输出，其中包含了 $2^{2m}$ 种输入组合，以及对应的 n 个不同的函数；

最关键的是，它的 输出只依赖于这 m 个输入的组合（不包含回路）；

时序电路(Sequential Logic Cirtuit)

与之对应的，时序电路具有记忆功能，即它的输出可能会依赖之前的结果；

Chap3 Combinational Logic Design

Chap 1 Digital Systems and Information
Chap 2 Combinational Logic Circuits
Chap3 Combinational Logic Design
！！延迟计算
Chap3 组合逻辑 coder+multiplexer
- 基本逻辑函数
- 基本功能块
Chap3 算术逻辑电路
- 半加器 & 全加器
  - 半加器
  - 全加器
- 行波加法器
！！超前进位加法器
- 二进制减法
  - 无符号减法
！！有符号数的表示与计算
Chap-4 Sequential Circuits
Chap5 Digital Hardware Implementation
- 设计空间
  - 集成电路¶
  - CMOS
- 可编程技术
  - 常见的可编程技术
    - ROM
    - PAL
    - PLA
  - Lookup Tables（查找表 LUT）
    - CLB
    - SM
    - IOB
Chap 6 Registers & Register Transfers
Chap7 存储器
- Memories
  - Memory Organization
- RAM
  - SRAM
  - Operations
    - Write
    - Read
- Word
- Communication
- Size
- eg

表示逻辑的方法

真值表(Truth Table)；
布尔函数(Boolean Function)；
卡诺图(Karnaugh Maps)；
时序图(Timing Diagram)；
逻辑电路图(Logic Circuit)；

其中，加粗的方法功能确定的情况下，其表示是唯一的。

设计流程(Design Procedure)

说明：确定系统的行为，用文本或HDL
配置：述输入和输出之间的逻辑关系，并用真值表或逻辑表达式表达出来
优化：优化逻辑表达以减少成本(比如使用卡诺图)
映射(Technology Mapping)：将优化后的逻辑设计工艺映射到硬件实现上（如用logisim画图）
验证：验证正确性（在仿真环境中）

分层设计(Hierarchical Design)

内容：将复杂问题模块化分解为若干层次，然后逐个抽象解决
方法
- Top-down: 将电路拆分成小模块(block)，将小模块拆成更小的模块
  - What are we building?(从需求出发) + controls complexity
- Bottom-up: 将 primitive block 组装成需要的模块
  - How do we build it?(根据现有的元件去组合成目标功能) + focuses on the details
- 无法继续拆分的模块叫 primitive block
- 所有的模块——包括未拆分的模块——的集合，称为 hierarchy
设计时一般两头并进

EXP 9-input parity generator

Top Level: 9 inputs, one output
2nd Level: Four integrated 3-input odd function blocks
3rd Level: 3-input odd function circuit as interconnected exclusive OR blocks
Primitives: exclusive-OR block as 4 interconnected four NAND gates
Design requires 4 X 2 X 4 = 32 2-input NAND gates

集成电路(integrated circuits) 又叫 芯片(chip)，分为如下若干等级：

SSI(small-scale integrated) 内含不到 10 个 gates；
MSI(medium-scale integrated) 内含 10 ~ 100 个 gates；
LSI(large-scale integrated) 内含成百上千个 gates；
VLSI(very large-scale integrated) 内含成千上亿个 gates；

技术参数

门的实现主要通过这些参数特性来描述：

Name	Description
Fan-in	一个门可用的输入
Fan-out	一个栅极输出驱动的标准负载数量
Logic Levels	被认为是高低电平的输入输出电压范围
Noise Margin	对外界噪声的容忍能力(具体来说是不会导致行为异变的最大噪声压值)
Cost for a gate	继承电路的门成本
Propagation Delay	信号改变后从输入到输出所需的变化时间
Power Dissipation	电源输出能耗和门的能耗

扇入扇出

扇入描述了一个门能够接受的最多输入量
- 如一个四输入与非门的扇入就是 4
扇出描述的则是一个门的输出(栅极输出)在不降低工作性能的情况下能够负载多少门
- 例如一个非门的输出能够同时负载 4 个非门并且都能正常工作，则其扇出为 4

标准负载：所谓的标准负载，是衡量“负载”的一个“单位砝码”。其大小等于一个非门(逆变器)贡献的负载压力。

为描述负载，引入过渡时间的概念

延迟以及相关问题

过渡时间(transition time)

转换时间

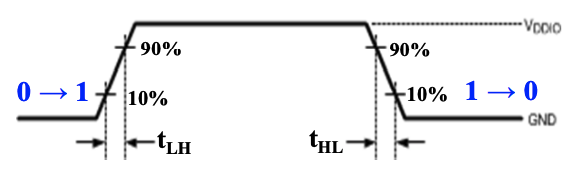
转换时间分为$ t_{LH}(rise time) $和 $t_{HL}(fall time)$ 两个部分。

rise time 等于栅极输出从 $V_{CC} $ 的 10% 升高到 90% 所需要的时间；
fall time 等于栅极输出从 $V_{CC} $ 的 90% 降低到 10% 所需要的时间；

通过时序图表示就是这样：

传播延迟(propagation delay)

传播延迟(propagation delay) 衡量了门的输入变化导致输出变化所需要的时间。

由于从低电平转化到高电平和高电平转化到低电平所需要的时间不一样，所以传播延迟同样有两个部分，分别使用$ t_{PHL}$ 和 $t_{PLH}$ 来表示。

更具体的来说，传播延迟的计算方法是输入和输出的变化中点的时间差，通过时序图表示就是这样：

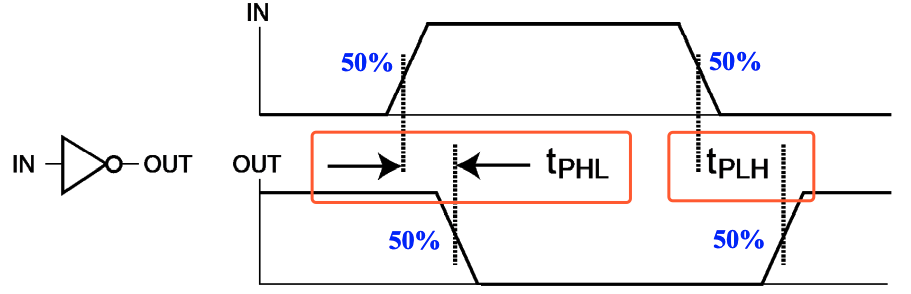
我们还可以引入 $t_{pd}$ 来统一表示 $ t_{PHL}$和 $t_{PLH}$ 。其有两者规则：

$t_{pd}=average( t_{PHL}+t_{PLH})$

$t_{pd}=max( t_{PHL}+t_{PLH})$

Transition Time vs. Propagation Delay

转换时间专注于输出的变化，而传播延迟则包含了输入的变化和输出的变化整个过程。

从时序图上的表示来看，转换时间只需要输出的时序图即可表示；但传播延迟则是通过比较输入和输出的偏差来表示的。

符号H、L的顺序两者是反过来的

延迟模型

由于存在延迟，许多在数学意义上没有问题的逻辑表达式在电路中就存在非常大的问题。

为了研究为什么会存在门延迟，刻画门的 固有门延迟(inherent gate delay)，我们需要对其建模，常见的 延迟模型(delay model) 有以下两种：

传输延迟(transport delay): 认为输入和输出之间的延迟是一个定值的

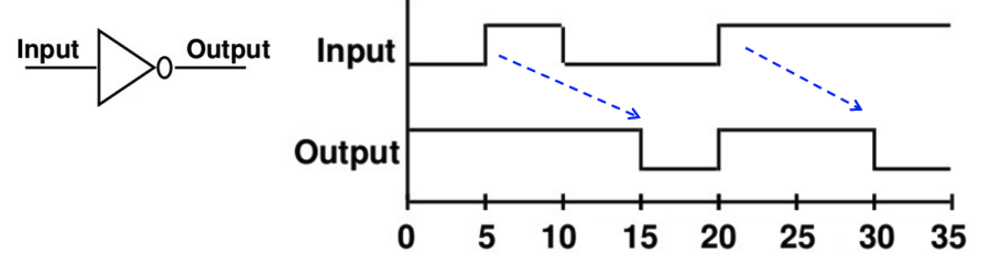
惯性延迟(inertial delay): 引入了 拒绝时间(rejection time)，只有当输入达到一定能量后，才会触发栅极输出。小于临界值的变化都无法触发输出
- 与传输延迟的显著区别在于，在这种模型下，噪音等会被过滤

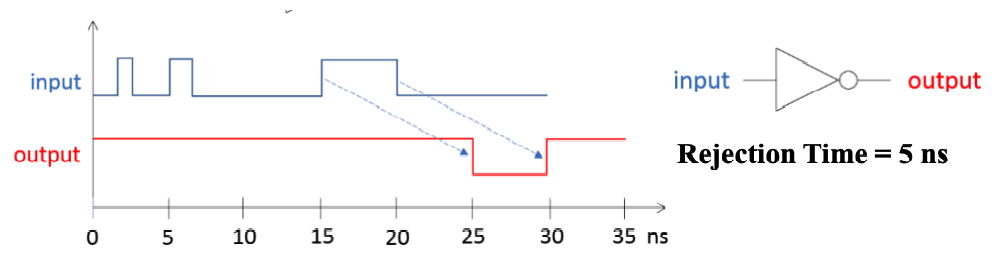
下图展示了无延迟、传输延迟、惯性延迟的时序图

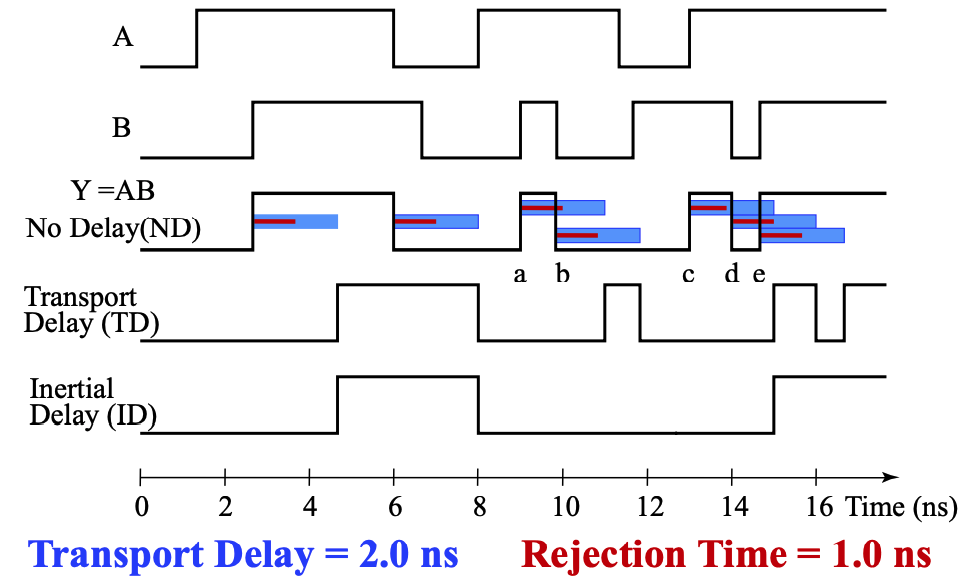
！！延迟计算

正逻辑和负逻辑

正逻辑(positive logic) 就是 1 是有效信号，负逻辑(negative logic) 就是 0 是有效信号。

正逻辑中 AND 门的作用就等效于负逻辑中 OR 门的作用，这也正体现了与和或的对称。

而正逻辑的电路的符号一般就是正常的逻辑门符号，而负逻辑的逻辑门符号则可能有小三角标，即 极性指示器(polarity indicator)：

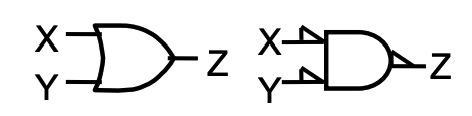
工艺映射

工艺映射(technology mapping) 是指将逻辑图或网表转化为可以用工艺实现的心的图或网表的过程。

有时我们会使用与非门/或非门和非门替换与门和或门(因为电路层面，与门实际上就是通过与非门实现的)

验证正确性

最基本的验证正确性方法有：

人工逻辑分析(Manual Logic Analysis)：
- 找到最终电路的真值表或布尔代数式，判断其是否和预期行为一致；
仿真(Simulation)：
- 在仿真环境中，使用合适的测试输入（激励信号）来测试最终电路（或其网表，可能编写为 HDL），通过观察其响应结果来判断是否实现预期行为；

Chap3 组合逻辑 coder+multiplexer

基本逻辑函数

常量函数(Value-Fixing)：$F=0$ or $F=1 $ | 输出定值；
传输函数(Transferring)：$F=X$ | 直接输出输入值；
逆变函数(Inverting)：$F=\overline{X}$ | 输出输入的相反；
使能函数(Enabling)：$F=X\cdot En $ or $F=X+\overline{En}$ | 通过使能控制输出是否可变
- 分为两种，比如与的形式中，只有 $En$为 1 时，$F$表现为 $X$ 的值；反之输出必定为 0；

基本功能块

译码器(Decoder)
编码器(Encoder)
（三端）多路复用器(Multiplexer) MUX
（三端）信号分配器(Demultiplexer) DEMUX

译码器

穷举可能性，稠密 -> 稠密/稀疏

为了节省门输入成本，我们常常使用分级的思想来构造多输入译码器

eg

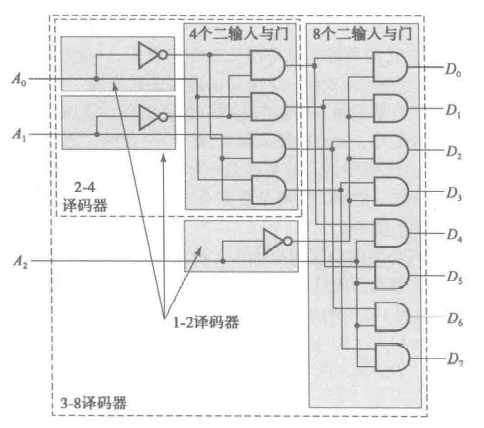
编码器

稠密/稀疏 -> 稠密

如上定义的编码器有一个限制，即任何时候输入只能有一个是活动的，即输入是 one-hot 的。即同一时刻的输入中只能有一个是1，其它都是0

优先编码器

优先编码器能够实现优先级函数，它不要求输入是 one-hot 的，而是总是关注有效输入中优先级最高的那一个。即比如当优先级最高的那一位是 1 时，其它所有优先级不如它的位置的值都是我们不关心的内容了。

多路复用器

通过控制端选择输出的是若干输入中的哪一个

三态门实现的MUX，门输入大大减少

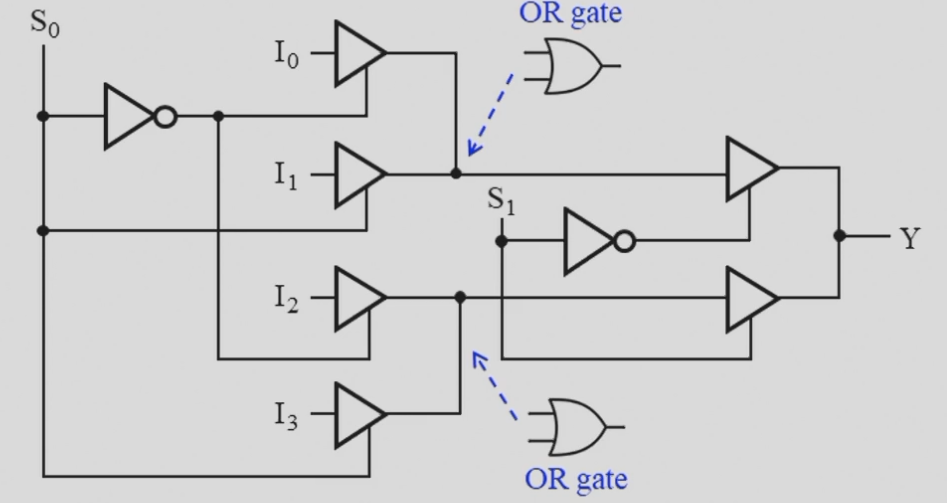
信号分配器

简写为 DEMUX，通过控制端选择输入给到若干输出中的哪一个。

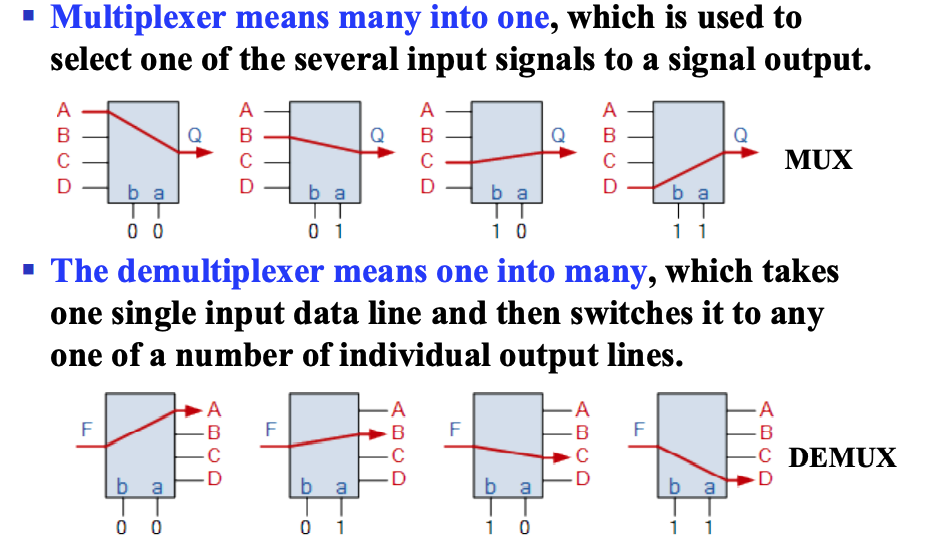
Chap3 算术逻辑电路

我们讨论的计算主要包括逻辑运算和算术运算，前者由于可以直接通过基本门很方便实现

在计算机硬件中，承担计算工作的主要部件为 ALU(Arithmetic Logical Unit)

首先我们需要了解加法器最底层的单元，即实现 1 bit 运算的 半加器(half adder) 和 全加器(full adder)接下来需要将他们组合在一起，实现 n bits 的加法器，其中主要介绍 行波加法器(binary ripple carry adder)。此外，基于一些编码的知识，我们还可以将它改装成加减法器。

半加器 & 全加器

对于二进制加法，其输出有当前位的和 S 和进位 C，而输入除了两个操作数 X 和 Y 以外，还可能有上一位的进位 Z(或者C{n-1})。

对于一个二进制数的第一位，显然不会有进位，或者说 Z=0，所以我们可以将这个 Z 去掉，即输入只有 X 和 Y，这就是 半加器(half adder)；
对应的，如果输入中有上一位的进位 Z，则称为 全加器(full adder)。

半加器

逻辑表达式 $$ S=\overline{X}Y+X\overline{Y}=X⊕Y*C=XY $$ 真值表

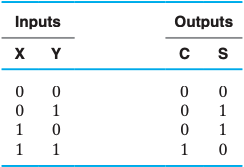
电路图

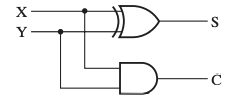
全加器

逻辑表达式 $$ S= \overline{X}

\overline{Y} Z+ \overline{X} Y \overline{Z} +X \overline{Y}

\overline{Z} +XYZ \ C=XY+XZ+YZ $$ 逻辑表达式(with XOR) $$ S=(X⊕Y)⊕Z \C=XY+Z(X⊕Y) $$

真值表

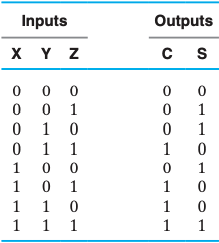
卡诺图

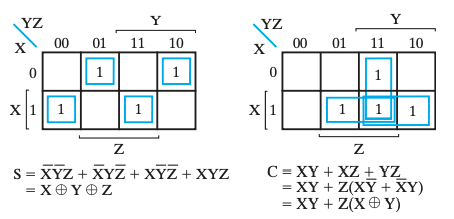
行波加法器

行波加法器是朴素的 n bits加法器实现。使用行波加法器，随着位数增加效率会越来越慢

核心思想：模拟“竖式”来计算加法，从低位开始逐位计算，并将进位给到下一位作为输入。

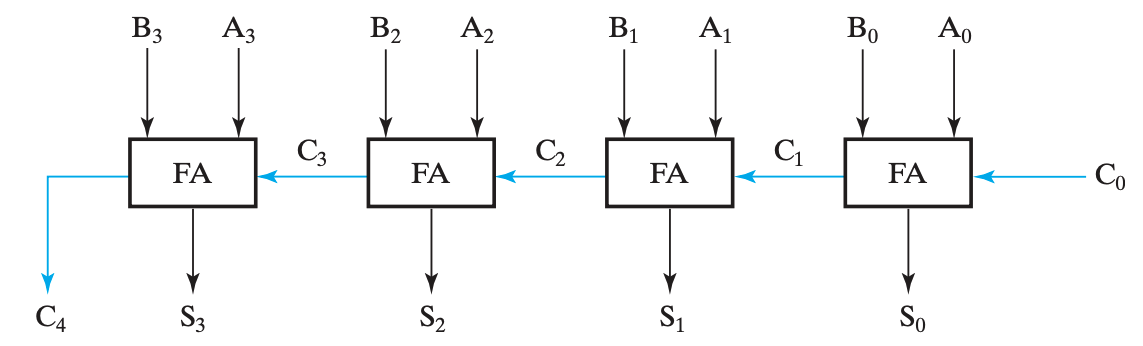
$C_0$必然为0

！！超前进位加法器

二进制减法

反码(1's complement)

计算：负数*除了符号位取反，N的反码为 $2^n-1-N$, n为digit（位数）

补码(2's complement)

为了方便计算机内的运算，一般用补码表示数值

计算：负数除了符号位取反加一，即$2^n-N$

技巧，从右到左第一个1以及其右边的0都不变，左边的全取反，即得补码

无符号减法

！！有符号数的表示与计算

有符号减法

有符号数：第大位为0时表示正数，为1时表示负数

有符号数的反码、补码：符号位不能动，对剩下的位数操作

算法：

Overflow(溢出)

即两个n位数算完结果成n+1位了

加减法器

结合补码，我们再来观察行波加法器，我们需要对减数的每一位取反，并对整个数加一，再直接将它们相加即可，即将减法转化为补码下的加法。

其中加一这一步恰好可以通过在加法器中必定为 0 的 $C_0$来实现。

我们在输入中添加异或门来实现反码(1's complement)，再用 $C_0$ 实现加一，从而得到补码(2's complement)，就样就可以实现加减法器。

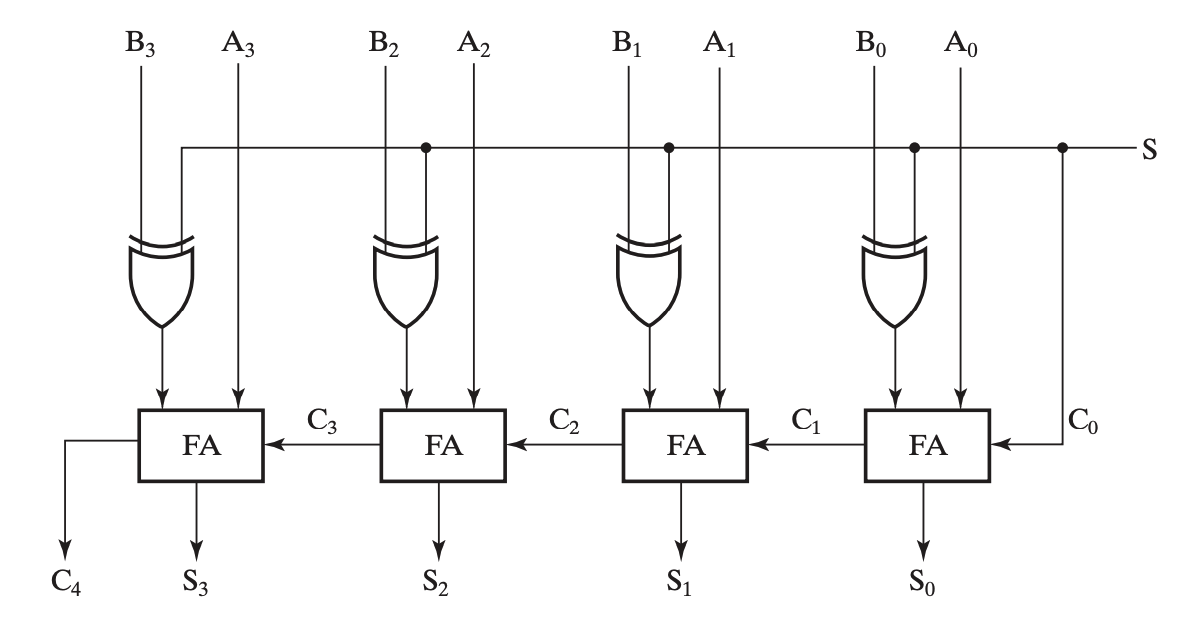
Design by Contraction（压缩式设计）

即对于某复杂电路，在输入固定不变的特殊情况下，可化简电路，保证输出相同即可

lncrementing & Decrementing

前者为将输入加上某固定数的操作，后者为减。相应的电路模块叫lncrementer & Decrementer

乘除法($2^n$)

当乘除2的倍数时，只需移位即可

MSB&LSB

即最高位和最低位

Chap-4 Sequential Circuits

组合电路存在一些的问题：

对于复杂的逻辑，抽象层级多，导致硬件层面开销大、耗时长，一方面提高成本，一方面降低效率；

组合电路没法实现信息的存储，所有的功能模块对于特定的输入给出相同的输出；

时序电路则拥有存储信息的能力，对于时序电路来说，输出除了与输入有关（甚至可以没有输入），也可以与自身 状态(state) 有关。

时序电路主要分为两类：

同步时序电路(synchronous sequential circuit)
异步时序电路(asynchronous sequential circuit)。

The behavior of a synchronous sequential circuit can be defined from the knowledge of its signals at discrete instants of time.

The behavior of an asynchronous sequential circuit depends upon the inputs at any instant of time and the order in continuous time in which the inputs change.

一般来说，异步电路的设计相对困难（行为与门的传播延迟和输入信号变化的时间序列密切相关），但仍然十分必要，比如触发器就是以异步锁存器为模块设计的。

同步电路的使用更加广泛，通常这些“离散的时刻”都是由 时钟发生器(clock generator) 这种时序器件产生周期性的 时钟脉冲(clock pulse) 序列来实现的

这种电路一般被称为 钟控时序电路(clocked sequential circuit)，由于设计相对容易，鲁棒性强，所以被广泛应用

缓冲

缓冲器(buffer) 一般通过两个非门串联，并将输入连通输出实现，这样能够实现信息的存储，然而无法修改。

其中，从给定输入到更新输出有一个 $t_G$ 的延时。

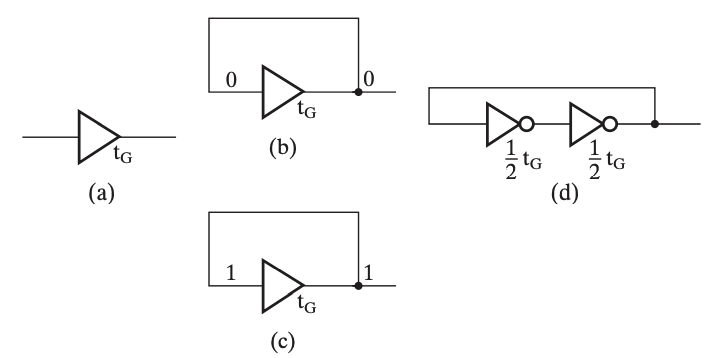
而锁存器就是在缓冲器的基础上，将非门替换为或非门或与非门实现的。

显然，时序电路中最重要的就是信息存储元件。

当输入信号不发生变化时（重点是变化，即输入和存储信息未必存在对应关系）存储元件就能够保持其内部存储的二进制数据。

存储元件主要由 锁存器(latch) 和 触发器(flip-flop) 两种，其中前者是后者的基础，或者说多数情况下我们使用后者，但后者由前者构成。

锁存器

SR & S'R' 锁存器(Latch)

SR 锁存器和 S'R' 锁存器的输入都是 S(Set) 和 R(Reset) 两个部分，输出都是 Q 和 Q' 两个部分。

SR 锁存器和 S'R' 锁存器的基本原理是一致的，只不过前者用的是或非门，后者用的是与非门。

SR锁存器

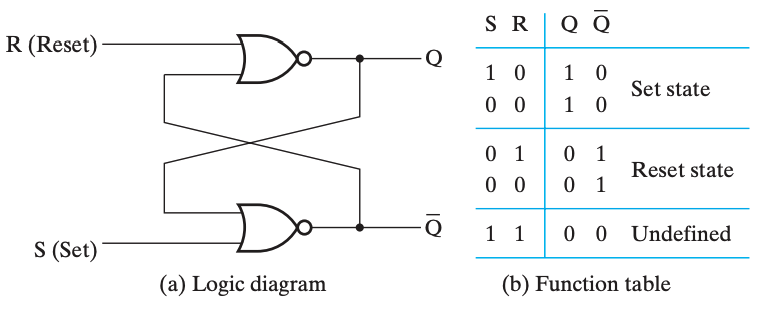
S'R' 锁存器

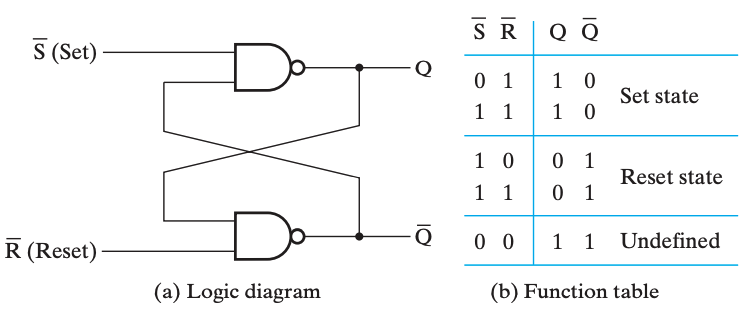
一个记忆方法是，SR 的门元件对 1 敏感，所以是或非门的实现；而 S'R' 的门元件对 0 敏感，所以是与非门的实现。而通过「当 S 为 1 时，Q 都会是 1」可以得到 S、R 与 Q、Q' 的位置。

由于电路存在延时，所以 S 和 R 的输入很难同时到达，所以我们可以在前面加一个控制端，当确保两个输入都到位的时候再使能。

带控制输入的 SR 锁存器(SR Latch with Control Input)

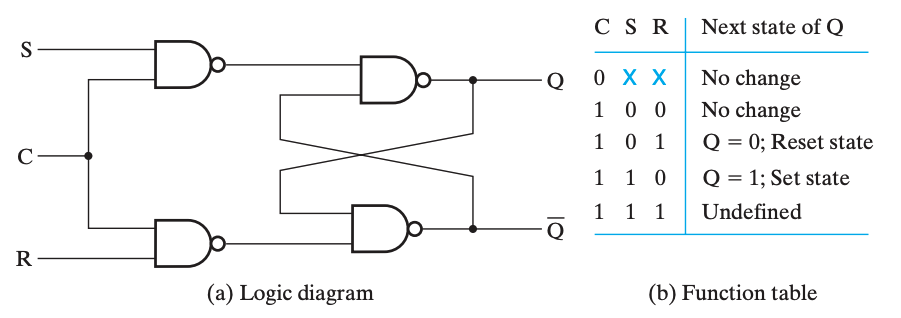
D 锁存器

D 锁存器实际上是带控制输入的 SR 锁存器的改进。

即使是带控制输入的 SR 锁存器，也存在一个「undefined」状态，而这是我们不希望出现的。由于可以通过 C 来控制是否保持，所以可以直接强制要求 $S=\overline R$，于是就避免了 undefined 情况的出现，这就是 D 锁存器(D Latch)。

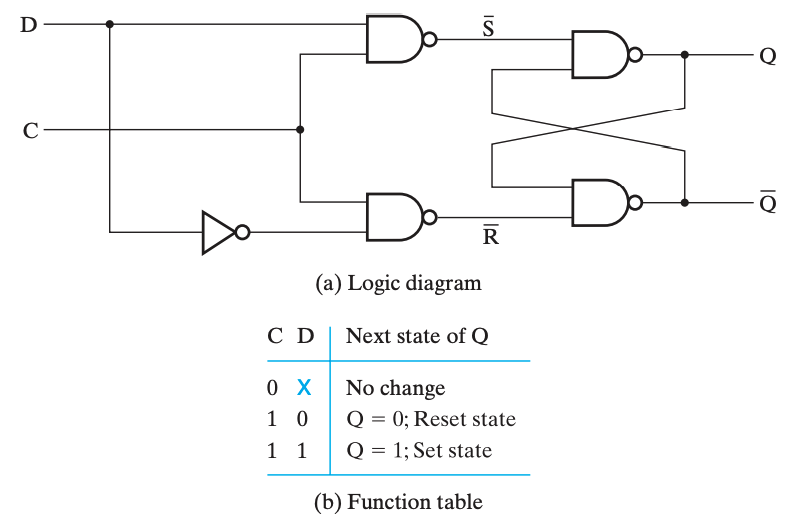
只有当 C 为 1 时，D 锁存器才能写入数据；而当 C 为 0 时，D 锁存器的数据就不会变化。

☠ 透明的危害：空翻

如果将 $\overline Q$ 接到 $D$ 上，就会发现 $C$ 置 1 时 D 锁存器将不停的变化其中的数据，出现空翻，导致我们无法确定 C 置 0 时 Q 的输出究竟是什么，而这是非常危险的。

这主要是因为 D 锁存器的输入和输出都是直接暴露出来的、同时允许变化的（不是同时变化，是指在 Input 可以变的时候 Output 也能变），即 透明(transparent) 的。这就导致了在一个时钟周期里，同时存在 可以互相影响 的两个东西。这也是触发器所解决的问题。

触发器(flip-flop)

为了解决上面提到的，由「透明」引发的问题，而采用触发器的设计。通过组合两个锁存器，主要有两种实现方法：

主从式(master-slave)触发器：在有脉冲（高电平）时，修改第一个锁存器的值，保持第二个锁存器的值；在没有脉冲（低电平）时候保持第一个锁存器的值，修改第二个锁存器的值，更新触发器的状态；
边沿触发式(edge-triggered)触发器：仅在时钟的边缘触发，即在特定时刻仅接受一个输入；

边沿触发式 D 触发器是目前使用最广泛的触发器。

SR 主从触发器

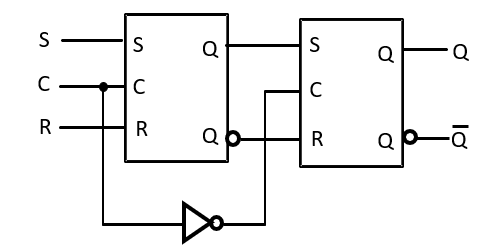
边沿触发式触发器

下图为上升沿触发(positive-edge-triggered)的 D 触发器的大致原理图（将 C 前的非门去掉则可得到下降沿触发(negative-edge-triggered)的 D 触发器）。

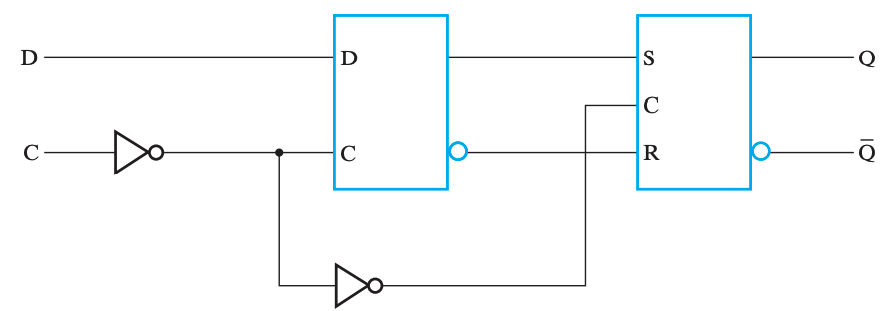
作为主锁存器，右为锁存器

标准图形符号

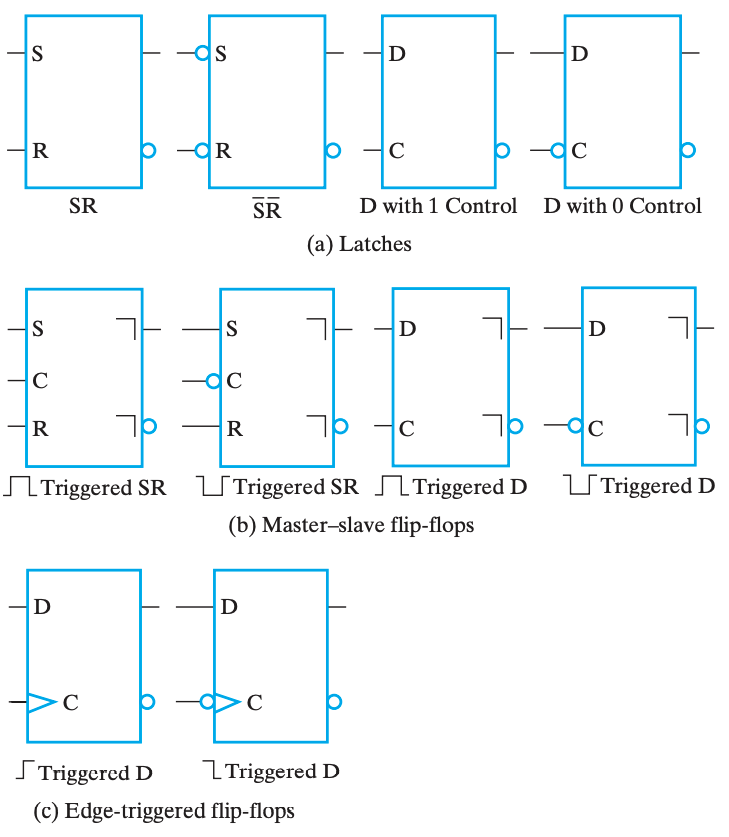
触发器的基本描述方法

理论分析中：
- 状态表(Characteristic Table, or State Table)用输入和当前状态来描述下一状态；
工程设计中：
- 激励表(Excitation Table)用当前状态和下一状态来描述输入（展示从当前状态转移到下一状态所需要的输入）；

时序电路分析

为了分析时序电路，我们需要一些工具来表示时序电路的一些特征与逻辑。观察时序电路和组合电路的区别，发现最核心的就是逻辑运算过程中出现了「状态」参与运算。因此，我们需要在各个组合电路分析中采用的表示方法中，添加表示「状态」的信息。

触发器的输入方程

触发器的输入方程(flip-flop input equation) 主要是为其提供一个代数表达方式。它的主要想法是：

⓵表达每一个触发器的输入与输出之间的关系；

⓶表达每一个直接输出的逻辑表达式。其中，触发器的输出符号表示了其类型（即符号）与输出（即下标）。

具体来说，例如下面这个电路：

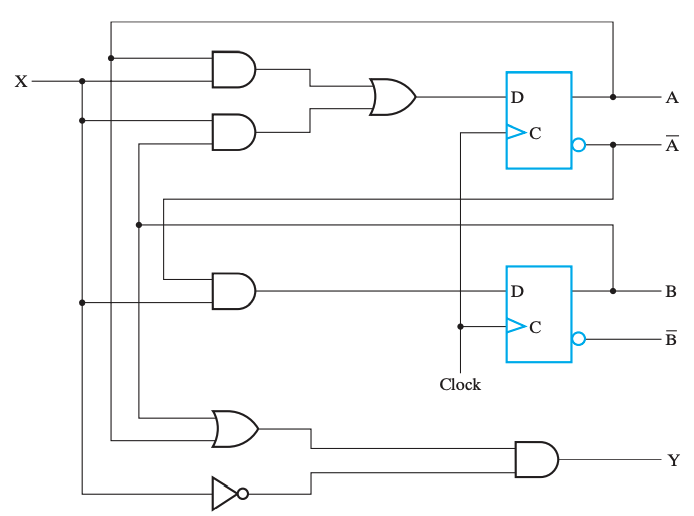
可以发现，其中包含两个触发器 $D_A$ 和 $D_B$，以及一个组合逻辑输出 Y，因而可以根据电路的特征，得到下面这几个式子： $$ D_A=AX+BX\D_B=\overline AX\Y=(A+B)\overline X $$

状态表

时序电路的逻辑有时候可以通过状态表来描述，只不过与组合电路的真值表不同，状态表(state table) 有四栏：

当前状态(present state)
输入(input)
下一状态(next state)
输出(output)

其含义是比较显然的，只不过通过电路图得到状态表，需要首先得到「当前状态」向「下一状态」转移的方程，即对于某个时刻 t 的触发器 A 的输出 A(t ) ，需要得到它下一刻的状态 A(t+1)=f(A(t), …)。

eg

依旧用上面那个图

首先我们对 $D_A$ 得到转移方程：$A(t+1)=D_A=A(t)X+B(t)X$，可以简写为 $A(t+1)=D_A=AX+BX$。类似地也能得到 B 的转移方程。

于是，根据这些信息，我们可以写出它的状态表：

Present State `AB`	Input `X`	Next State `AB`	Output `Y`
`00`	`0`	`00`	`0`
`00`	`1`	`01`	`0`
`01`	`0`	`00`	`1`
`01`	`1`	`11`	`0`
`10`	`0`	`00`	`1`
`10`	`1`	`10`	`0`
`11`	`0`	`00`	`1`
`11`	`1`	`10`	`0`

状态图

状态表比较清晰的表达了不同的状态和输入得到的结果，但是对于「不同状态之间是如何转换的」这件事的描述并不清晰。而对于「联系」这件事，有向图是一个非常好的形式，所以我们将介绍 状态图(state diagram)。

状态图承载的信息量和状态表是一样的，所以也是需要表达当前状态(present state)、输入(input)、下一状态(next state)、输出(output) 这四个东西。只不过「下一状态」是通过有向边来表示的。

当前状态作为一个 node 的属性；而输入作为 edge 的一个属性；至于输出，根据它是放在 edge 上还是 node 上，分为 米勒型(Mealy) 和 摩尔型(Moore) 两种。

Mealy

这是一个米勒型的状态图，以及对应的状态表。

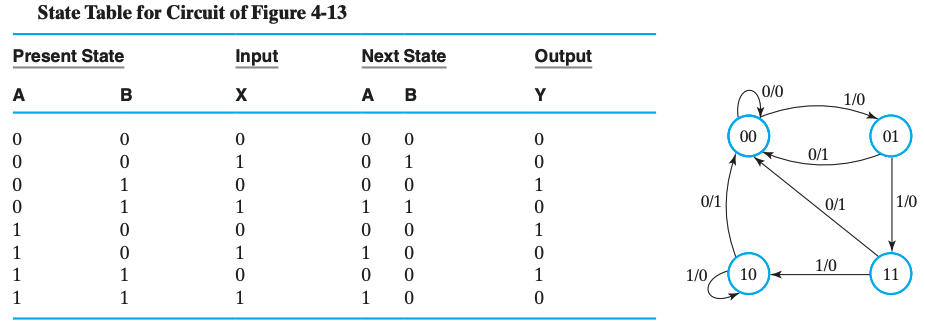
因为米勒型电路的 输出与当前状态和输入都有关，所以输出会和输入放在一起，即放在 edge 里。

node 内的二进制为 present state 中的 AB；

edge 上分别为 input 和 output：X/Y；

有向边表达了每个状态在特定输入下的下一个状态。

例如，关注 node 00，它有一条自环 0/0，对应状态表的第一行；它有一条 edge 1/0 指向 node 01，对应状态表的第二行。

当然，米勒型是有缺陷的，在时序电路设计之后的步骤中，我们需要根据它来对每一个状态设计输出方程。此时由于两个输出共享同一个目标状态，所以我们需要将两个输出结合到同一个式子中，这将提高设计难度和组合电路成本。

Moore

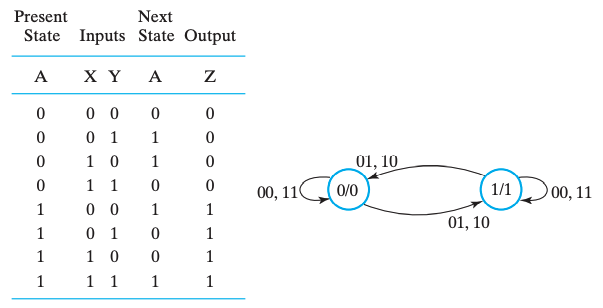
因为摩尔型电路的 输出只与当前状态有关，所以输出会和当前状态放在一起，即放在 node 里。

node 内的二进制表示 present state 和 output：A/Z；

edge 上列举了这种转移可能的 inputs：XY。

例如，关注 node 0/0，它有两条自环 00 和 11，分别对应状态表的第一行和第四行；它有两条 edge 01 和 10 指向 node 1/1，对应状态表的第二行和第三行。

摩尔型也存在缺陷的，非常显然，相比于米勒型，摩尔型需要更多的状态。

Mealy model circuit & Moore model circuit

如果输出既依赖于当前状态，也依赖于输入的时序电路，则称为 米勒型电路(Mealy model circuit)；而如果输出只依赖于当前状态，则称为 摩尔型电路(Moore model circuit)。

米勒型倾向于表达「在特定状态下，特定输入将导致某种结果，以及状态转移」；而摩尔型倾向于表达「特定输入将导致某个状态向另外一个状态转移，而输出更像是一种状态的结果」。

现实的工程设计中，有时会结合使用米勒型和摩尔型，即在同一状态图中可能混用两种类型。

等价状态(Equivalent State)

对于两个状态，如果它们对于同一输入序列的响应是完全相同的（包括相同的输出和相同的状态转移），那么这两个状态是等价的。基于此我们可以对状态图进行简化

未简化的

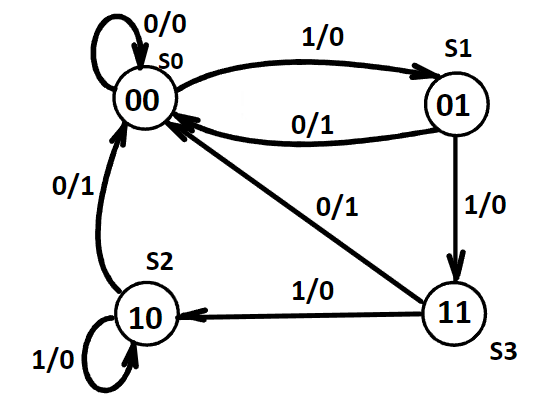
我们首先注意到，状态 S2 和 S3 对于输入 0，相应的输出都是 1，下一状态都是 S0；对于输入 1，相应的输出都是 0，下一状态都是 S2。所以 S2 和 S3 是等价状态。我们可以把这两个等价状态简化成同一个状态，记为 S2。

更进一步地，我们注意到 S1 和新的 S2 也是等价状态，我们继续化简它们。

寻找等价状态并合并它们，不断重复这个过程就可以实现状态图的简化。

简化后的

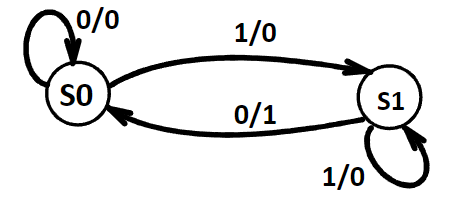
状态机(Generic State Diagram Template)

Chap 4 Sequential Circuits - Isshiki修's Notebook (isshikih.top)

时序电路的设计

类比组合逻辑电路通过真值表设计电路，（同步）时序电路主要依据状态表（或等价表达，如状态图）来设计电路。

实际设计中，我们需要考虑触发器以及其它组合电路的选择与设计：

触发器的数量基本取决于整个需求中状态的数量，n 个触发器能够表达$ 2^{n}$ 个二进制状态；
组合电路的主要设计围绕触发器的输入和输出展开；

而主要的设计过程和组合逻辑电路的设计是类似的，如下：

确定系统的行为；
1. 描述系统行为过程中，要注意状态的复用（不过并非状态越少成本就越小，这里有触发器数量和组合逻辑电路的 trade-off）；
2. 确定电路的初始状态（复位状态(reset state)，通过给定复位(reset)信号实现）； - 复位一般可以是异步的；
阐述输入和输出之间的逻辑关系，并用真值表或逻辑表达式表达出来；
给设计好的状态编码赋值，得到具体的状态表；
1. 我们可以使用按计数顺序、按格雷码、用独热码来给状态赋值，更系统的方法比较复杂，不做讨论；
2. 其中还有一种情况是所需要的状态不能完整填充 $2^n$ 种情况，需要设计无效状态，这种时候可以不考虑它们；
根据状态表确定使用的触发器及其输入方程；
根据状态表确定输出方程；
优化输入方程和输出方程；
将优化后的逻辑设计工艺映射到硬件实现上；
验证正确性（在仿真环境中）；
- 主要就是看能不能复现状态图；

延时分析

首先，自上而下的给出观念，时序电路的延时分析有两个主要部分和一个次要部分：

组合电路导致的延时；
触发器导致的延时；
电路的松弛时间；

并且往往是根据触发器的类型，计算一个时钟周期的时间。

最核心的问题就是计算电路能够正常工作的最短时钟周期。接下来，自上而下地进行细节补充。

触发器延时

触发器延时相比组合电路延时复杂很多，主要目的是为了保证采样。也就是说它的“延时”并不仅仅是因为电信号传播的延迟，还有为了保证信号稳定设计的一些内容。

大致来说有三个部分：

Setup Time：采样边缘前输入信号需要保持稳定的时间；
Hold Time：采样边缘后输入信号需要保持稳定的时间；
Propagation Time：触发器的采样边缘到输出稳定的时间（传播时间）；

一篇介绍 Setup Time 和 Hold Time 的文章。

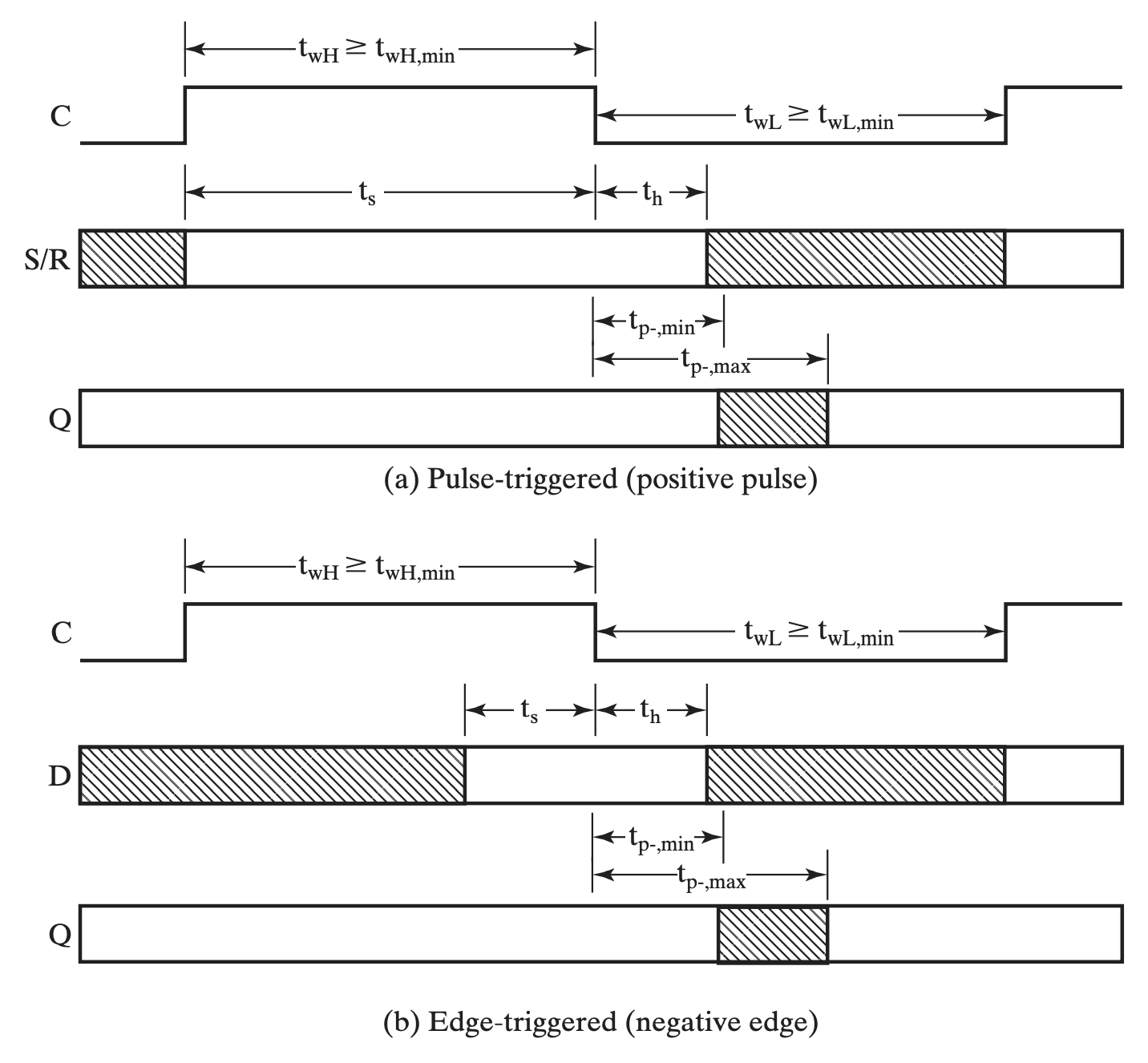
其中比较重要的一些点是：

这几个时间点起点/终点都是触发边缘；
Propagation Time 一定长于 Hold Time，因此在计算电路延迟时只考虑 Propagation Time；
Pulse-trigger 和 Edge-trigger 在表现上的区别在于 Setup Time，前者需要覆盖整个 pulse(pos or neg)；

松弛时间

实际上这就是给整个电路的一个“容差”时间，给定一个误差，但是由于通过前两者计算出来的是最短时间，所以松弛时间必定非负。（不能倒扣！）

时序电路延时

时序电路的延时计算实际上是为了计算时序电路运作的最大频率以设计时钟频率。所以我们需要算出电路能够稳定工作的最小时钟期。

其计算遵循一定方法：

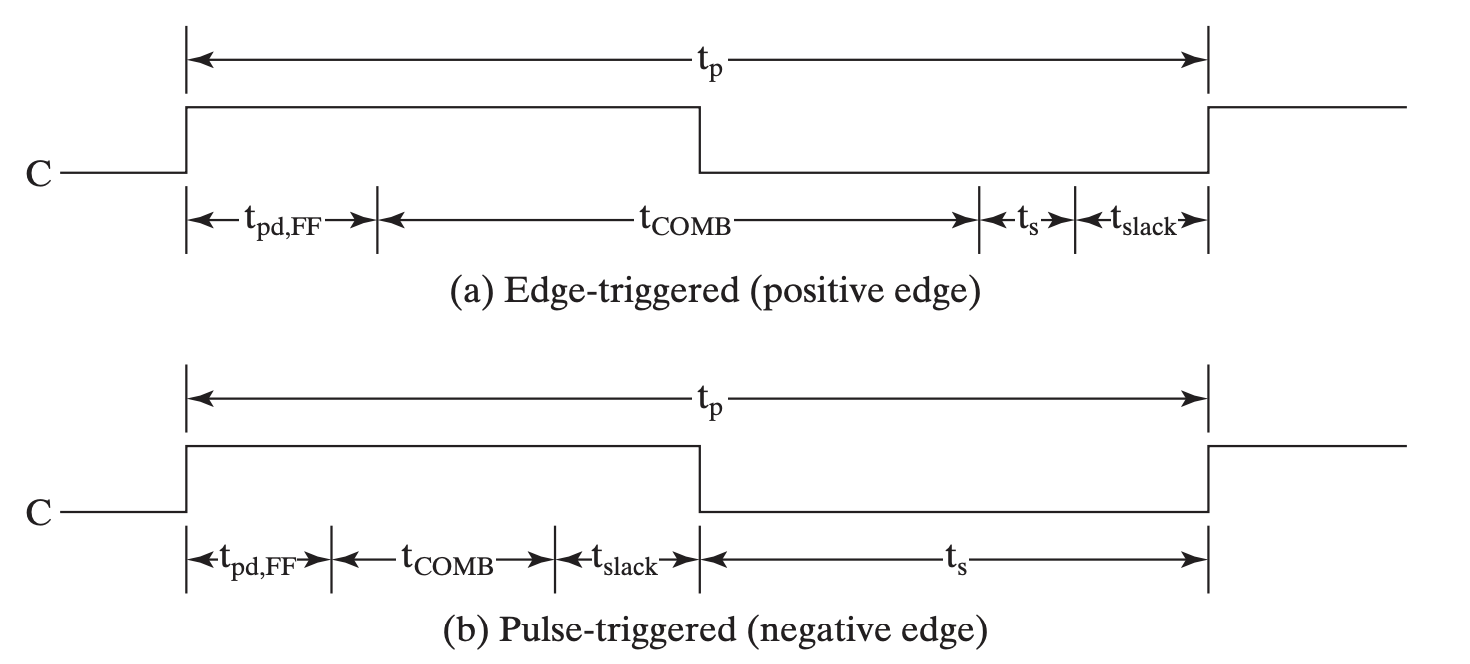
（假）经验之谈

一般从一个 FF 的输出出发到 FF 的输入结束。

eg

Chap5 Digital Hardware Implementation

⛵引入

本章内容主要关于数字逻辑的硬件实现，分别介绍 设计空间(The Design Space) 和 可编程技术(Programmable Implementation Technologies)：

在数字逻辑的设计空间中，COMS 凭借其较高的抗噪性能和较低的能耗，成为目前应用最广泛的硬件技术之一；

可编程技术使得硬件在出厂后，能够根据用户的需求进一步编辑硬件，从而实现特定的逻辑功能；

更进一步地，可编程技术又可以分为永久(permanent)编程技术和可重(reprogrammable)编程技术；

设计空间

集成电路¶

集成电路(IC)这部分内容在 第三章#集成电路 中已经介绍过了，此处不再赘述。

CMOS

✒前置知识

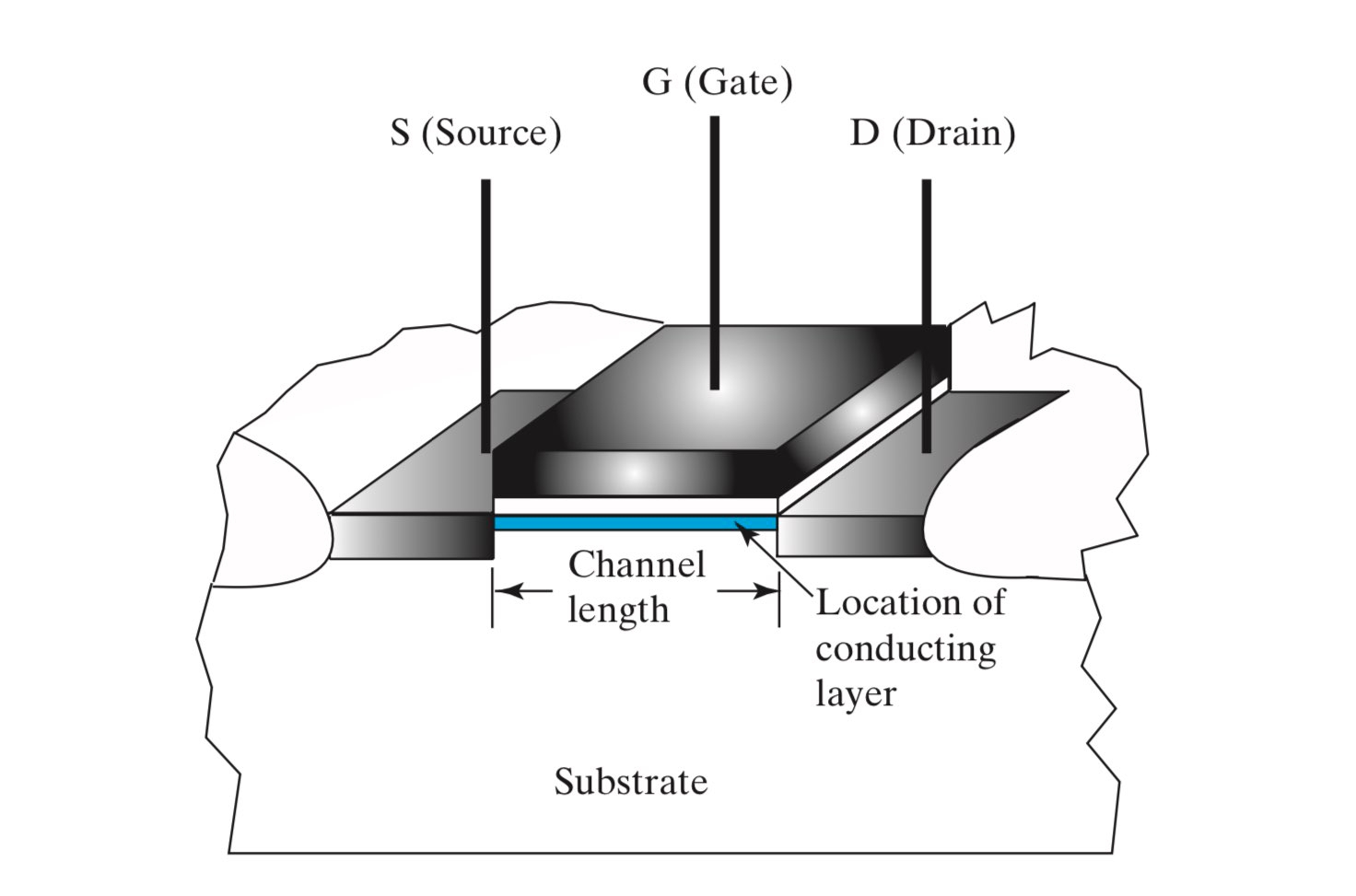
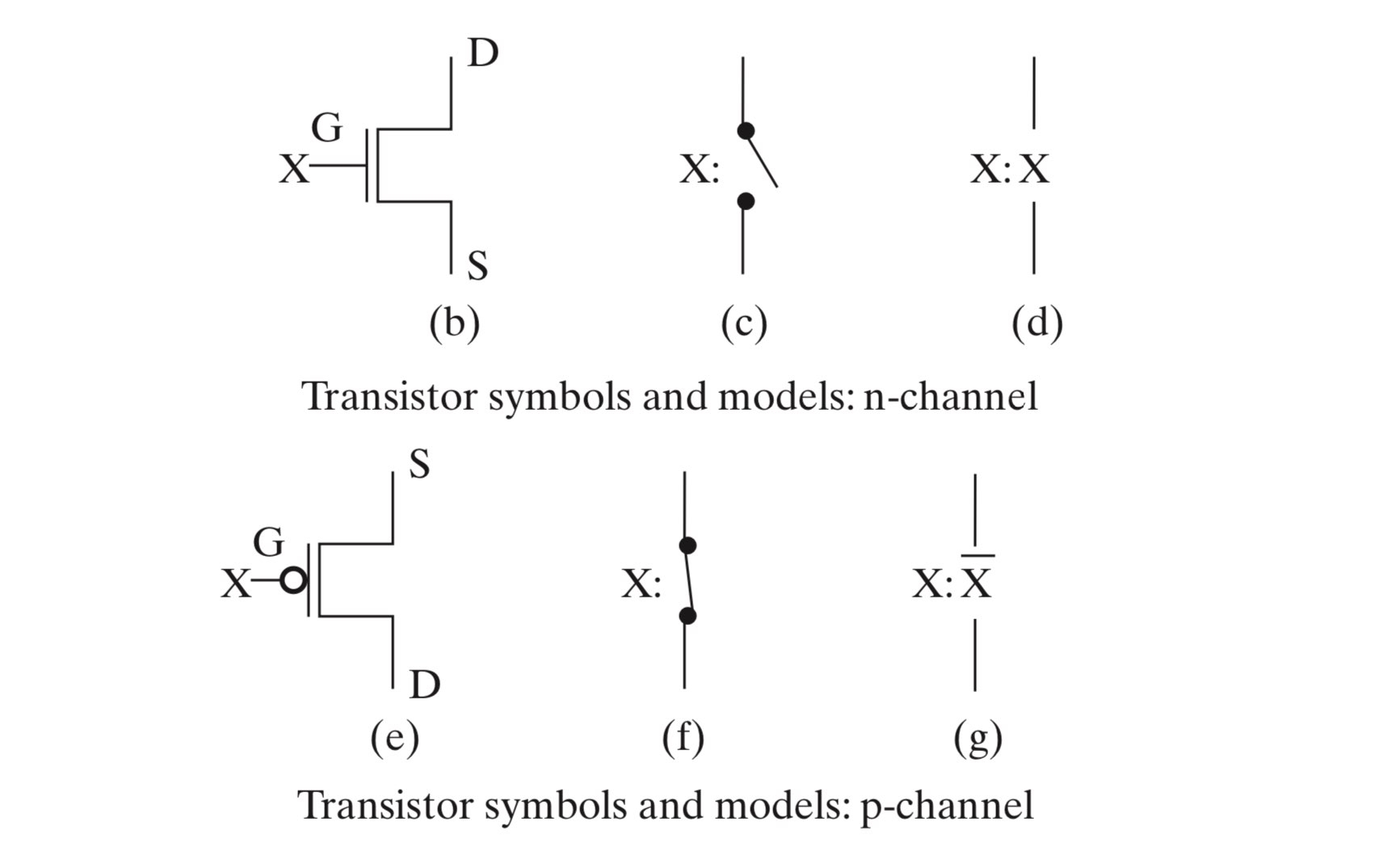
金属氧化物半导体场效应管(Metal-Oxide-Semiconductor Field-Effect Transistor， or MOSFET)简称 MOS，是一种广泛应用于数字电路和模拟电路的硬件。MOS 的基本结构如下图所示，其具体工作原理此处不做展开，我们只需要知道，MOS 的作用相当于一个开关，通过控制门极(Gate)的电压，来控制 MOS 的开闭。

互补式金属氧化物半导体(Complementary Metal–Oxide–Semiconductor)简称 CMOS，是集成电路中最重要的一种设计工艺。其主要有对称的两部分组成，这两部分分别使用了 n-channel MOS(NMOS)和 p-channel MOS(PMOS)。

对于 NMOS，门极输入 X 为 0 时断开（称为“常开”），X 为 1 时导通；对于 PMOS，门极输入 X 为 0 时导通（称为“常闭”），X 为 1 时断开。

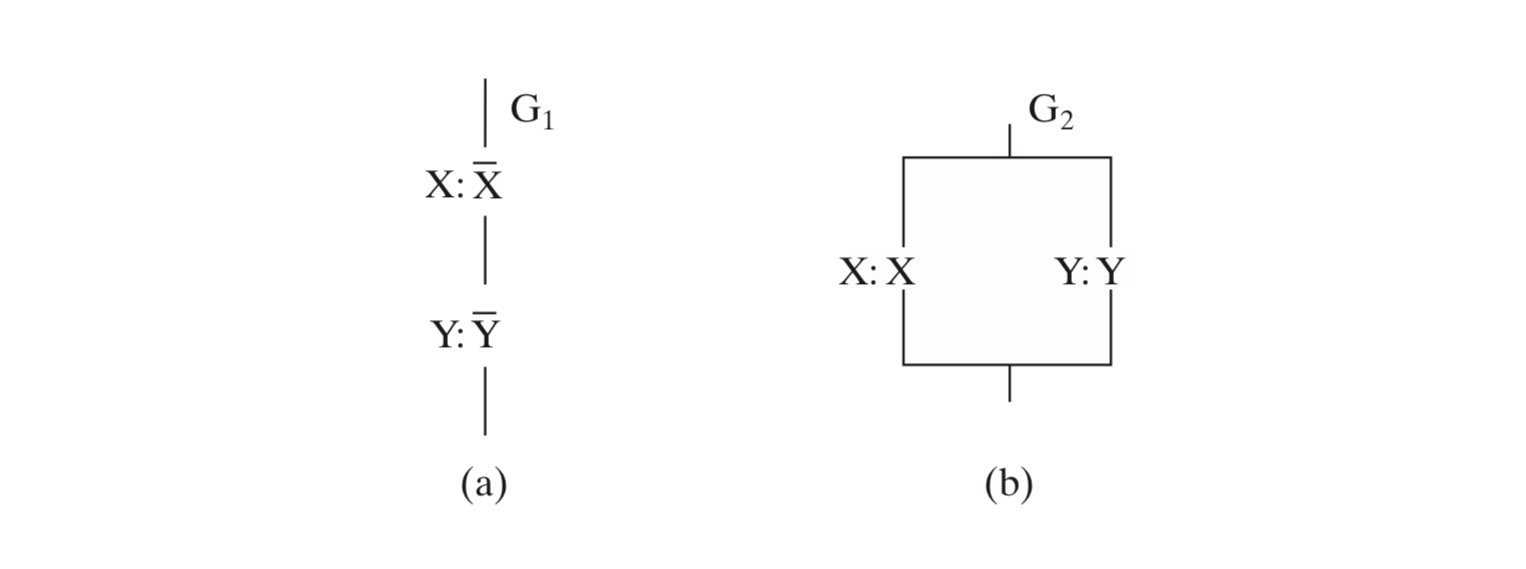
更进一步地，我们可以利用 MOS 的开关特性，来实现一些简单的“与”和“或”的逻辑（注意这里的实现是有问题的，真正的实现应该用 CMOS）：

左图实现了 $\overline X \cdot \overline Y$，右图实现了 X+Y。

Chap 5 Digital Hardware Implementation - Isshiki修's Notebook (isshikih.top)

可编程技术

直接更改硬件布线来修改电路功能被称为硬编程

可编程技术让我们能够在不直接更改硬件布线的情况下，利用软件编程来间接更改硬件布线。

硬编程的操作者是设计制造者(manufacturer)，而软编程的操作者是用户(user)。

可编程技术在硬件层面主要有三种实现手段：

控制连接(Control Connections)：
- Mask programing
- Fuse（类似于保险丝，通过高电压来切断部分电路来实现）
- Anti-fuse（Fuse 的反操作，通过高电压来联通部分电路来实现）
- Single-bit storage element
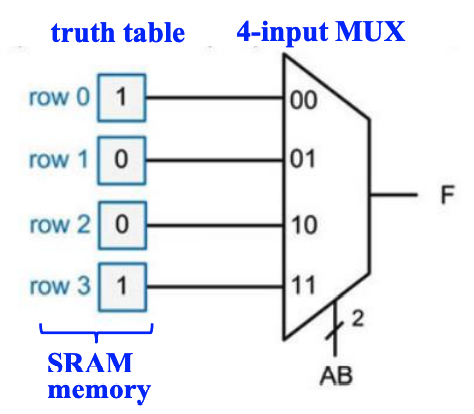
查找表(Lookup Tables)：
- Storage elements for the function
  - 比如使用一个 MUX，并将输入端接内存，通过修改内存的值来修改 MUX 的行为，进而实现函数重编程
控制晶体管开关(Control Transistor Switching)

进一步地，可编程技术可以分为 永久编程技术 和 可重编程技术 ：

永久(permanent)编程技术：出厂后经过一次编程，便永久成型；
- Mask programming
- Fuse
- Anti-fuse
可重(reprogrammable)编程技术：允许重复进行编程；
- Volatile：断电后编程信息会丢失；
  - Single-bit storage element
- Non-Volatile：编程信息仅在擦除操作后才会消失，不受断电影响；
  - Flash (as in Flash Memory)

常见的可编程技术

课程中介绍的可编程技术主要有如下四种：

只读内存 Read Only Memory (ROM)
可编程阵列逻辑 Programmable Array Logic (PAL$^Ⓡ$)
可编程逻辑阵列 Programmable Logic Array (PLA)
Complex Programmable Logic Device (CPLD)
- or Field-Programmable Gate Array(FPGA)

前三者都只能编程一次（属于永久编程技术），如下是它们的可编程内容：

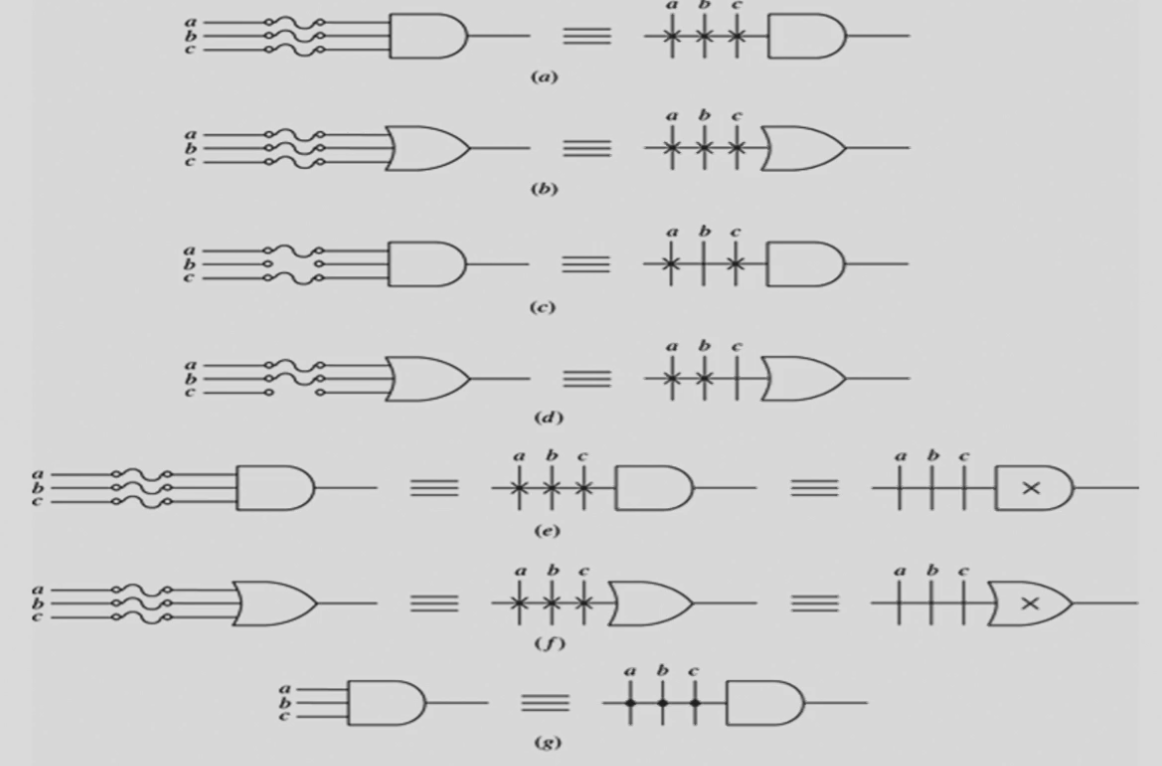
⛵由于之后出现的电路图会非常庞大，所以需要引入一些逻辑符号。

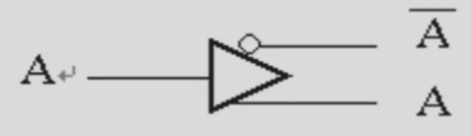
Buffer

简化表示一个变量的自身和其非；

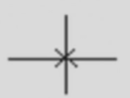
Wire connecting

在可编程逻辑电路中，线的连接不再只有单纯的连通和不连通的关系：

对于两条相交导线：

如果没有特殊符号，则表示这个交叉点 is not connected ；

如果有一个 ❌，则表示这个交叉点 is connected and programmable；

如果只有一个加粗的点，则表示这个交叉点 is connected but not programmable；

特别的，如果一个元器件的所有输入都是 programmable，我们也可以选择把这个 ❌ 画到逻辑门上（如下图 e 和 f）。

ROM

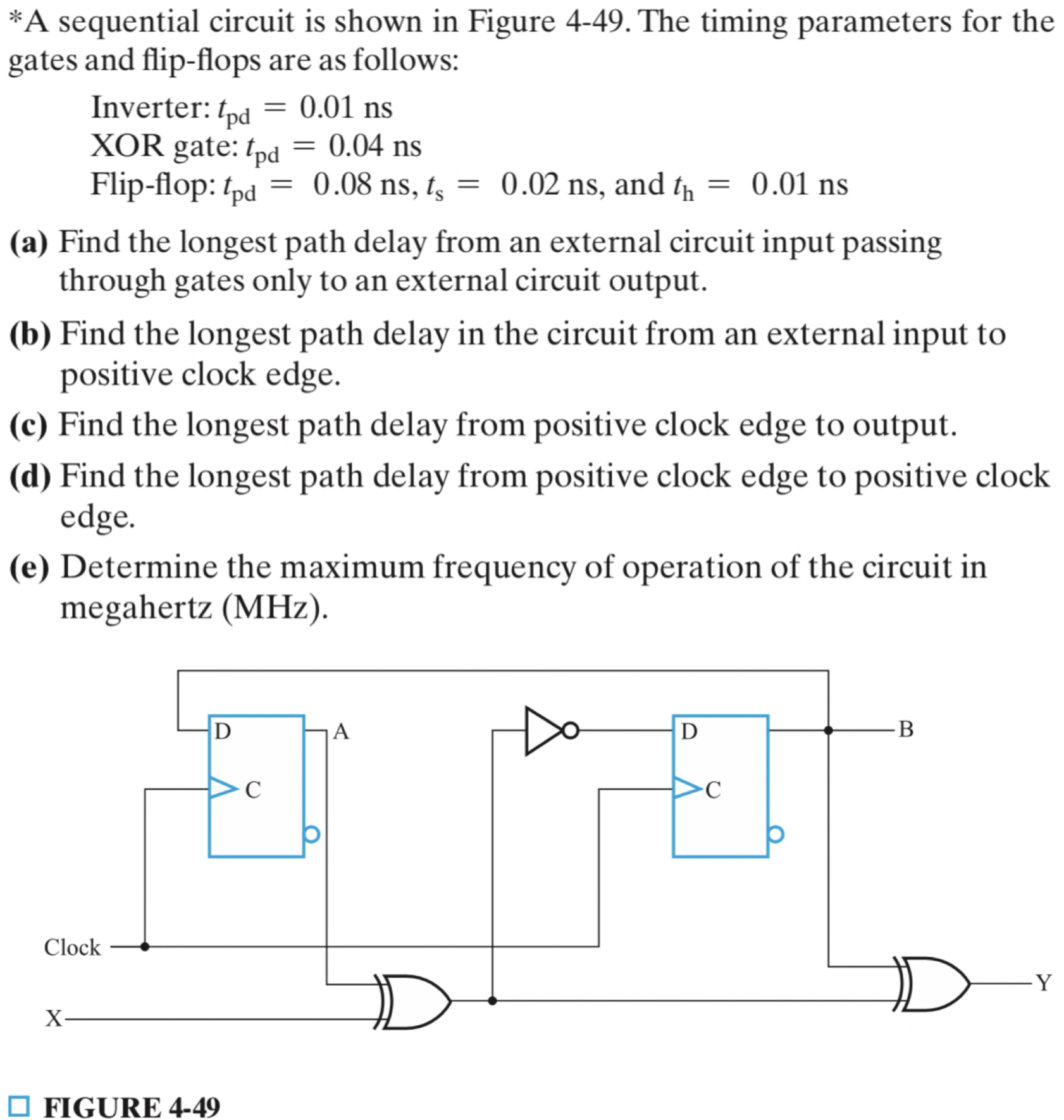
ROM 由 N 个输入，M* 个输出，以及 $2^{2N}$ 个译码后的最小项组成。

其中：

固定的 AND 用于设计译码器，实现所有的 $2^{2N}$ 个最小项；】
可编程的 OR 用于把这些最小项“或”起来并实现特定逻辑。】

严格来说，ROM 是不可编程的，PROM 才是可编程的。PROM(Programmable ROM) 通过 fuse 或 anti-fuse 等手段实现可编程，所以在出厂后仅可进行一次编程修改，属于永久编程技术。

ROM 可以被视作一个 memory，输入提供了一组地址(address)，而输出则是这组地址对应的 memory 中存储的信息。从这个角度来看，ROM 的确具有「只读」的特征。

eg

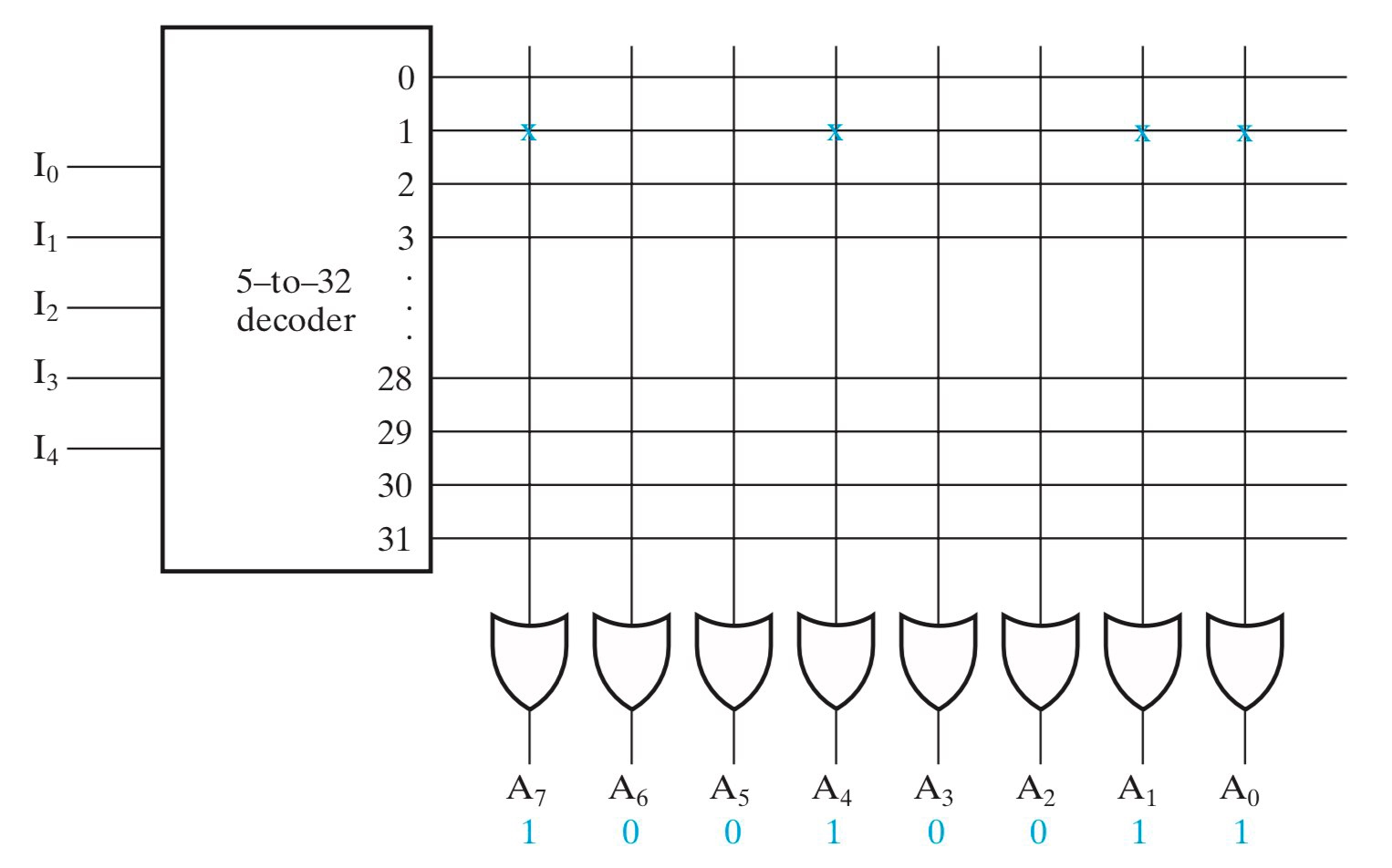
理解方式：译码器列出了$I_0-I_5$的所有最小项，然后每一个输出通过OR自主选择需要or一起的最小项

PAL

PAL 与 ROM 恰恰相反，其具有固定的 OR 和一批可编程的 AND。

PAL 不需要像 ROM 那样列出所有最小项，这就意味着 PAL 是可优化的，因此 PAL 在很多时候比 ROM 更高效更节约；
但也正是因为它不像 ROM 那样能够枚举最小项来实现所有逻辑，PAL 不一定能表达所有逻辑；
- 一种改进方法是，通过将一个既有的 PAL 输出当作输入，输入到另外一个函数中，来弥补项不足的问题，例如下图的W；

eg

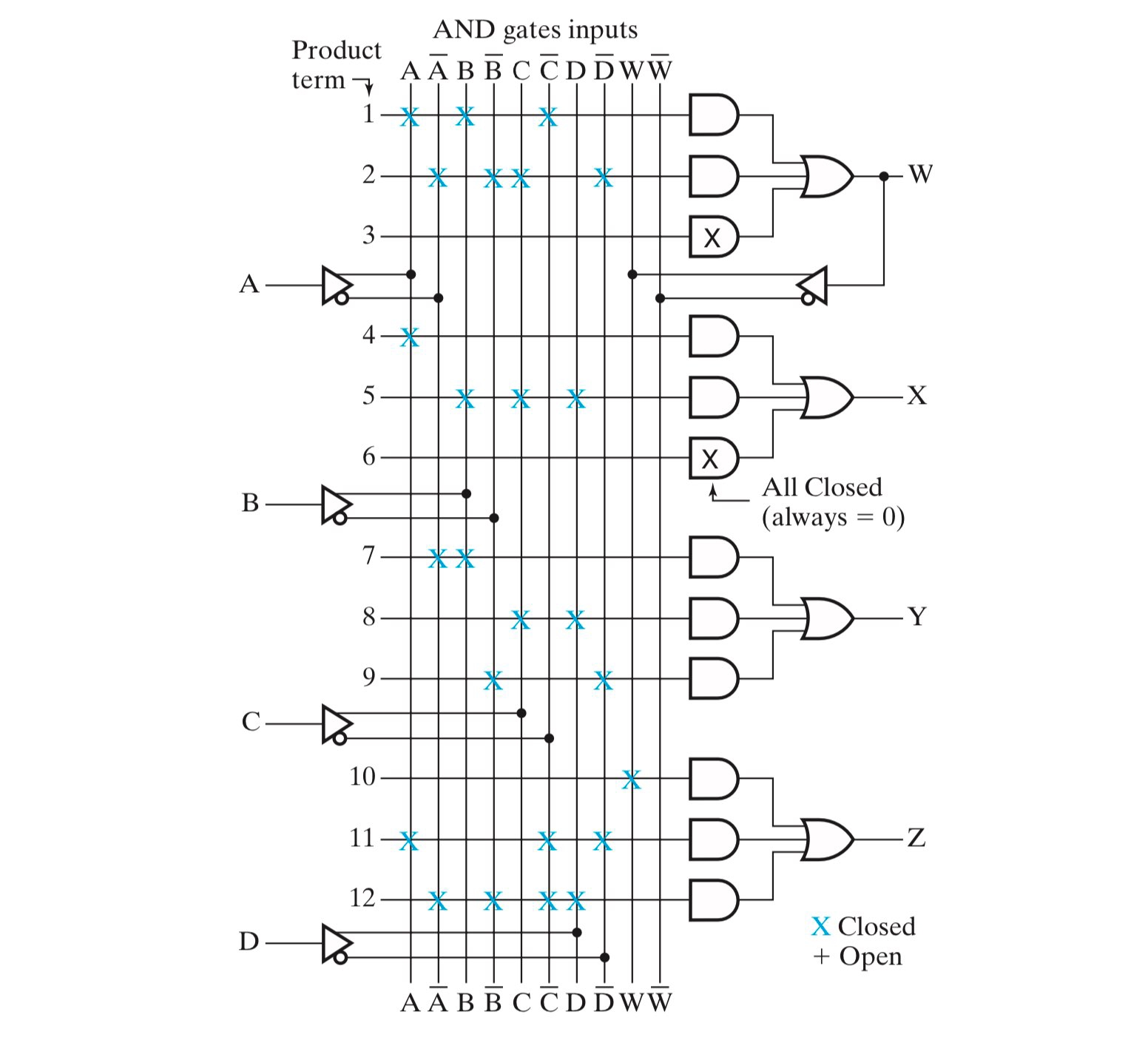
理解方式：列出每个输入的正负逻辑，通过AND自主选择这些来拼装成一个个最小项，再用OR将这些最小项or起来得到输出

PLA

PLA 在设计上和 ROM 类似，区别在于 PLA 并不使用译码器获得所有最小项，而是用可编程的 AND 阵列来代替译码器。

PLA 具有可编程的 AND 和 OR，因此比起 PAL 和 ROM 更具灵活性；
但是灵活性带来的弊端是，PLA 的优化会变得更加复杂，这对于优化软件有着更高的要求；
此外，PLA 和 PAL 具有一样的问题，就是无法表达所有逻辑函数；
- 一种改进方法是，在输出的时候再做一次异或（不用非门体现了可编程的思想），以产生新的项，来弥补项不足的问题；

eg

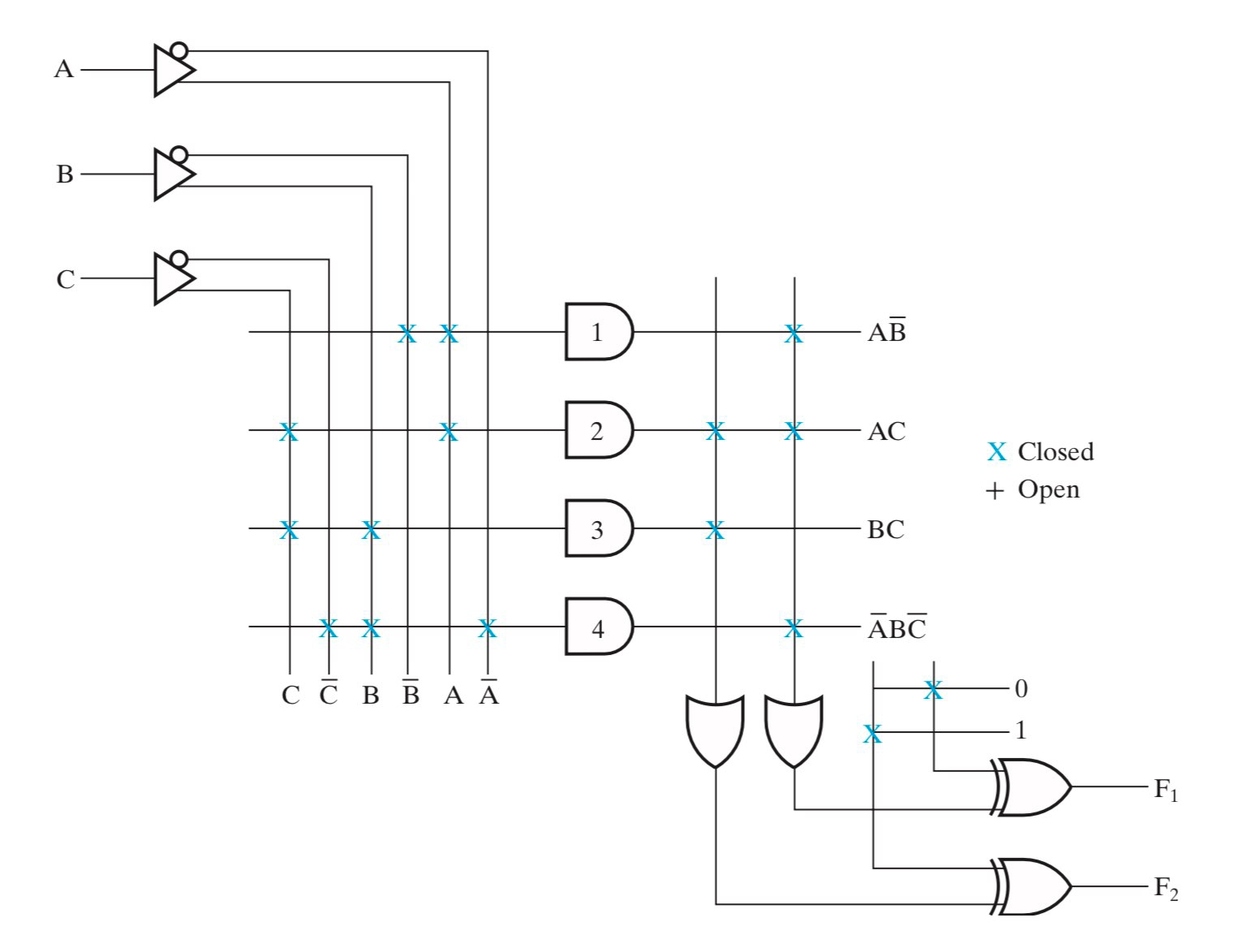
理解方式：左边部分借鉴PAL的方法通过AND组装成最小项，替换ROM中的译码器。右中部分即将最小项OR起来，同ROM的右半部分。

右下的抑或用于通过最小项之和转化为最大项之积，因为组装的最小项有限，通过取取反来获得更多种组合

Lookup Tables（查找表 LUT）

通过让数据源接内存，并通过修改真值表内的值，即修改内存里的值，来实现数据源的变化，来改变 MUX 的行为。

由于 LUT 存的本质上是真值表，所以它可以实现任意输入符合要求的逻辑函数。

所以，问题就变化为如何用较小的 LUT 来组合实现复杂的逻辑函数。

LUT 的基本结构如下：

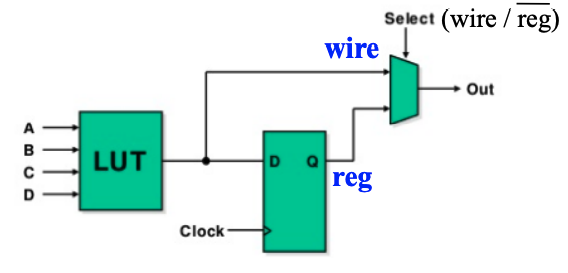
FPGA 的基本结构如下：

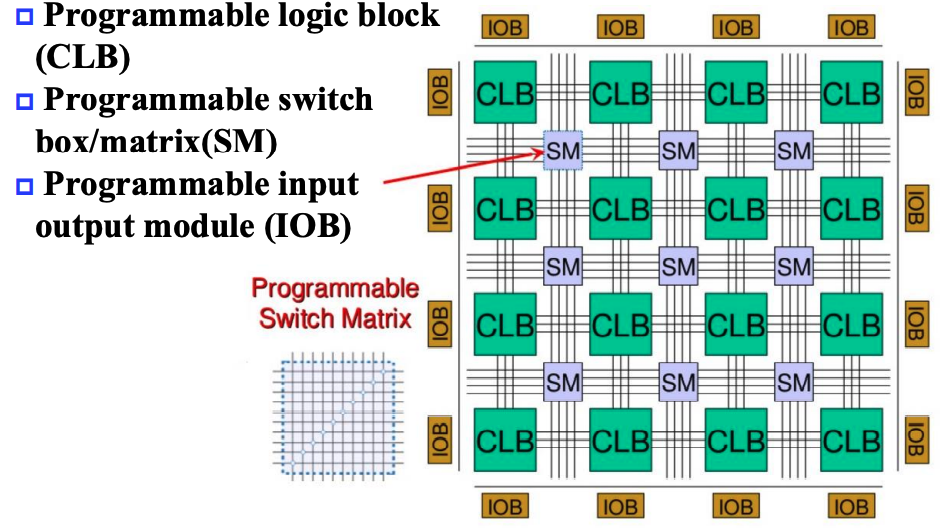
其主要分为三个组成部分：

CLB(Configurable Logic Block)
- 大量存储 LUT
SM(Switch Matrix)
- 可编程的交换矩阵
IOB(Input & Output Block)
- 可编程的输入输出单元

CLB

CLB 是 FPGA 中的基础逻辑单元。

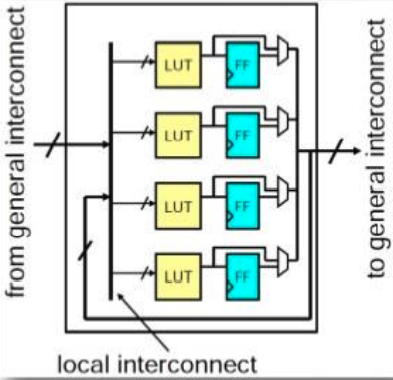
SM

通过相当复杂的算法， SM 会根据目标逻辑，选择链接不同的 CLB 以实现复杂逻辑。

它具有这些基本属性：

Flexibility: 评估一条线可以连接到多少线；
Topology: 哪些线可以被连接到；
Routability: 有多少回路可以被路由；

IOB

IOB 用来对外部设备进行连接，用来控制输入和输出。

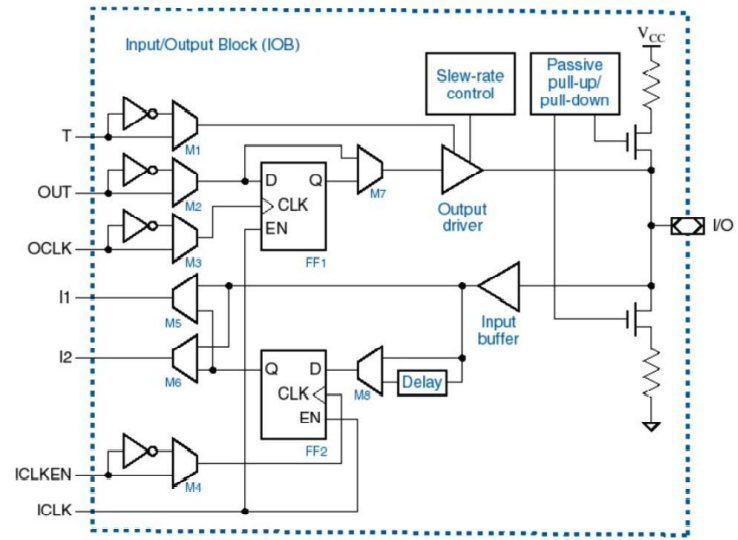
在软件层面编程完后，会生成位流文件(bitfile)，下载到板时会更新 FPGA 中的内容。

✒组合函数的实现方法

到目前为止，不管是可编程还是不可编程，都已经介绍了很多方法，这里进行一次小结：

Decoders & OR gates：将译码出来的需要的目标组合都 OR 在一起；

MUXs：通过多路选择器实现任意逻辑函数；

ROM

PAL

PLA

LUT

Chap 6 Registers & Register Transfers

⛵引入
这一章可以视为是第四章的一个延续，主要介绍（基于寄存器的同步）时序逻辑设计(Sequential Logic Design)。

寄存器

寄存器(registers)粗略的来说就是一堆触发器以及对应的状态控制电路，用来实现多位数据的存储等操作。

其中有一种特殊的寄存器叫计数器(counter)，它的行为就是随着时钟周期不断在固定的状态序列中循环。更形象的，一般是实现自动的计数功能，像电子时钟那样。

实现寄存器一个最直白的想法就是公用控制线路和分列数据线路来控制多个触发器，如下图是使用 DFF 实现的一个 4-bit register：

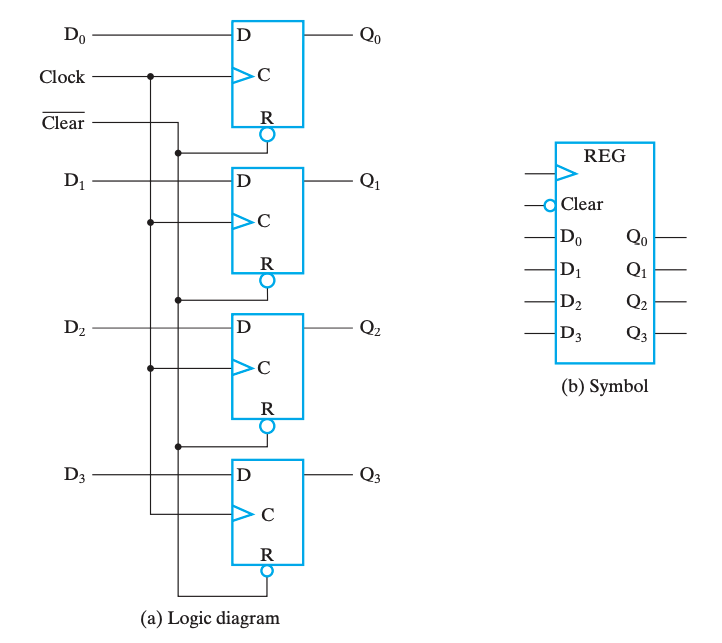
我们称新数据被写入寄存器的操作为载入(load)

如果载入操作在同一个时钟脉冲中完成，我们称之是并行(parallel)的。

保持

我们发现，如图的寄存器在每个时钟周期都允许载入。但是我们希望寄存器的载入能够被人为控制，也就是说当我们不希望载入数据的时候，寄存器能处于「保持」状态。主要有以下两种方案：

方案 A

其中一个做法是需要选择性的让它跟随时钟脉冲切换状态。做法就是将 Control 信号修改为$C=\overline{Load}+Clock$ ，如此而来，当$Load=0$时，始终有 $C=1$，脉冲消失，寄存器无法被载入。如下图，这种技术叫门控时钟(clock gating)。

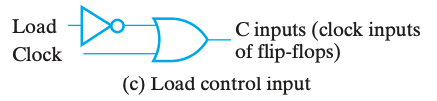
☠ clock skew

在门控时钟技术中，由于添加了一个额外的逻辑门，时钟脉冲到达 Control 的时候会出现额外的传播延时，即时钟偏移(clock skew)。

这微小的延时会导致在整个同步系统中，不同组件得到的时钟脉冲有偏差，而这是我们所不希望看到的。所以在实际设计中，我们应当避免或尽可能缩小时钟偏移。

方案 B

在不希望它修改的时候，不断将它的输入载入，也就是保持不变。

我们可以通过一个 MUX 来实现这个功能，用 EN 使能端来选择是载入新值还是保持之前的值，如下图。

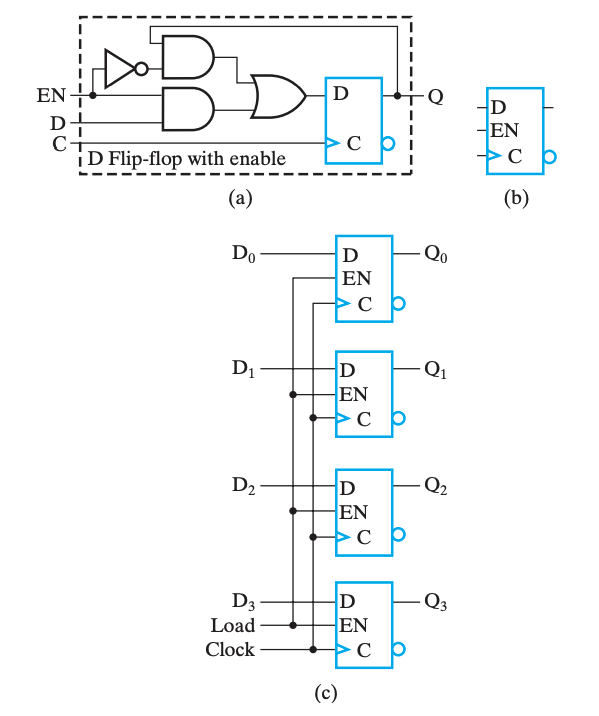
寄存器单元

⛵小节导读

本小节在书本中的位置靠后，但是考虑到内容的连续性我决定提前，本节内容会涉及一些之后的内容，实际上的绝对性知识较少，可以粗看过留下印象即可，大部分知识需要通过案例分析和实践获得，是类似于设计指导思想的内容。

寄存器单元(Register Cell)是寄存器的个体单元，主要包括一个 FF 及实现其组合逻辑的组合电路。

Register Cell Design

设计寄存器（尤其是大规模的寄存器）的重要手段之一，就是寄存器单元设计(Register Cell Design)。通常遵循以下步骤：

设计具有代表性的寄存器单元；

复制并连接若干个这样的寄存器单元；

修改某几个寄存器单元（通常可能是一串寄存器的首尾两个单元）以解决一些特殊情况或边界问题；

设计寄存器单元时，我们需要对寄存器单元进行定义。而指定(Specify)一个寄存器单元的功能的主要有这些方面：

寄存器的功能函数；
- 一般指寄存器传输；
控制信号构成；
- 有哪些控制信号、是否编码、如何决定是否 Load 等；
寄存器的输入数据；
- 有哪些输入数据、是否需要预先处理等；

在实际实现时，分为 MUX 实现和时序逻辑实现两种方法。

前者就是通过先分别实现逻辑，然后经由 MUX 选择相应的数据输入来实现。

后者按照时序电路的设计方法，确定状态图后根据状态变化设计时序电路，设计优化决定状态转移方程实现，具体可以参考第四章#时序电路设计。

寄存器传输(transfer)

把 transfer 翻译为“传输”是我脑瓜一拍的行为，我并不知道翻译成什么比较合适，如果读者有更好的翻译，请告诉我！

一个复杂系统除了信息的存储还需要信息的传输和处理，换句话来说，为了实现灵活、复杂的计算，我们需要信息之间能够广泛地交互。

大部分电子系统设计中，都会有一个控制单元(Control Unit)来负责指挥数据通路(Datapath)进行数据处理。

对于寄存器自身而言，它可能实现载入(load)、清空(clear)、移位(shift) 和计数(count) 等。

此外，对于那些寄存器中的数据进行移动了的加工，被称为寄存器传输操作(Register Transfer Operations)，它们主要包含这三个部分：

系统中的寄存器集合；
对于数据的操作；
监督操作序列的控制；

其中，最基础的那部分操作被称为微操作(microoperation)，它们是实现复杂操作的基础，例如将 R1 的数据载入 R2，将 R1 和 R2 相加，或是自增 R1 等。它们通常是以比特向量为载体并行实现的。

寄存器传输语言（Register Transfer Language, RTL）

一种专注于行为逻辑的语言，用来描述寄存器传输中的逻辑行为

通常具有特殊功能的寄存器都会用其名称缩写大写表示，例如 AR(Address Register)，PC(Program Counter)，IR(Instruction Register) 或者更普通的 R2(Register 2)。

寄存器传输的实现

引入

如何实现寄存器所存储的数据之间的处理与交互是本章节的核心命题。

如果说微操作关注的是数据的处理，那寄存器传输则着眼于数据之间的交互。

换句话来说，如何把数据给到别的寄存器、如何获取别的寄存器给到的数据、如何传输和选择这些数据，就是本小节要解决的问题。

特别的，寄存器传输的实现可以直接实现转移操作。

基于 MUX 实现传输

对于一个单一寄存器，它的输入可能有多种来源，例如其它寄存器，又或者是其他操作的结果。

总而言之，它的输入很可能是不唯一的，而同一时刻我们只能接受一个来源的输入。

因此，我们需要使用 MUX 来对输入进行选择。

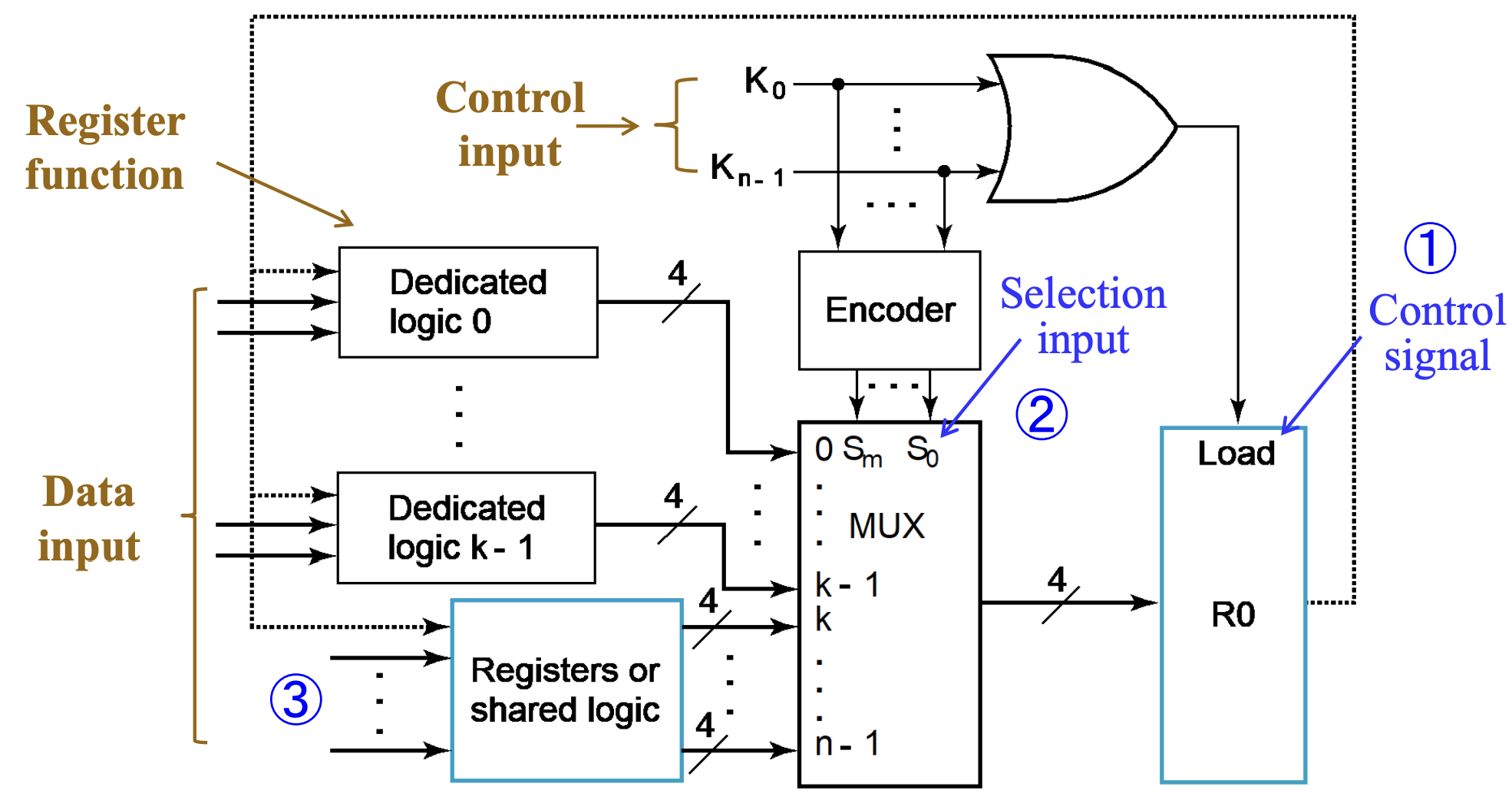
eg

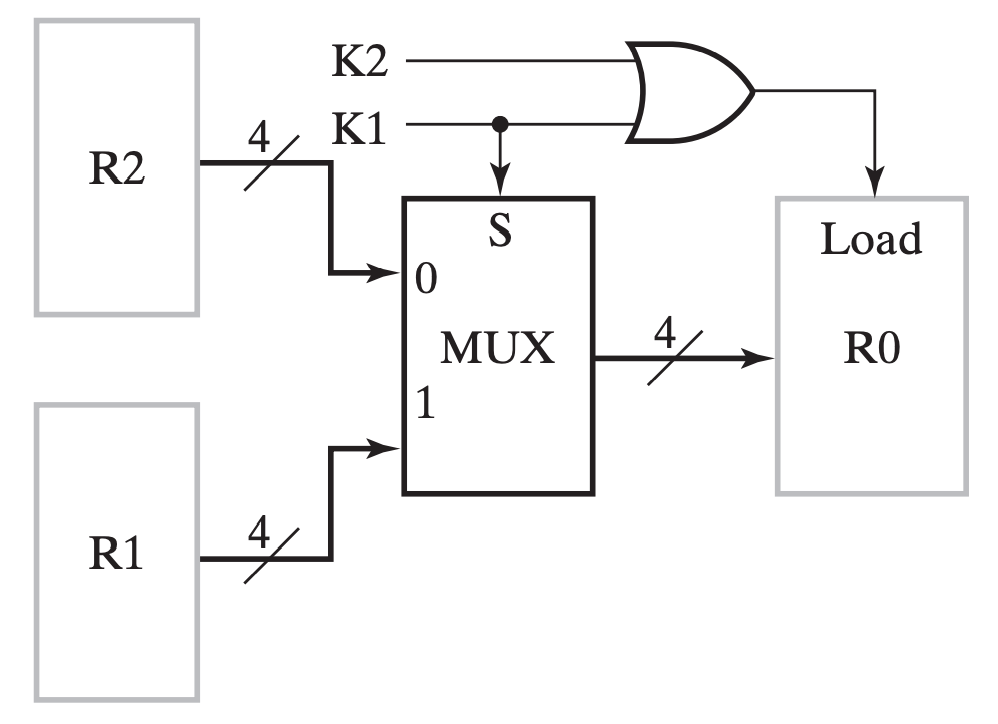
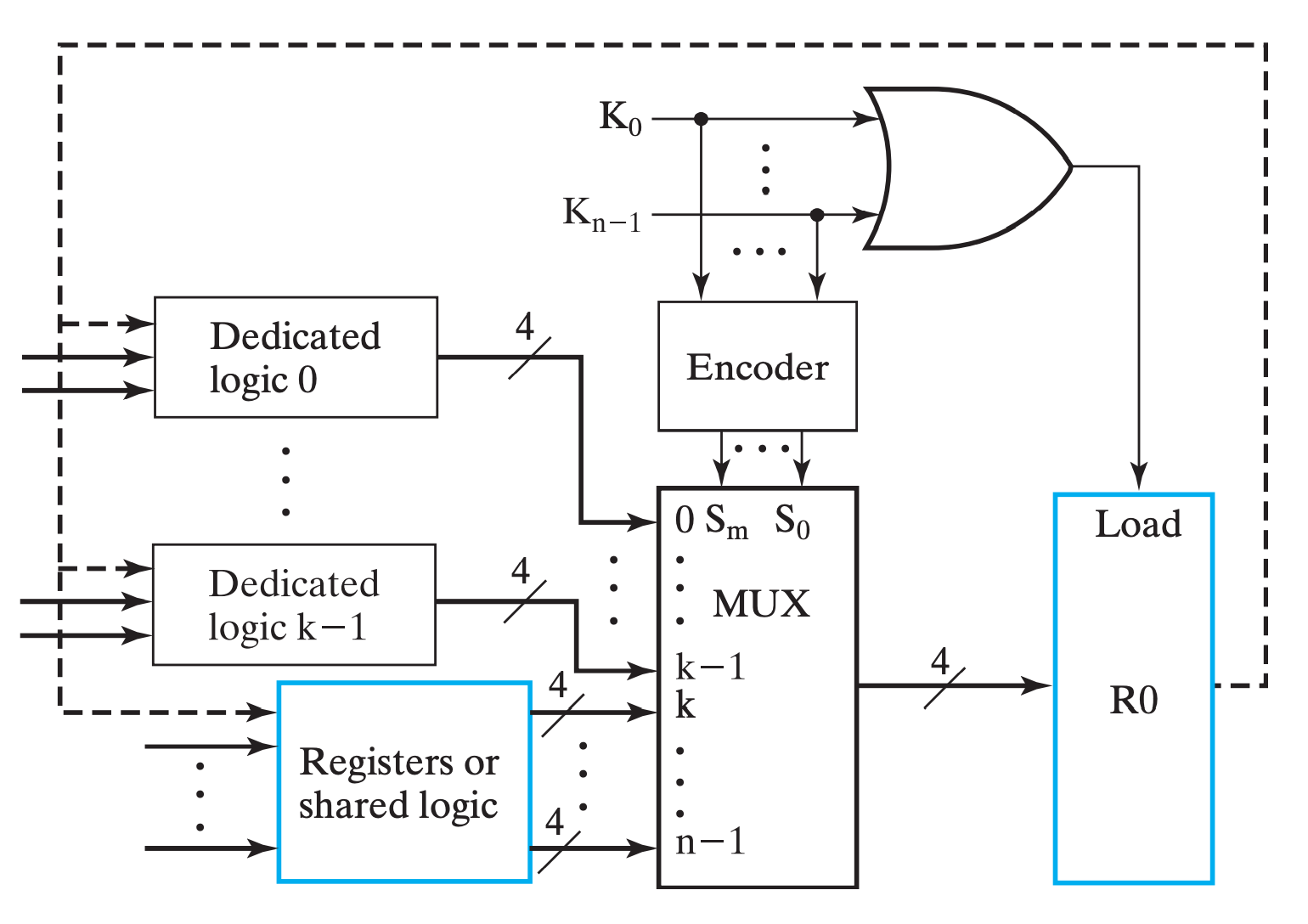
即，我们通过一系列 one-hot 编码（或者是 one-cold）来表示选择哪个输入源，通过 Encoder 将它们编码作为 MUX 的输入选择信号，从多个输入源中选择对应的源，并输出给目标寄存器；此外，将选择信号都或起来，作为目标寄存器的 Load信号

MUX 实现主要的实现了多对一的数据传输问题。如果我们单单使用 MUX 来完成寄存器之间的数据交互（假设所有寄存器都能相互传输数据），那将这个模型（图例在下一小节）抽象后，我们得到的将是一张“完全图”，然而它肉眼可见的开销大。

而总线则非常巧妙地优化了这个问题（并不是上位替代关系）。

基于总线(bus)实现传输

具体来说其实现方法有两种——通过共有 MUX 实现，或通过三态门实现。

共有 MUX 实现

eg

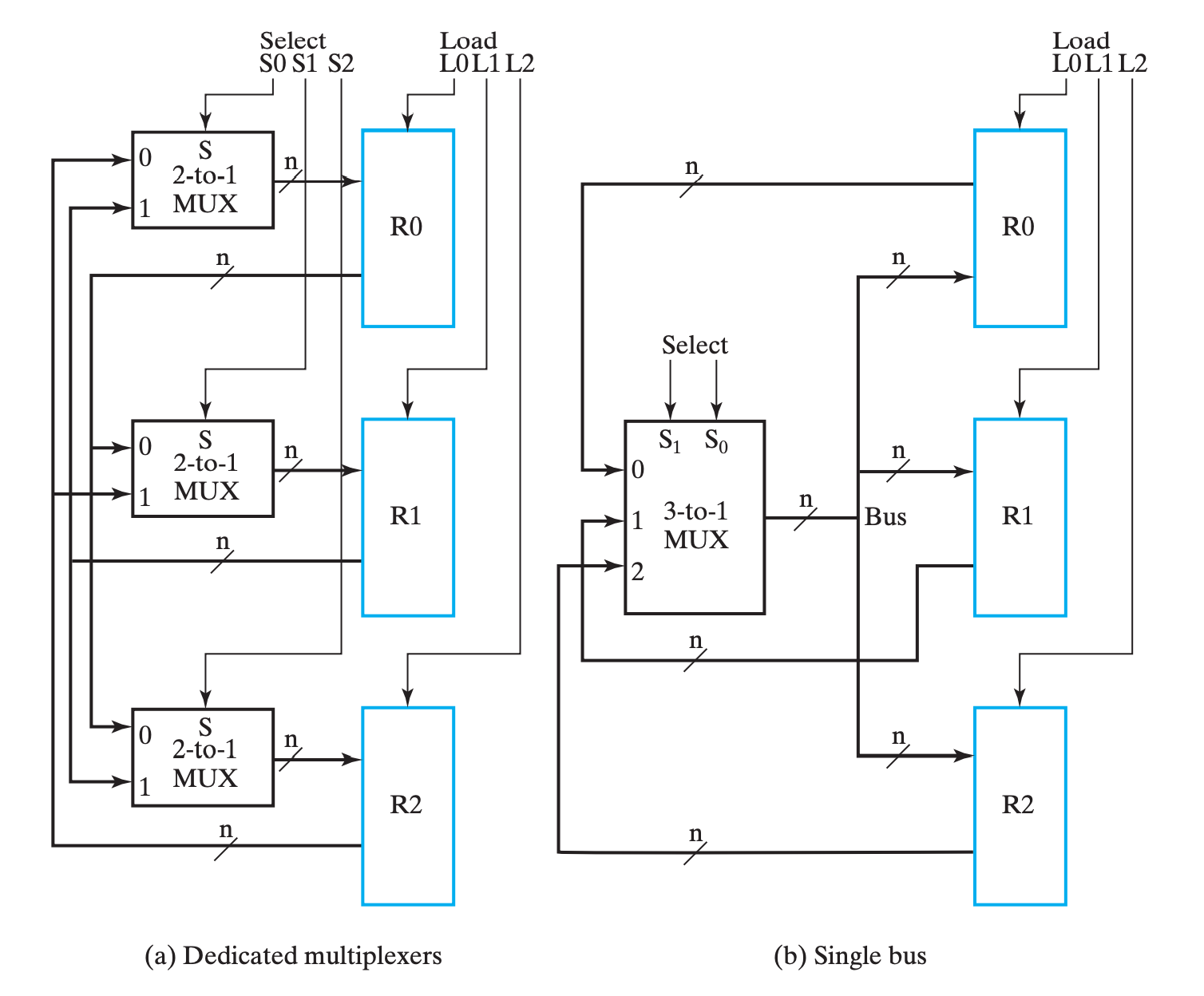
此时 MUX 不再是某个寄存器的专有逻辑(dedicated logic)，而是三个寄存器共同使用的共有逻辑(shared logic)。

总线中的 MUX 在所有寄存器的输入中选择其中一个，并将它输出，给到所有寄存器；而总线通过控制 Load 信号来选择让哪个（或哪些）寄存器得到这个信号。

与 MUX 实现对比

优势：

电路更精简，成本更低，随着寄存器增加这个特点更加明显；

劣势：

同一时刻内总线只能传输一个数据，即只有一个数据源(source)；

同一时钟周期内只有一个数据能传输到别的地方，例如交换操作就需要至少两个时钟才能实现；

三态门实现

只要我们让导线的若干输入中只有一个三态门不在「高阻态」，就能够优雅地实现多路输出互联。

实际上，所谓的三态门实现原理上和 MUX 实现无二，只不过我们是通过三态门来实现「路由」这个逻辑而已，也就是书上所说的：

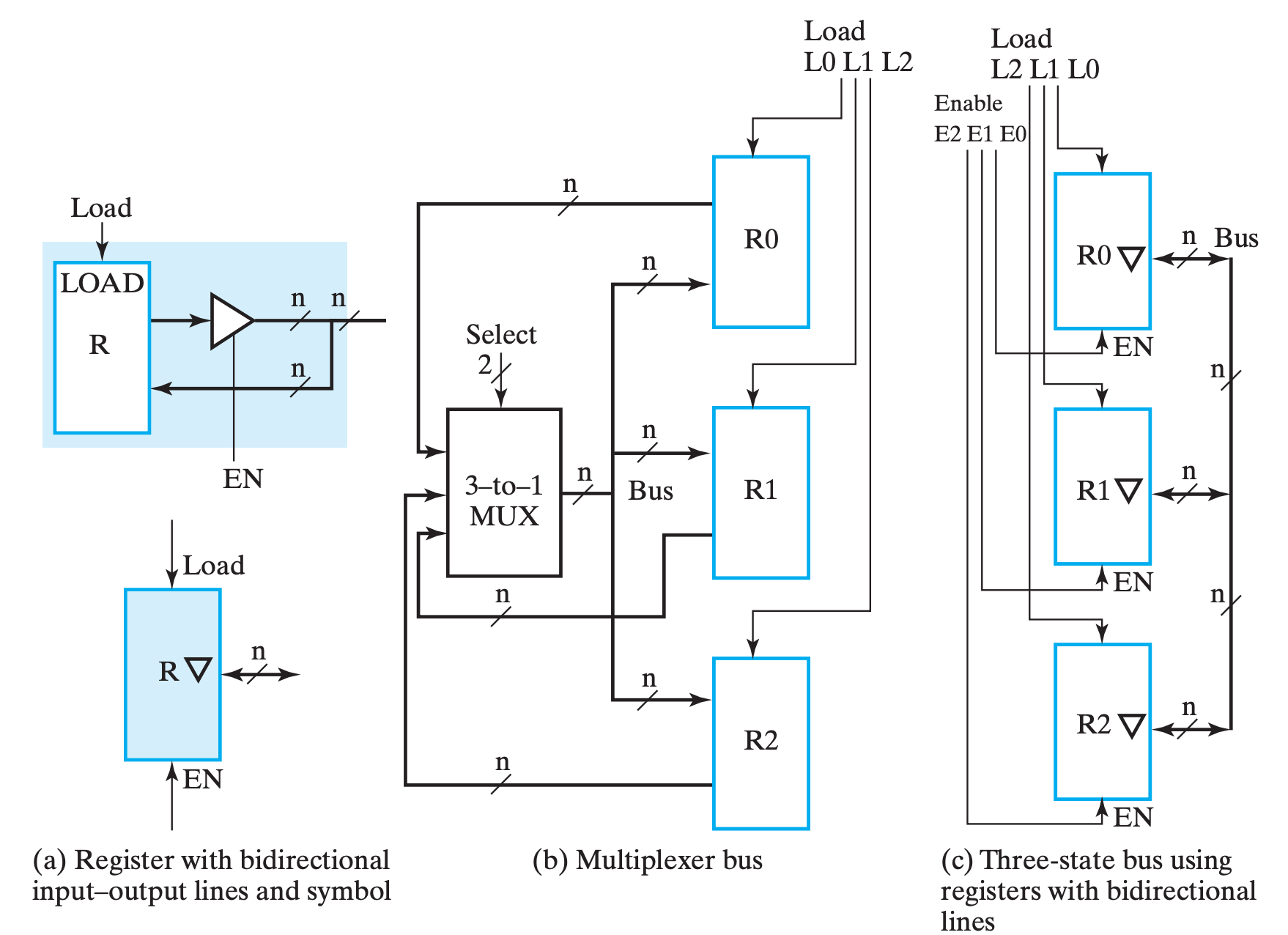
(c) 中对三态门的表示进行了简化，含义参考 (a)。

它想表达的主要含义是，当 EN 为 1 时，表示输出；反之表示输入（当然，真正决定是否读入寄存器的还是 LD）。

虽然书中说三态门的接线比 MUX 的少了一半，但我觉得三态门只是把线分岔的地方移动到了寄存器附近，换句话来说不如说是节省了导线的长度。但是随着输入的增加，MUX 的结构会越来越复杂且需要重新设计，但三态门只需要量的增加就行了，所以确实是更加吸引人。（当然，虽然书中没说，但是我觉得 Enable 必须 at most one-hot，而这部分的逻辑对于两个实现方法来说是一样的）

微操作及其实现

微操作一般分为这四种：

转移，transfer microoperations，将数据从一个寄存器转移到另外一个寄存器；
算术，arithmetic microoperations，对数据的算术运算操作；
逻辑，logic microoperations，对数据的逻辑运算操作；
移位，shift microoperations，对数据的移位操作；

转移

不改变数据本身，只是从一个寄存器中把数据移动到另外一个寄存器。

将 R0 中的数据转移到 R1 中，RTL表示为 $R0\leftarrow R1$

实现方式即寄存器传输

算术

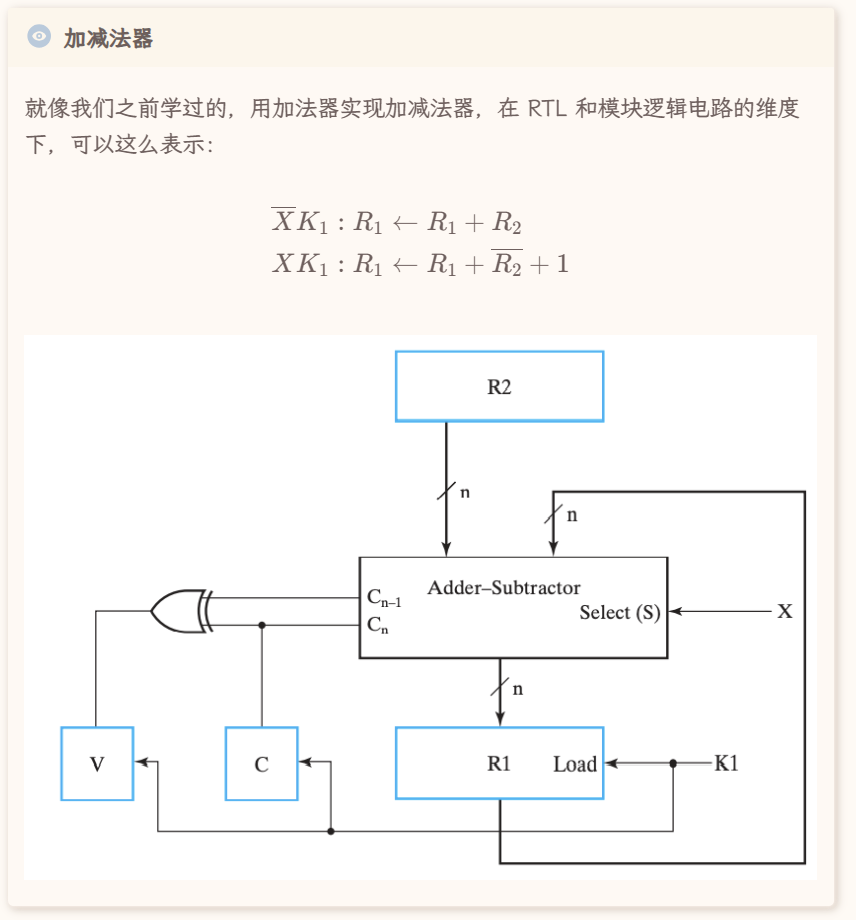
注意

对于如上出现的形式如：condition:reg←optionsoneregs 的表达式，: 左侧出现的 + 表示或，右侧的则表示加（“乘”也是这样）！

相对应的，加减法的实现可以通过加减法器实现，乘法可以用移位操作实现，而除法相对复杂。

逻辑

逻辑运算的实现相比算术更加直接，因为大部分逻辑都可以通过逻辑门来实现。

移位

移位的实现通过移位寄存器(Shift Register, SHR)实现。

引入

移位操作从本质上来讲，是通过触发器随着时钟脉冲，将串行数据一位一位地移动实现的。

串行实现

移位操作最简单的实现只需要与输入数相同位数的触发器实现。它的基本结构如下：

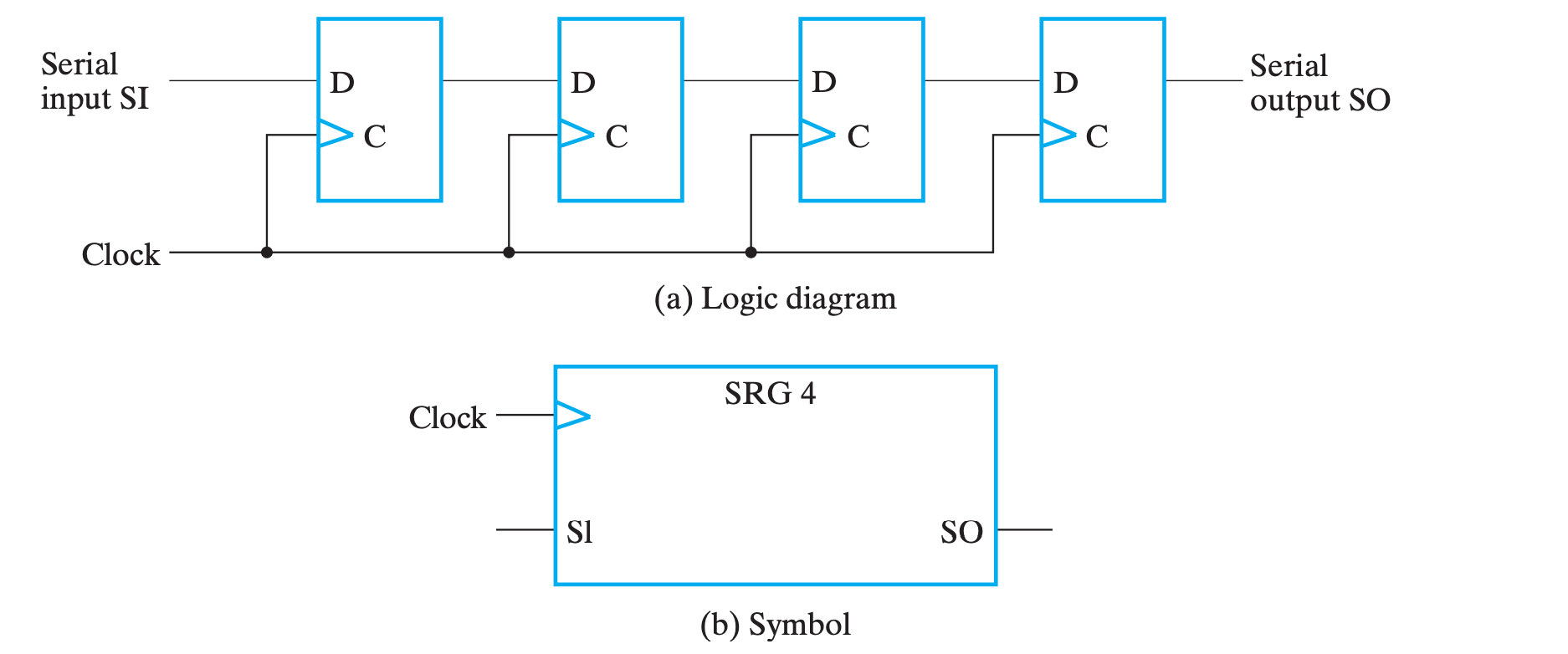
四个触发器首尾相连，最前面串行输入(Serial Input, SI)数据，末端得到串行输出(Serial Output, SO)，在不同时钟周期的偏差下，连续读入的 n bits 即为不同位数移位的结果。

并行化

并行化主要有两个方面，即并行输出(parallel output)和并行载入(parallel load)，分别对应着在同一个时间周期内得到每一个 FF 的结果和对每一个 FF 载入数据。

并行输出的实现非常简单，只需要给每一个 FF 的输出引出一条线就行了，它与串行输出可以直接同时存在；而并行输入则与串行输入冲突，一次只能实现其中一个，所以需要一些控制电路：

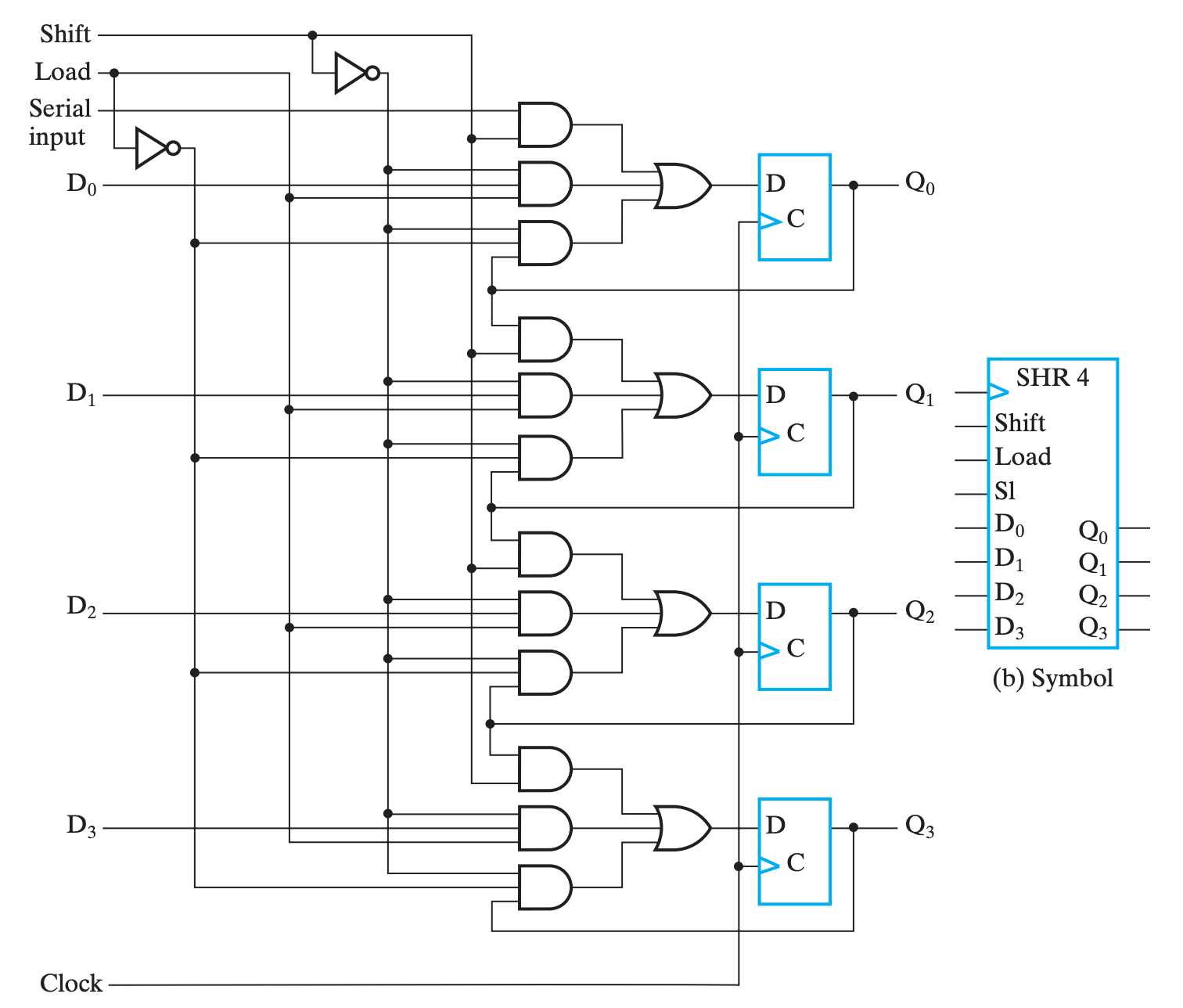
看起来有点复杂，但是实际上逻辑还是很清晰的。

纵向观察右侧的四个 FF，可以发现基本上就是串行移位实现，只不过其输入不再是直接从上一个 FF 那边拿来的；
四个 FF 的输入是类似的，所以我们仅关注最上面的那三个与门和一个或门，表示数据输入有三个可能的来源；
1. 第一个与门， $F_i=Shift\cdot SI$（对于后面几个 FF ，则是$F_i=Shift\cdot FF_{i-1}$），可以发现，此时电路的行为与串行移位实现一致；
  - 即 $Shift$ 为 1 时，SHR 表现为「每个周期执行一次移位」；
2. 第二个与门，$F_i=\overline{Shift}\cdot Load\cdot D_i$ ，此时电路的行为是使用比特向量对每一个 FF 赋值，即并行载入；
  - 即 $\overline{Shift}\cdot Load$ 为 1 时，SHR 表现为「并行载入」；
3. 第三个与门，$F_i=\overline{Shift}\cdot \overline{Load}\cdot Q_i$ ，此时电路的行为是保持上一周期的结果；
  - 即 $\overline{Shift}\cdot \overline{Load}$ 为 1 时，SHR 表现为「保持」；

总和来说，就是： $$ Shift:Q\leftarrow slQ\ \overline{Shift}\cdot Load:Q\leftarrow D\ \overline{Shift}\cdot \overline{Load}:Q\leftarrow Q $$

双向移位寄存器

上面介绍的移位寄存器随着时钟周期的供给，只能不可逆、单向地进行移位，这种移位寄存器称为无向移位寄存器(Unidirectional SHR)；

对应的，如果能够支持可控制的左移右移，则被称为双向移位寄存器(Bidirectional SHR)。

其行为如下：

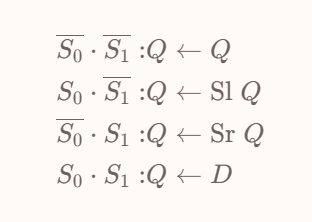
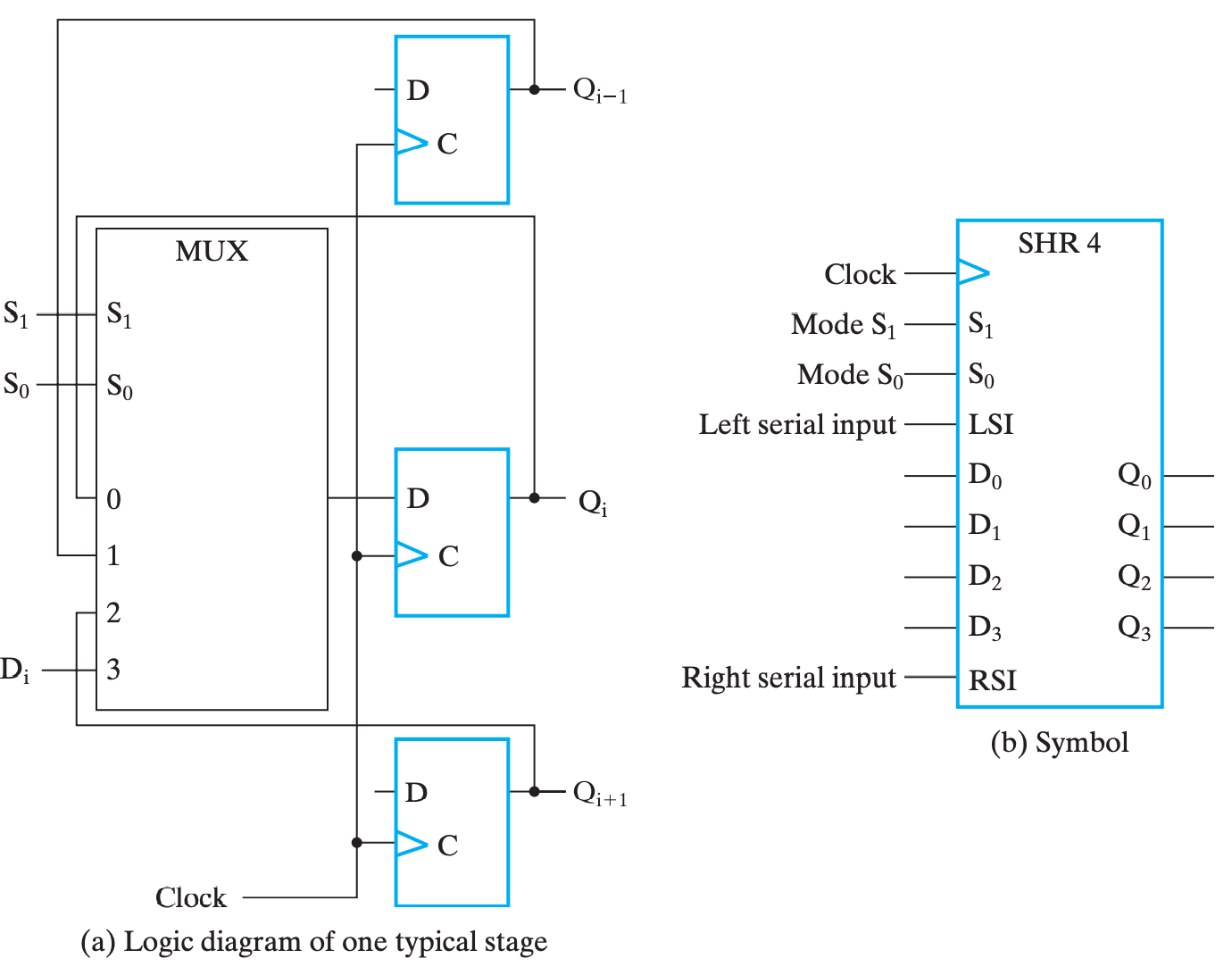
其本质上就是添加了一个 MUX 来选择下一个时钟是继承 $(i+1),(i-1),D_i$ 还是 $Q$。

代码意义上的移位一般指的是一个双目操作，即可以指定移位多少位，这个参数被称为移位量(Shift Amount)。

计数器

根据实现原理，主要分为 行波计数器(Ripple Counter) 和 同步计数器(Synchronous Counter) 两种。

行波计数器

行波计数器的主要思想就是将一个不断自反的 FF 的输出直接或间接作为下一个 FF 的时钟脉冲。由于形成一次脉冲需要一对 0&1，所以前一个 FF 取反两次才能引起下一个 FF 取反一次，

如果下一个 FF 是在上一个 FF 的输出从 1 变 0 时触发，那两个 FF 的变化刚好对应于二进制自增的进位规律：(0,0)，(0,1)，(1,0)，(1,1)，(0,0)，...

于是，一个 4-Bit 行波计数器的逻辑图就如下：

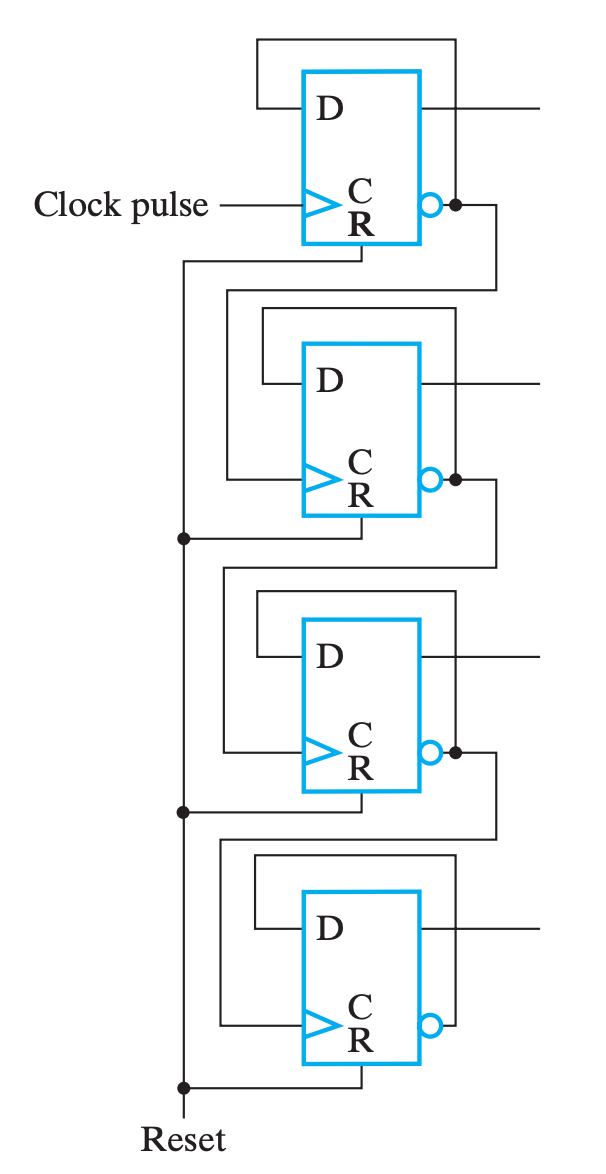
上图中，下一个 FF 的时钟来自于上一个 FF 的输出取反，也就是对于上升沿触发的 FF 来说，下一个 FF 会在上一个 FF 的输出从 1 到 0 时自反，所以是正向计时(Upward Counting)；

反之，如果下一个 FF 的时钟来自于上一个 FF 的直接输出，也就是对于上升沿触发的 FF 来说，下一个 FF 会在上一个 FF 的输出从 0 到 1 时自反，所以是逆向输出(Downward Counting)；

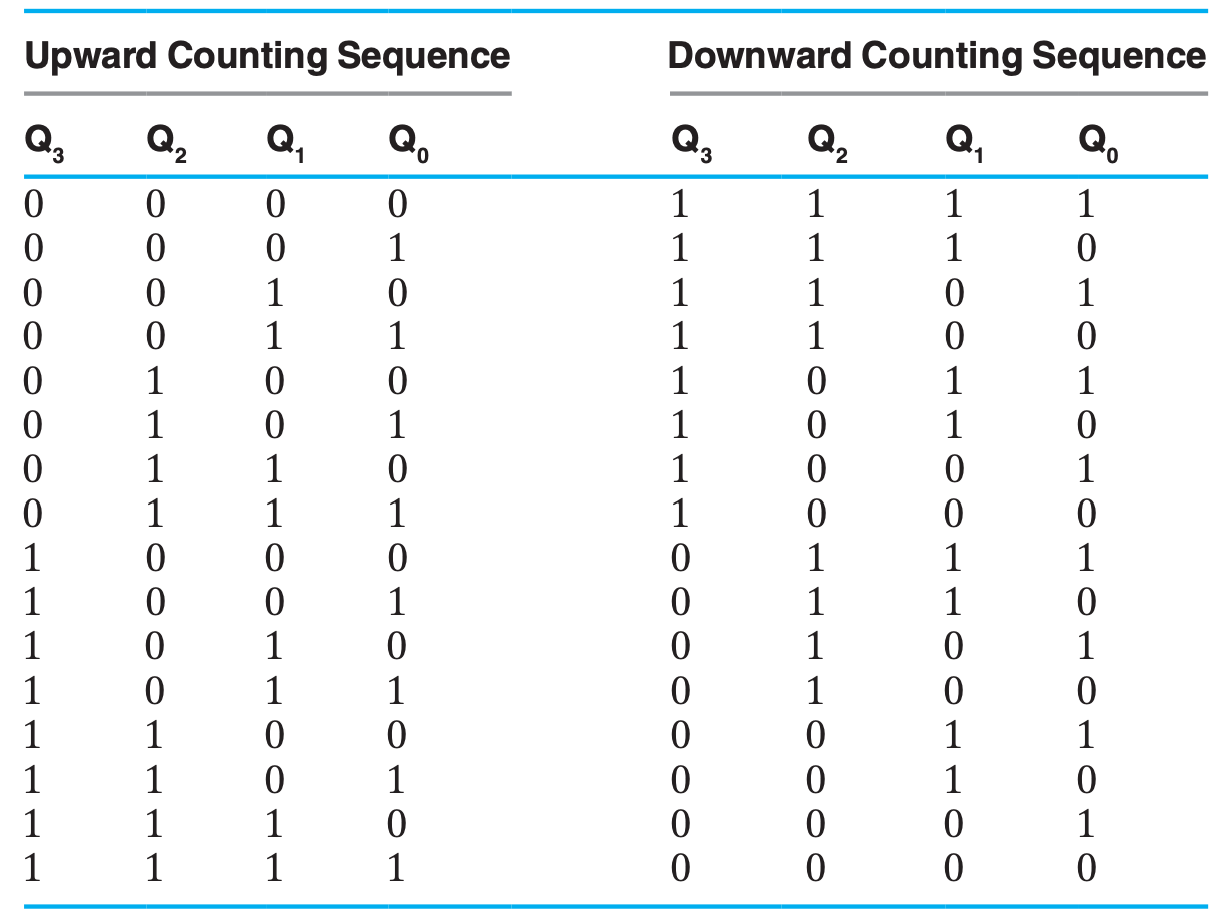
行波计数器的优点是电路简单，成本低；

但是缺点也很明显，既然它与同步计数器相区分，就说明它不是同步电路，每一个 FF 都会有传播延时，随着计数范围增大，总传播延时也会增加，而为了让电路正常工作，时钟频率也要因此下降。

多数情况下行波加法器只会在低功耗电路中被采用。

同步计数器

同步计数器从实现自增的原理上来说，和行波计数器也是类似的，同样是在上一个 FF 完成一次翻转的时候让下一个 FF 变化。

只不过同步计数器不是控制时钟，而是控制「FF 内的值是否取反」来实现，而它是通过异或门来实现的。

我们知道，$0 xor X=X,1xorX=\overline X$ 。因此，我们可以控制 XOR 的某个输入是 0 还是 1 来实现取反还是保持的切换。

需要区分的是，行波计数器是在上一个 FF 变化完才影响下一个的，所以是 1 变 0 时需要进位；

而同步计数器的所有 FF 是一起变化的，所以只有在前面都是 1 时候，表示下一刻它们都要进位了，当前 FF 才进位。

也就是说，行波计数器是建立在前一个 FF 的结果进行变化；而并行加法器是建立在上一刻所有关联 FF 的状态，对下一状态的预判。

在这基础上，同步计数器的自增器(incrementer)有两种不同的实现方法：

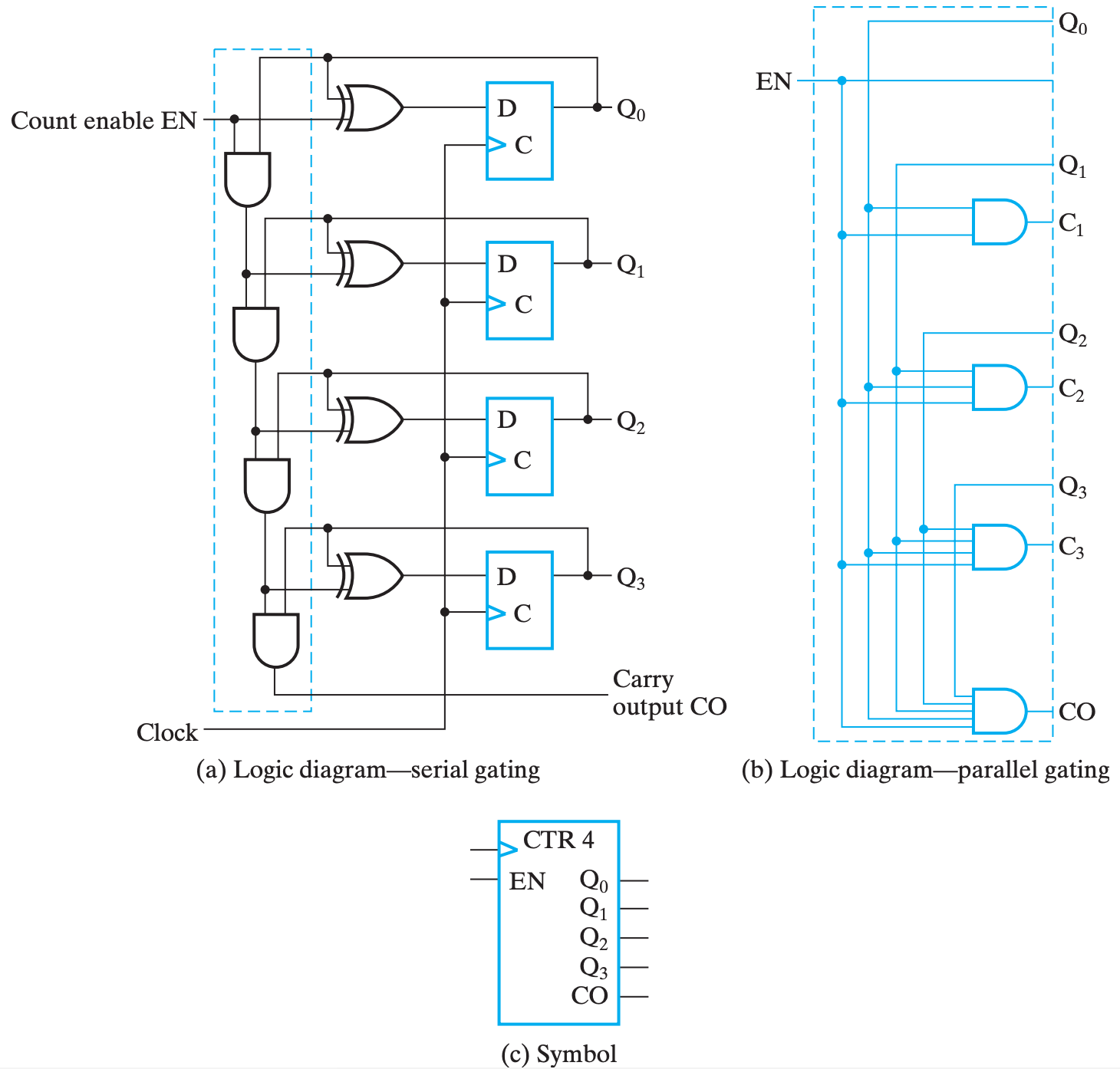
(b) 的蓝色部分替换 (a) 的蓝框部分为第二种。两种分别为门串行实现和门并行实现。

两种实现其实原理都是一样的，

只不过门串行牺牲某些情况下的运行效率，节约了门成本；

而门并行提高了门成本，减少了某些情况下的门延迟。

当然，既然使用的是自增器，那么实现的自然就是正向计数器。为了实现逆向计数器，我们则需要将自增器换为自减器。做法只不过是将异或门的控制信号取反。

具体来说，兼具自增自减功能的输入函数如下：

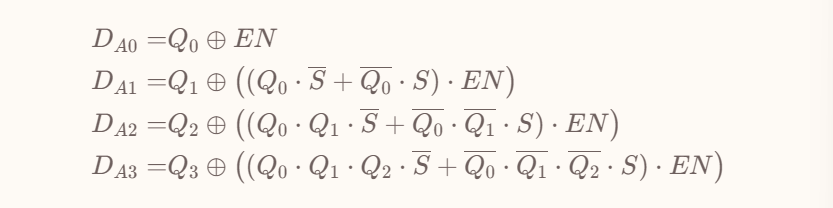
这个表达式也可以略微感受到门串行和门并行的区别究竟在哪里，它们使用同一个表达式，只不过用不同的方式来实现多位 AND 运算。

同步载入

这里同步载入的含义可以同移位寄存器的并行载入类比，其主要目的是将计数器的当前值设为一个我们需要的数字。

以门串行实现为例，添加功能控制逻辑后的设计如下：

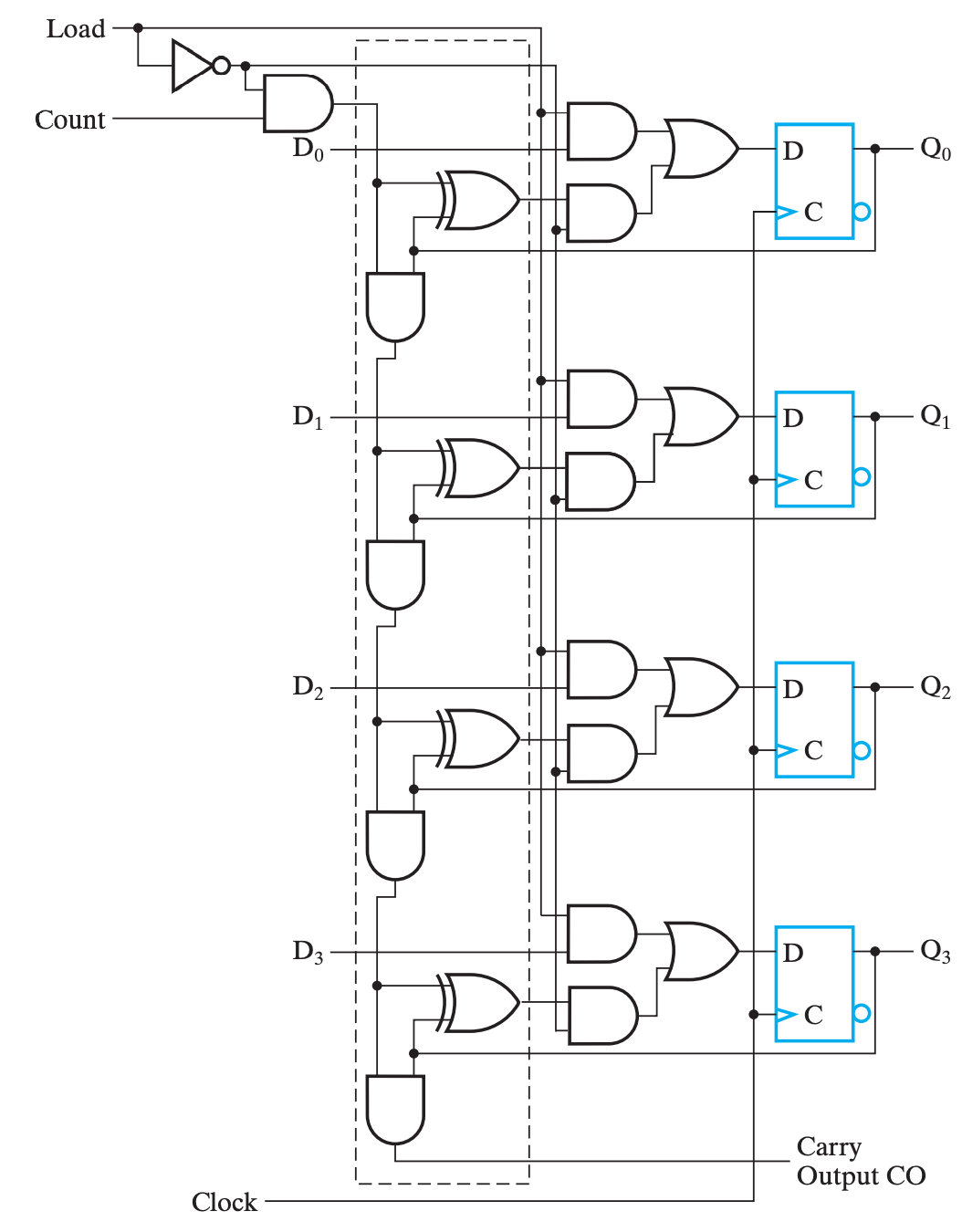
任意计数序列

现在让我们回归计数器的行为：随着时钟周期不断在固定的状态序列中循环。也就是说，这个序列未必需要是整数自增自减序列。而实现某一序列的计数行为，实际上只要设计好有限状态和状态之间的转移即可。

当然，这个话题太过宽泛，我们在这里具体讨论的还是整数自增序列，只不过限制了上下界。书上提供的案例是 BCD 码的循环计数，那我们也跟着这个案例来。

BCD 码循环计数

首先我们需要根据时序电路的设计规则，搞清楚状态序列，显然，根据 BCD 码的定义，我们可以毛毛地认为它是下确界为 0，上确界为 9 的 4 比特整数序列。换句话说，我们需要实现一个计数到 9 后下一个状态是 0 的 4 比特计数器。

于是我们可以当计数器的输出为 9 时，下一周期让计数器载入 0：

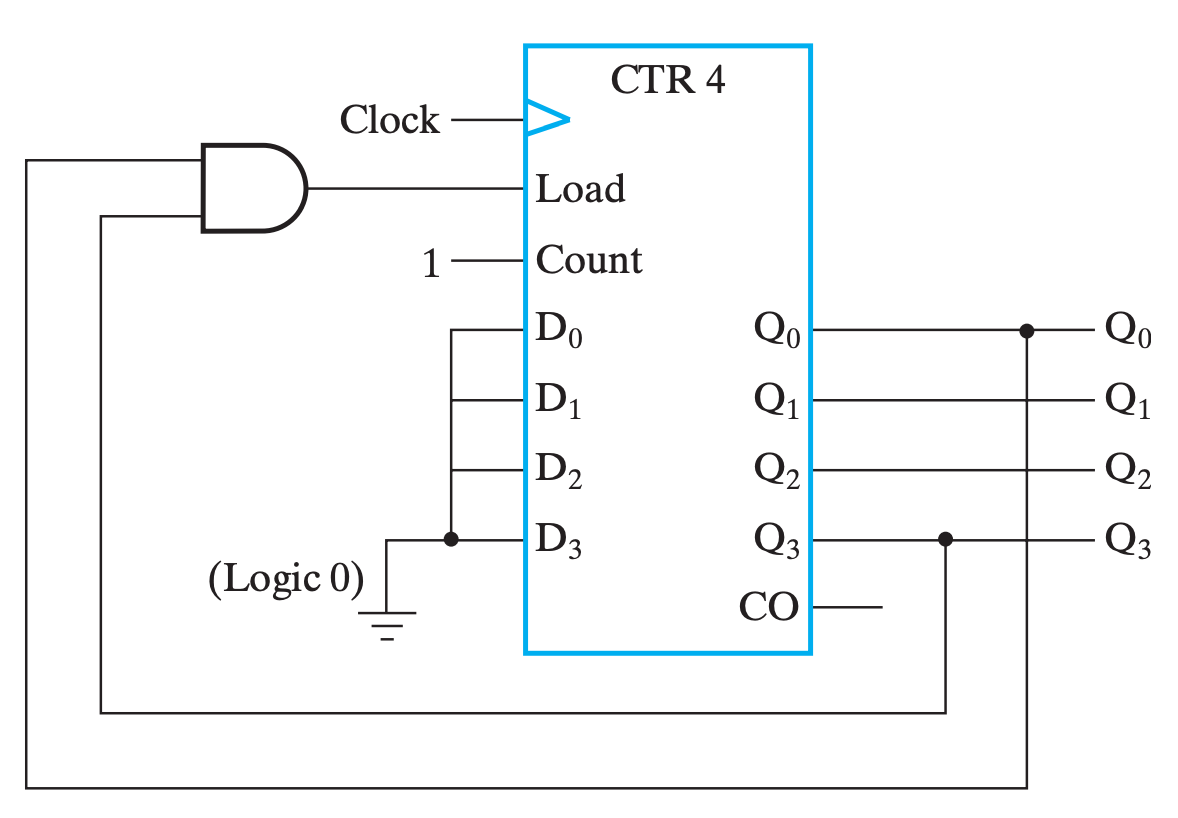
按理来说这里应该是 $Load=Q_0Q_1nQ_2nQ_3$ ，以对应 9D=1001B，但是由于自增过程中，1001 是第一个满足 1??1 的组合，所以可以直接简化为 $Load=Q_0Q_3$

Mod N 计数器

实际上，我们可以把 BCD 码循环计数器看作是特殊的 Mod N 计数器，即 N = 10 的 Mod N 计数器。

或许你会想，实现 Mod N 计数器能不能在满足输出条件后直接使用 Clear 输入。但是请不要忘记了，Clear 也好，Set 也罢，它们都是异步操作。我们没有必要也不应该使用异步操作，所以最好的做法还是使用 Load。

寄存器传输的控制

寄存器传输系统(Register Transfer System)设计流程：

确定系统的行为(specification)；
定义外部的输入、输出，以及控制单元(control unit)和数据通路(datapath)需要的寄存器；
设计状态机；
定义内部的控制信号、状态信号；
- 用这些信号来分配输出条件(output condition)、输出行为(output actions)等，包括寄存器传输(register transfer)（个人理解是设计内部信号来进一步设计状态机，包括设计 TC、OC、OA 等）；
绘制框图(block diagram)；
设计控制单元和数据通路的寄存器传输逻辑(register transfer logic)；
设计控制单元逻辑(control unit logic)；
验证正确性；

我们在 第三章 介绍了组合逻辑设计的基本流程，而这里的寄存器传输系统，实际上是（基于寄存器的同步）时序逻辑设计的基本流程。这个流程看起来比较抽象，但总体思路和组合逻辑设计其实是一致的。重要的是结合具体例子去实践这个设计流程，建议阅读教材中相应位置的 DashWatch 和 Handheld Game: PIG 这两个例子。

Chap7 存储器

Memories

Memory is a collection of binary storage cells together with associated circuits needed to transfer information into and out of the cells.

Two types of memories are used in various parts of a computer: random-access memory (RAM) and read-only memory (ROM).

ROM-只读存储器

RAM can perform both the write and the read operations, whereas ROM performs only read operations. RAM sizes may range from hundreds to billions of bits.

Memory Organization

The memory is organized as an array of storage cells, each of which is capable of storing one bit of information.

The cells are arranged in rows and columns. The intersection of a row and a column is called a memory address. The number of rows and columns determines the capacity of the memory.

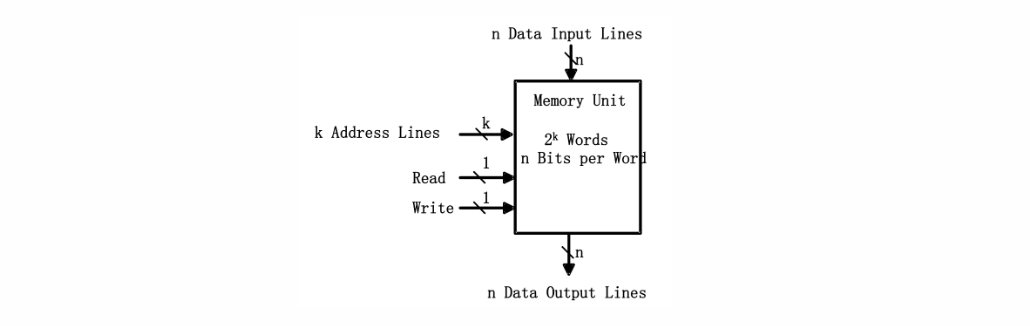
memory organization

RAM

Memory cells can be accessed to transfer information to or from any desired location, with the access taking the same time regardless of the location, hence the name random-access memory.

In contrast,serial memory, such as is exhibited by a hard drive, takes different lengths of time to access information, depending on where the desired location is relative to the current physical position of the disk.

RAM-Random Access Memory (RAM)

随机访问存储器

访问时间与访问位置无关系。相对的有顺序存储器，如磁带

RAM分为两种：static RAM (SRAM) and dynamic RAM (DRAM)。

SRAM是静态的，DRAM是动态的。SRAM的速度比DRAM快，但是DRAM的容量比SRAM大。

SRAM的单元是由flip-flop构成的，DRAM的单元是由capacitor和transistor构成的。（每隔一段时间需要refresh）

SRAM

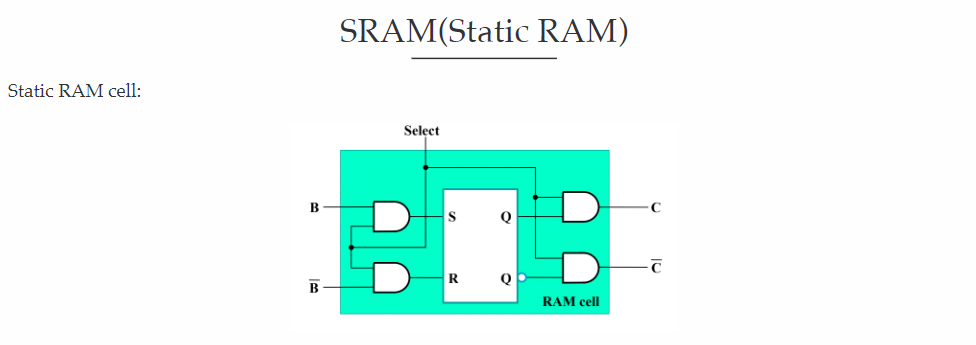
- SRAM的单元是由flip-flop构成的，每个单元需要6个transistor。因此SRAM的面积比DRAM大，但是速度快，不需要refresh。 - Logic diagram如下：

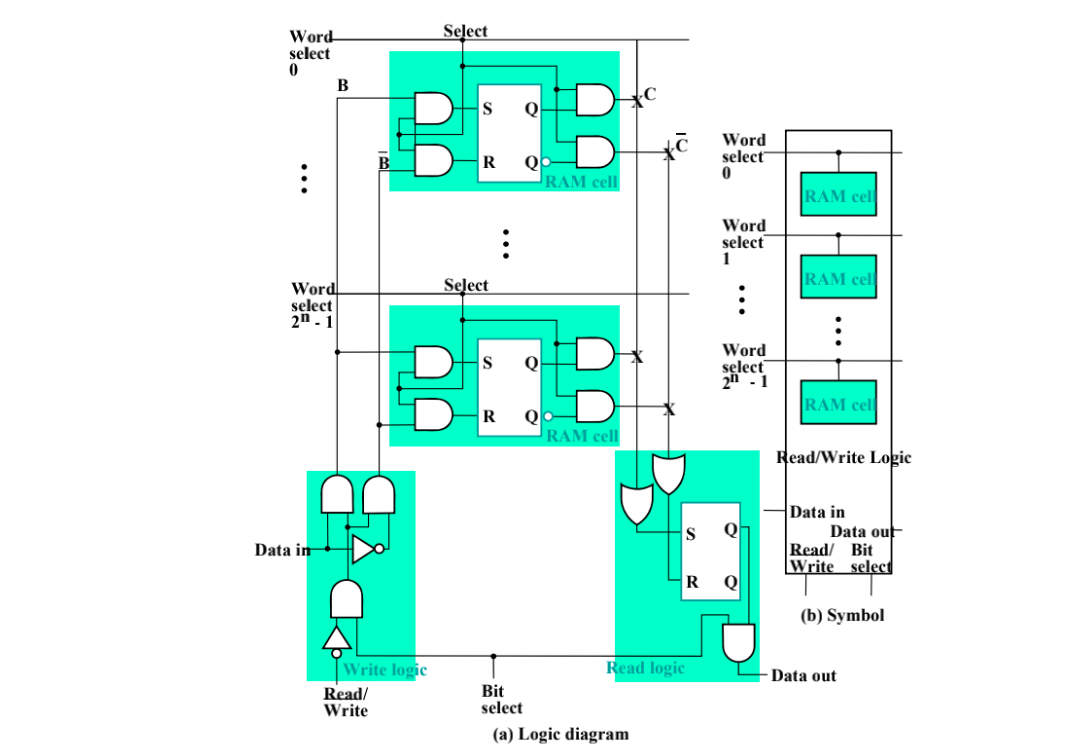
Operations

The two operations that a random-access memory can perform are write and read.

The process of storing new information in memory is referred to as a memory write operation.
The process of transferring the stored information out of memory is referred to as a memory read operation.

Namely, A write is a transfer into memory of a new word to be stored. A read is a transfer of a copy of a stored word out of memory.

Write

The steps that must be taken for a write are as follows:

Apply the binary address of the desired word to the address lines.
Apply the data bits that must be stored in memory to the data input lines.
Activate the Write input.

The memory unit will then take the bits from the data input lines and store them in the word specified by the address lines.

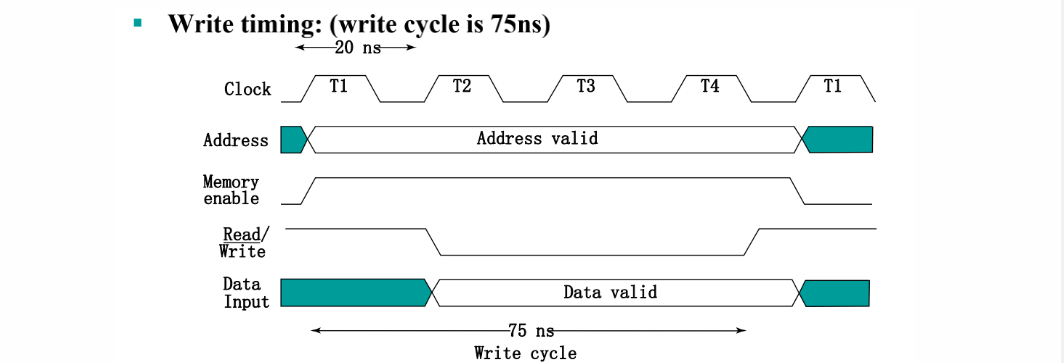
write

白色有效，绿色无效。高电平读，低电平写。

Write: - 将有效的地址放到address input lines上。将写入的数据放到data input lines上。 - 激活写入控制。

Data⼀定要在0-1前保持⼀段时间来建⽴并且0-1后维持⼀段时间才能正确写⼊。

最后提前变读，以防止错误写入

Read

The steps that must be taken for a read are as follows:

Apply the binary address of the desired word to the address lines.
Activate the Read input.

The memory will then take the bits from the word that has been selected by the address and apply them to the data output lines.

The contents of the selected word are not changed by reading them.

read

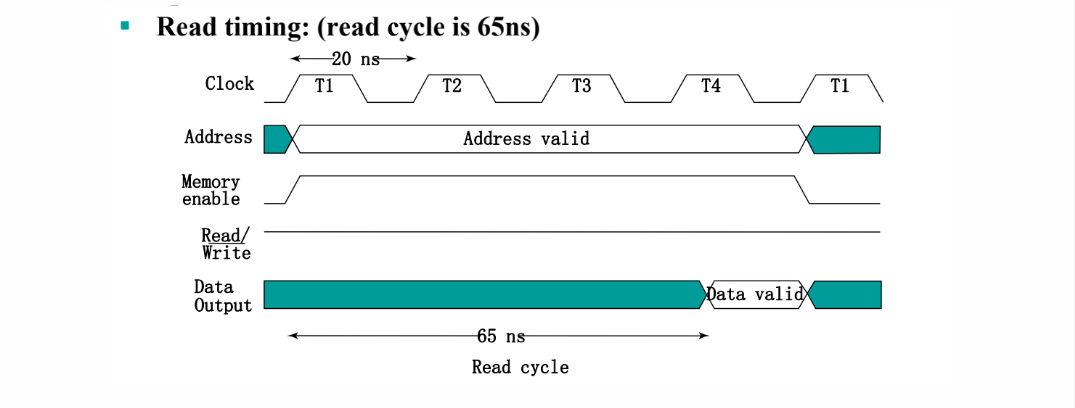
白色有效，绿色无效。高电平读，低电平写。

Read: - 将有效的地址放到address input lines上。 - 将read control line置为1。 - 等待读出的数据稳定，将数据从memory output lines读出。

一般读比写快。

Word

A word is an entity of bits that moves in and out of memory as a unit—a group of 1s and 0s that represents a number, an instruction, one or more alphanumeric characters, or other binary-coded information.

A group of eight bits is called a byte.

Most computer memories use words that are multiples of eight bits in length. Thus, a 16-bit word contains two bytes, and a 32-bit word is made up of four bytes.

The capacity of a memory unit is usually stated as the total number of bytes that it can store.

Communication

Communication between a memory and its environment is achieved through data input and output lines, address selection lines, and control lines that specify the direction of transfer of information.

A word in memory is selected by its binary address. When a word is read or written, the memory operates on all 16 bits as a single unit.

The 1K * 16 memory of the figure has 10 bits in the address and 16 bits in each word. The number of address bits needed in memory is dependent on the total number of words that can be stored and is independent of the number of bits in each word.

The number of bits in the address for a word is determined from the relationship $2^k >= m$, where m is the total number of words and k is the minimum number of address bits satisfying the relationship.

Size

Computer memory varies greatly in size. It is customary to refer to the number of words (or bytes) in memory with one of the letters K (kilo), M (mega), or G (giga). K is equal to 2^10, M to 2^20, and G to 2^30.

eg

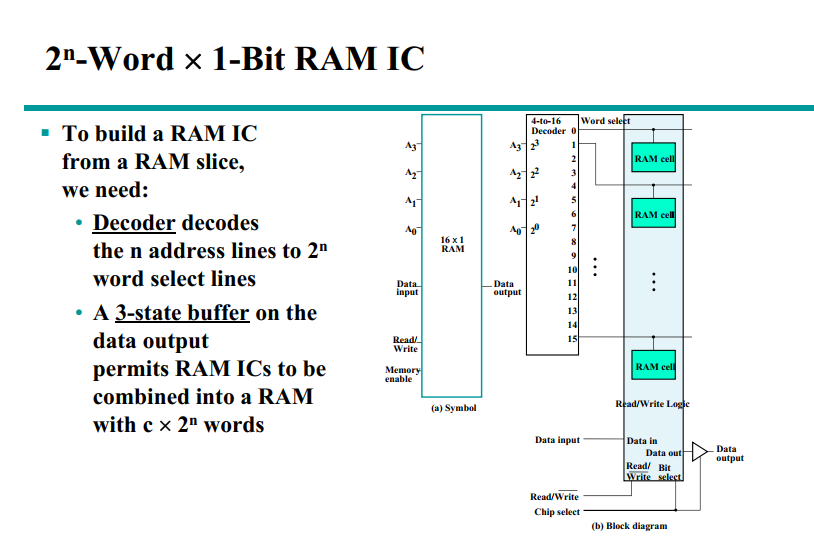
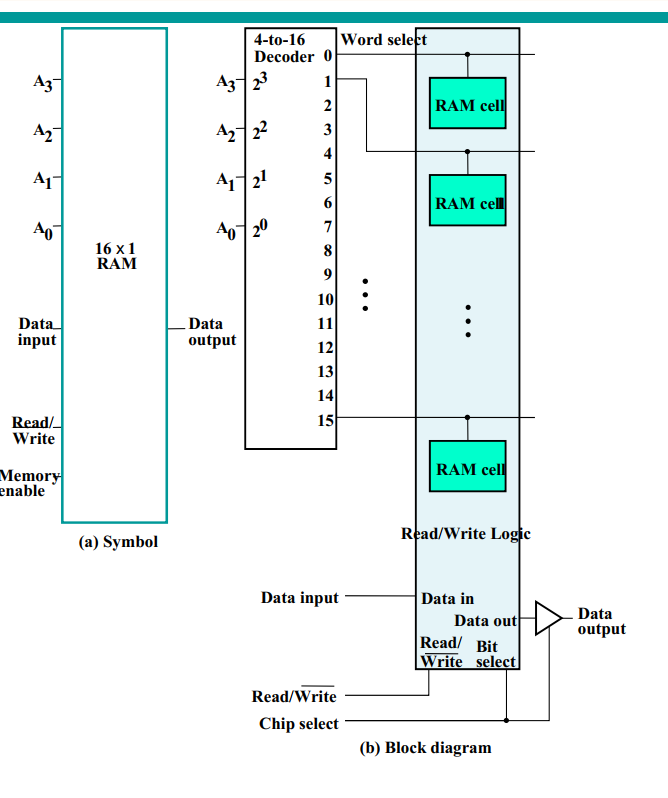
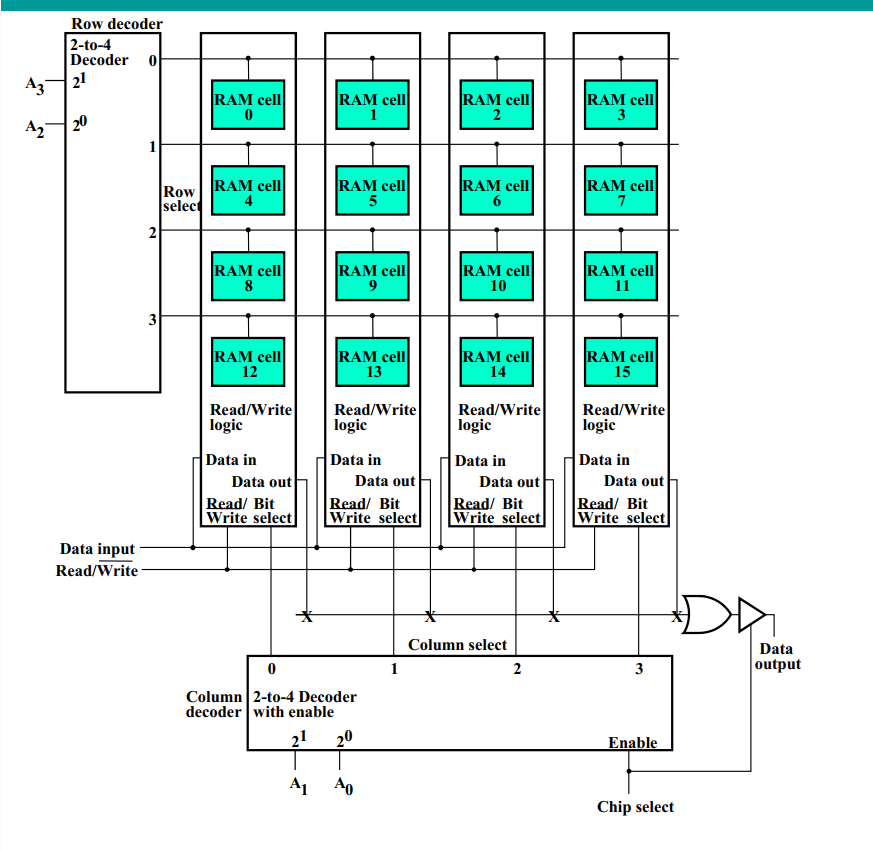
横坐标和纵坐标分开译码

译码器成本降低，速度更快