7-AA2
Greedy Algorithms
给定一个目标函数/优化函数(optimization function),取值有限制(constraints),限制下的子空间叫 feasible solutions,我们希望在限制下求一组使得函数值最大化/最小化的最优解(optimal solution)
简单来说,就是,面对规模为N的子问题,我们类似分治拆分为子问题,一般是让每个 stage 的规模减少1,然后让N-1的最优解加上按某策略得到的元素,就是N得最优解
比如,我们要从北门去南门,我们贪心策略就是就每到一个路口就往南走
Activity Selection Problem
Huffman Codes – for file compression
NP-Completeness
Approximation
Approximation Ratio 近似比就是近似解与正解之间的比值取大于1的比值的上界
\(\rho (n)\) 即近似比,其值为规模 \(n\) 时能得到的最大比值
近似比越小,精确度越高,算法也越慢越麻烦
a value \(\epsilon\) > 0 such that for any fixed \(\epsilon\), the scheme is a (1+ \(\epsilon\))-approximation algorithm.
如果算法的复杂度与\(\epsilon\)有关系就是一个PTAS
既与\(\epsilon\)有关系还与规模有关系就是 fully polynomial-time approximation scheme (FPTAS)
Approximate Bin Packing
- Next Fit 近似比为2, 关键点是两个相邻的箱子物品体积和 \(> 1\)
- First Fit 每次决策就依次检查前面所有的箱子,能放就放,都不行才开新箱子
- Best Fit 在First Fit基础上,优先选前面剩余体积最多的箱子放
上面三个算法很垃圾,是顺序决策,只考虑过去,没考虑未来
我们称这种一个输入即时进行决策的算法叫在线算法,且决策是不能更改的,用于不知道输入是什么情况的情景
任何在线算法我们都能设计出一组解,让近似比大于5/3
离线算法就是完成所有输入后,才开始决策
The Knapsack Problem — fractional version
背包问题,我们放的东西不仅仅有体积,还有价格,而且还可以切开,切开后价格有系数 \(p_i\) 进行修正,使切后总价减少,我们希望让背包价格最大
正解算法是,找出性价比最高的物品,能整个放进去就放,不能就切了放进去,然后循环,保证性价比高的东西先进去
这个问题有一个变种叫0-1版本,即物品不能切了,要么放要么不放
The K-center Problem
Local Search
Randomized Algorithms
Parallel Algorithms
Parallel Random Access Machine (PRAM)
Work-Depth (WD) Presentation
评价并行算法需要考虑两个因素
- Work load: total number of operations W(n)
- Worst-case running time: T(n)
由这两个因素我们得出以下的指标:
-
W(n) operations and T(n) time
- T时间里完成的W工作量
-
P(n) = W(n)/T(n) processors and T(n) time
- T时间、P处理器数量
- on a PRAM,不能用于WD模型
-
W(n)/p time using any number of p ≤ W(n)/T(n) processors
- 这个算法能支持W(n)/T(n)个处理器,但是手上没这么多处理器,只有p个
- on a PRAM,不能用于WD模型
-
W(n)/p + T(n) time using any number of p processors
- 分情况
- 如果p很大,那么这个式子就是T(n),表示算法支持的最大处理器数量下的耗时
- r如果p很小,那就是W(n)/p,同第三个
- on a PRAM,不能用于WD模型
- 分情况
后面三个只能用于PRAM,因为PRAM将所有处理器平等对待的,工作量相等的,而WD模型会根据处理器情况,让好的多干点
Partitioning
External Sorting
优化问题
pass的数目有:
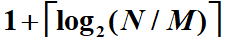
对于k路合并,我们一共需要2k个tape,因为从tape的角度来看,k路合并就是k个tape用于输入,k个tape用于输出,然后反复交换身份
满足斐波拉契数列的分法是不需要copy的,是最完美的,其它情况无论如何都得copy
对于k路,就是k阶的斐波拉契数列
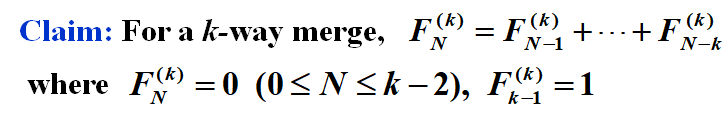
现在我们k路归并只需要k+1个tape了
内存问题
内存得单独拿一个作为 output buffer

实际情况是,tape上的两个block被输入给input buffers,并在这里对record进行排序,输出给output buffer,但是output buffer会小很多,所以会反复满,反复输出给tape
我们再加一个output buffer,两个output buffer轮流工作,就能保证CPU并行进行排序和I/O不间断
输入也可能导致CPU空闲,即一个input buffer空了的时候,又得通过I/O写进新的block,,我们可以给每个input tape多配一个input buffer
综上,对于k路合并,我们需要2k个input buffer和2个output buffer
动态run:
最小化归并时间
run需要反复归并,我们尝试用哈夫曼树找出最优解

归并的时间与被归并的record数量成正比
这里的操作次数可以看成 \(2+4 +6+5+11+15=43\)