1_AVL&SPLAY
:material-circle-edit-outline: 约 359 个字 :material-clock-time-two-outline: 预计阅读时间 1 分钟
AVL
Define

Height

Trouble Finder

Splay 树
Splay 树,即伸展树,想要解决的问题和 AVL 树类似,只不过 Splay 树希望达到的目标是在摊还(Amortized)复杂度 \(O(logN)\) 的情况下完成大部分对点操作。
为使 AVL 保持平衡,我们需要维护从根节点到 Trouble Maker 这条路径上所有点的平衡因子。而 Splay 则不再维护这些信息,这意味着我们无法保证 Splay 树的状态都是平衡的,但是我们希望它尽可能平衡。
对于一个树,我们对其节点进行的操作可能是:增点、删点、改点、查点等等,而不同类型的操作开销可能不尽相同。
摊还分析
分析对象
开始分析之前,我们首先需要明确分析的目标:
对于 Splay,它不存在明显的减势和增势行为,所有我们提到的操作都依赖于将目标点旋转到根来实现,而这也成为其主要开销。
部分常数操作显然被覆盖,插入之类的操作之所以能被忽略的原因,可以参考 ltgg 的这篇文章)
其中我们会用到若干次 zig、zig-zag、zig-zig 的操作。

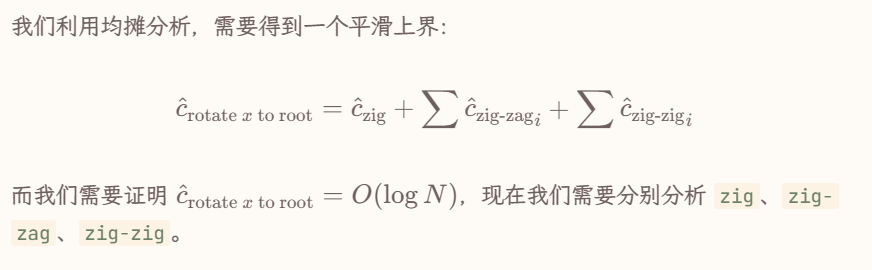
势能函数

我们定义一棵二叉树的秩为从为从根节点开始到其叶节点中最长的一条树链上结点的个数。
