Skip to content

REVIEW 4 | Leftist Heap & Skew Heap

:material-circle-edit-outline: 约 1338 个字 :fontawesome-solid-code: 95 行代码 :material-clock-time-two-outline: 预计阅读时间 6 分钟

Leftist Heap

左偏树（又称左倾堆）是通过结构上的不平衡实现效率上的提升。相比于普通的堆，支持快速的堆合并操作。

概念

“左偏”，不断将新的东西往右侧合并，并不断维护使得左边比右边大，来实现每次都是往相对小的那一侧塞进东西

我们每次操作后都会进行维护，让左偏性质始终成立，这样每次右侧都是相对小的

由于左偏堆不再是一个完全二叉树，所以我们不能再像维护大根堆小跟堆那样用数组来维护它了。

一个左偏堆的结点维护了左右子堆的地址、自身的键值、和一个“npl”。

image-20240319112603331

struct LeftistHeapNode {
    ElementType val;
    int npl;
    LeftistHeapNode * ls, * rs;
};

npl

The null path length, Npl(X), of any node X is the length of the shortest path from X to a node without two children.

有两个孩子的结点是内部节点，否则是外结点。

npl就是某节点到任一外部节点的最短路径

外部节点npl为0，内部节点的npl为1

叶子结点是度为0的结点，也叫终端结点

Define Npl(NULL) = –1.

计算npl类似往下数有向边，null是方向反过来往上找到自己的父结点，所以为-1

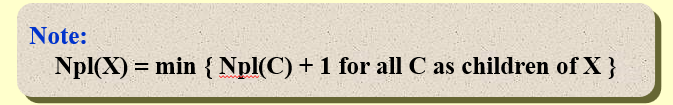
image-20240319104410208

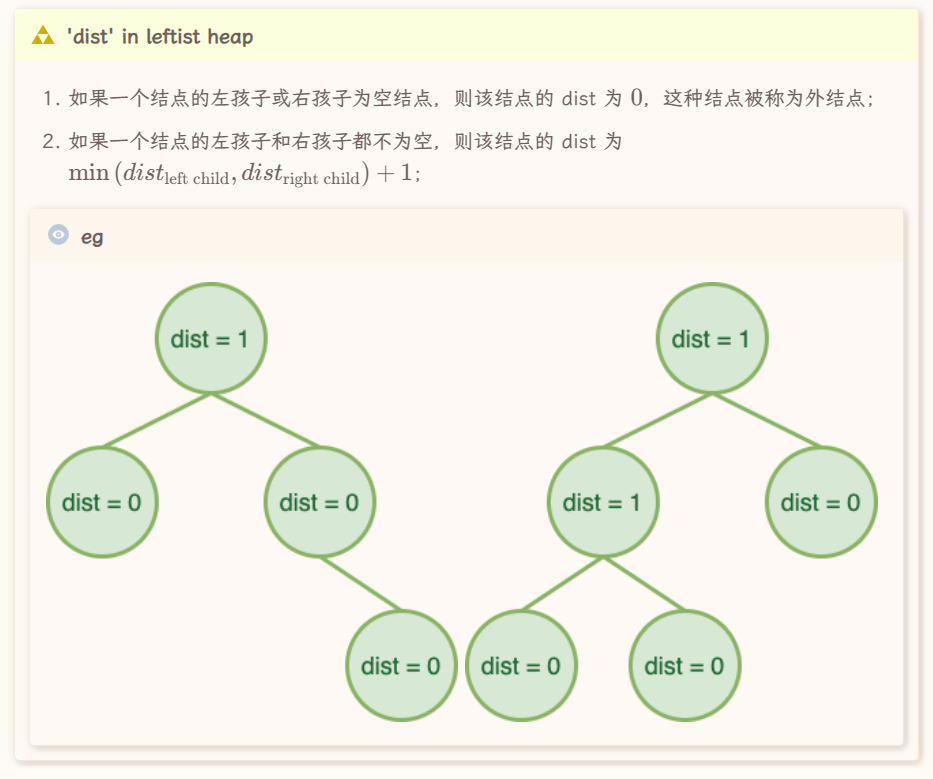
image-20240401113443320

性质

左偏堆结点的键值应当不大于（不小于）其孩子结点的键值的二叉树（即堆的性质），

且满足「左偏」性质——结点的左孩子的 npl \(\geq\) 右孩子的 npl。

我们可以得到扩展性质：

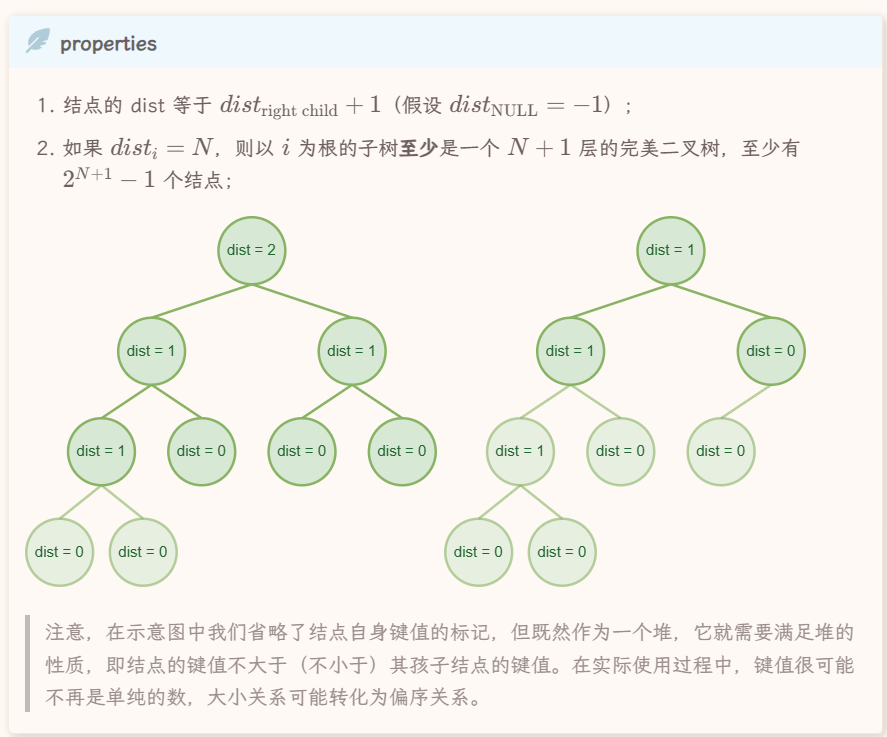
image-20240401113658972

右路径

从root出发，一直往右，走到没有右儿子为止的这条路径，即整棵树最右边的边

image-20240319105453137

即由右路径长度推出树的结点数的下限

image-20240319111438698

就上面的定理反过来，推右路径上限

这个结论告诉我们，右路径的结点不会很长，所以我们可以决定让所有的操作都只对右路径的结点进行，这样就能保障低时间复杂度

操作

左偏堆的核心操作就是合并，其它操作都可以看作是合并的特殊情况。

合并

注意是都在右路径操作，插入就放在最右下角

大致思路就是先维护堆的性质，在回溯时维护左偏性质，所以实际上它是一个先自上而下再自下而上的过程。

左偏堆的合并可以分为递归式和迭代式两种。前者可能更为直觉，后者可视化后则更为直观。

递归式

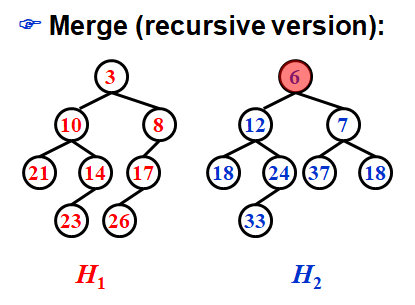
image-20240319114017655

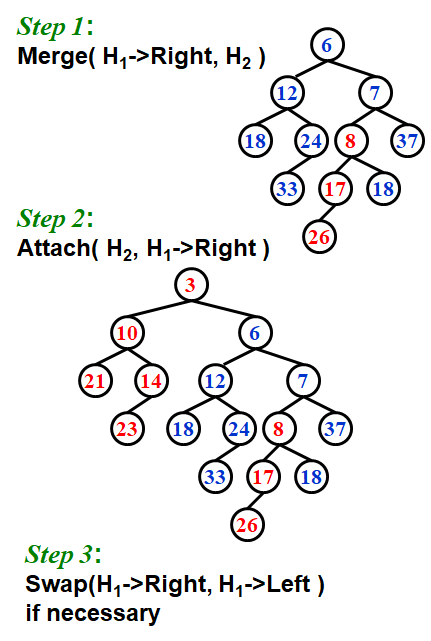
image-20240319114041540

step 1是因为只对右路径进行操作，所以排除左子树，迭代为对H1的 root 右子树和H2进行合并。至于谁是H1，看谁的root最小

Step 3是因为结果右子树npl比左大，而堆不要求左右子树有次序关系，所以可以直接交换左右子树

共迭代右路径长度的次数

image-20240319115113928

image-20240319115729281

LeftistHeapNode * merge(LeftistHeapNode * x, LeftistHeapNode * y) {
    // Recursive exit. If any is NULL, return the other as the new root of subtree.
    if (x == NULL) return y;
    if (y == NULL) return x;

    // If `x`'s val is smaller than `y`'s, swap them, which means we always operates on `x`.
    if (x->val > y->val) {
        swap(x, y);
    }

    // Merge `x`'s right subtree and `y`, and set `x`'s right subtree to the result.
    x->rs = merge(x->rs, y);

    // If `x`'s left subtree's dist is smaller than `x`'s right subtree's dist, swap them.
    if (x->ls->dist == NULL || x->ls->dist < x->rs->dist) {
        swap(x->ls, x->rs);
    }

    // Update x's dist.
    x->dist = x->rs->dist + 1;

    // Return x as the new root of subtree.
    return x;
}

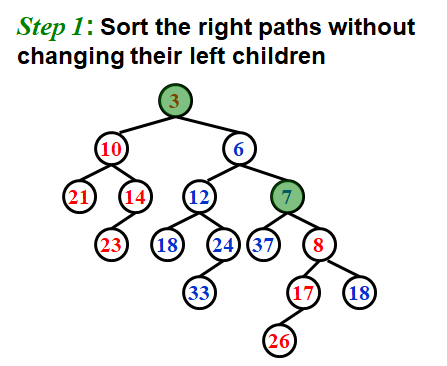
迭代式

因为我们不对左子树进行操作，所以我们可以分离出每棵树的左子树+根节点作为一个样本，子树同理，然后对这些样本进行最小堆的合并操作

image-20240319121222243

LeftistHeapNode * merge(LeftistHeapNode * x, LeftistHeapNode * y) {
    // `tx` & `ty` are the pointers to the roots of the subtrees that haven't been merged.
    LeftistHeapNode * tx = x, * ty = y;
    // `res` is the root of the merged final tree, while `cur` is the latest node that has been merged.
    LeftistHeapNode * res = NULL, * cur = NULL;

    // Begin merging.
    whie (tx != NULL && ty != NULL) {
        // If `tx`'s val is smaller than `ty`'s, swap them, which means we always operates on `tx`.
        if (tx->val > ty->val) {
            swap(tx, ty);
        }

        // Specially mark the root on the first merge.
        if (res == NULL) {
            res = tx;
            cur = tx;
        } else {
            cur->rs = tx;
            cur = cur->rs;
        }

        // Go on.
        tx = tx->rs;
    }

    // Merge the rest of the tree.
    while (ty != NULL) {
        // Specially mark the root on the first merge. (rarely happens but not impossible)
        if (res == NULL) {
            res = ty;
            cur = ty;
        } else {
            cur->rs = ty;
            cur = cur->rs;
        }

        // Go on.
        ty = ty->rs;
    }

    // Adjust the left and right subtrees of all the nodes according to the properties of `dist`. 
    // It does the same work as the adjust part in the recursive version. I ignore it here.
    res = adjust(res);

    return res;
}

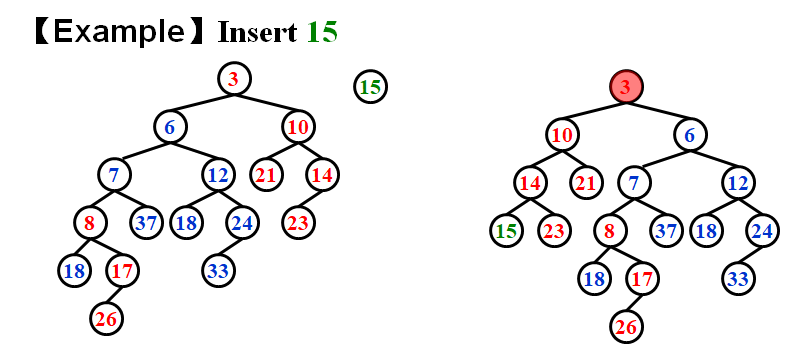
单点插入

插入结点可以看作合并一个只有一个结点的左偏堆，所以我们可以直接复用合并过程。

单点删除

让我们一般性地考虑一个结点，与它相关的主要有三个方向：父结点和两个孩子结点。

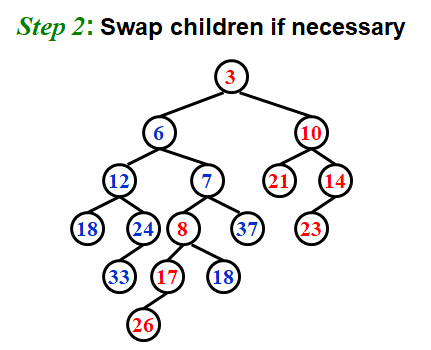
而单点删除的操作也很简单，只需要合并需要被删除的结点的两个子结点，然后将这个新的树的根代替被删除的结点，再在回溯的过程中 bottom-up 地更新 dist 即可。

删除根节点，合并两颗左偏树

image-20240319121747526

我们发现只有右路径上的结点会出错，所以依次检查右路径结点的npl，依次进行交换

image-20240319121308834

LeftistHeapNode * del(LeftistHeapNode * cur, ElementType x) {
    if (cur->val == x) {
        // Just return the merge of the children.
        return merge(cur->l, cur->r);
    } else {
        // Not this subtree.
        if (cur->val > x) return cur;

        // Otherwise, search the `x`.
        if (cur->l != NULL) del(cur->l, x);
        if (cur->r != NULL) del(cur->r, x);

        // Adjust the dist bottom-up.
        adjust(cur);
    }
}

Skew Heap

斜堆(Skew Heap)是比左偏堆更为一般的数据结构，它同样有着能够快速合并的性质。

左偏堆需要自下而上地维护 npl，所以我们无法进行并发操作。

AVL 树同样为了维护平衡性质无法进行并发操作，而红黑树则通过一个能够仅仅通过变色就能调整的黑高来规避了必须自下而上维护的问题，实现了并发。

换句话来说，要想将左偏堆改变地能够进行自上而下维护，就需要改变甚至放弃它的左偏性质的严格性——而这就是斜堆的由来。

斜堆也需要满足大根堆（小根堆）的性质，而它的合并和左偏堆的合并也十分类似，只不过我们这次无条件的交换左右子树。

斜堆就是不管如何，先交换再说。

换句话来说，不管左偏性质如何变化，我们都会选择交换参与合并的左右子树。

No Npl.

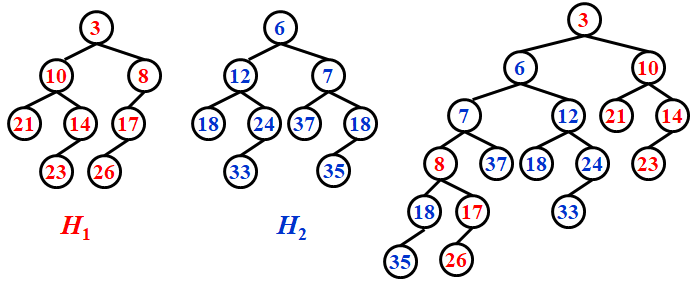
合并

反正都要交换，我们放样本的同时直接将其左子树放到右子树的位置

image-20240319125348335

插入

image-20240319125537383

Amortized Analysis for Skew Heaps

右子树结点比左子树多就是重结点，反之为轻结点