Skip to content

REVIEW 5 | Binomial Queue

:material-circle-edit-outline: 约 777 个字 :material-clock-time-two-outline: 预计阅读时间 3 分钟

Priority Queue

优先队列不是按照顺序出来，而是按照优先级，比如最大的/最小的。

堆的其中一个应用就是优先队列。

Binomial Queue

概念

二项队列是一个二项树的集合（森林），且每一个高度的二项树最多只能有一个

二项树

  • 二项树定义

    • 高度为0的二项树只有一个结点。
    • 高度为k的二项树由两个k-1的合成

  • 二项树性质

    • 二项树带有堆的顺序性质（任意子树最大/最小key在根节点）。
    • k 阶二项树都是同构的，且 k 阶二项树是两个 k−1 阶二项树合并得到的。
      • 其合并方式是两颗树比根节点大小，大的直接称为 小的 的孩子
      • 这也决定了二项树的根每一个 child 本身也都是一个二项树。

数量性质

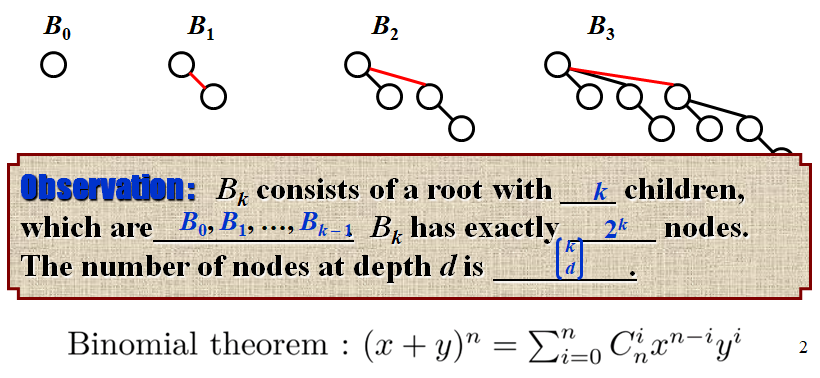
image-20240327090022378

k是高度，一个节点高度为0

二项队列与二进制

任意大小的二项队列都是唯一确定的

  • 在一个二项队列这个森林里，每一高度的树要不没有，要不只有一颗（有两颗必须合并）。
    • 所以任意高度的树只有0个1两种情况
    • 所以可以用二进制表示二项队列，类比二进制加法进行合并运算
  • 二项树的总结点数正好满足\(2^k\)的规律
    • bin对应的dec即二项队列的总节点数

操作

FindMin

image-20240327083908357

最小堆顺序的情况下，每颗二项树的minKey都是root，只需要比较logN个根节点即可

优化：储存最小的根节点，每次有改变都进行检测与更新

Merge

两个二项队列合并很确定，直接二进制树加法；三个就会有不确定的地方，先是哪两个合并？

对于FindMin，合并哪两个无所谓，因为最小的一定还是根

合并方式是两颗树比根节点大小，大的直接称为 小的 的孩子

Insert

实际上就是merge从1开始

image-20240405170053147

DeleteMin

delete的套路就是转化为merge

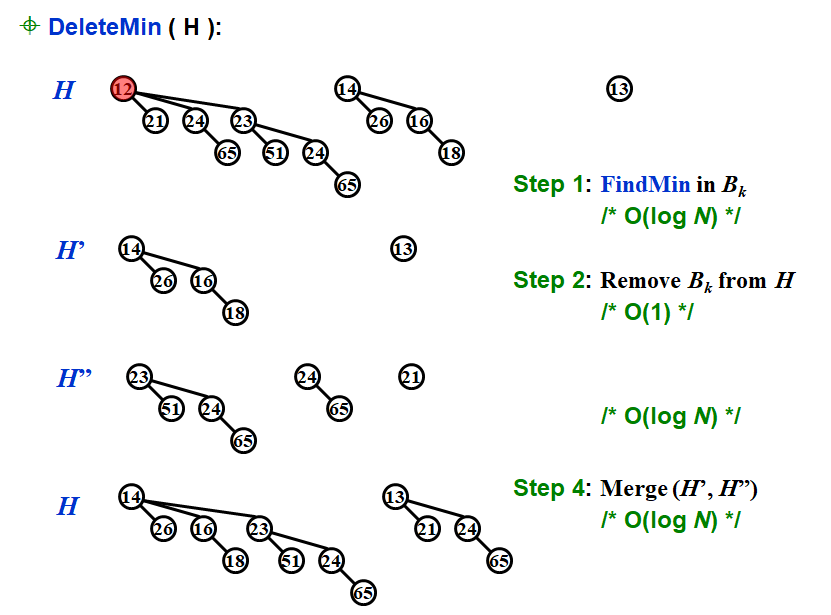
image-20240327090214714

删除最小的根，将这个根下的子树当成新的二项队列，与原来的剩下的队列进行合并

H’’ 需要被放到一个新的数组，即遍历每一个root，所以复杂度是logN

Implementation

二项树的实现

二项树没有随机访问儿子的需求

  • 左儿子右兄弟
    • 每个node依旧两个指针，一个指向原来最左边的儿子，一个指向兄弟

合并的两棵树是一样大的。如果兄弟是递增顺序的话，因为被合并的是最大的树，导致要前往放其的位置需要遍历到最后面

但是递减的话就能很快了

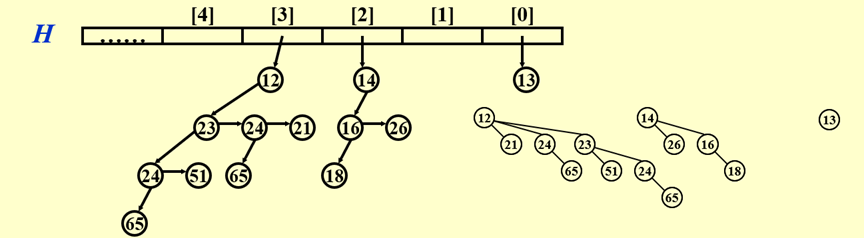
image-20240327092050933

总结一下刚刚的两个点：形式与顺序

image-20240327091717063

代码

数据结构

image-20240327092200788

MergeTree

image-20240327092536571

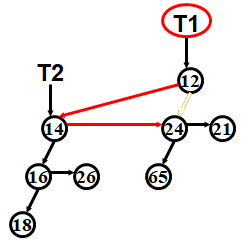
image-20240327092550913

MergeQuene

image-20240327092937596

从低位往高位遍历合并，不懂就类比二进制加法

DeleteMin

包含四个步骤

image-20240327094105085

均摊分析

这里没看