PTA习题回顾
HW1 AVL & SPLAY & AMORTIZED ANALYSIS
Fill-in-Blank - P - ZJUADS_杨洋2024_HW1 (pintia.cn)



B 应该是 minimum。


HW2 RBT &
NULL结点不是叶子节点,叶子节点必须有key
这里的“叶子结点”被重新定义了,为了描述方便,现在称所有两个子结点都是 NIL 的结点为末端结点(也就是通俗意义上的叶子结点)。
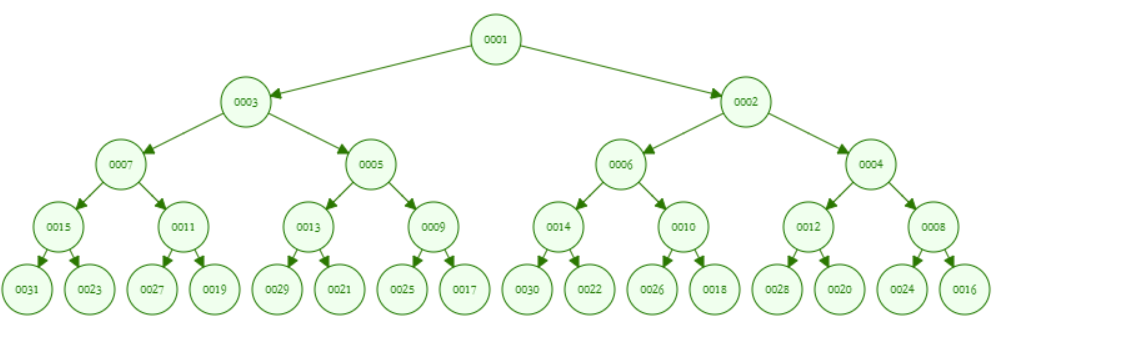
下图的红黑树是否合法?
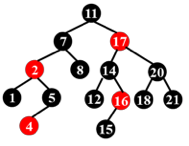
不合法。
16号节点的右儿子是一个黑叶子,而这个叶子到根的路径上只有 3 个黑节点,而其他叶子到根都有 4 个黑节点。所以我们需要警惕只有一个非叶儿子的红色节点。
我们得到这样一个结论:
合法红黑树不存在只有一个非叶子节点的红色节点!
or
合法红黑树的红色节点的两个子节点一定都是叶子或都不是叶子!

这题做一下,熟练插入操作

这题做一下,熟练删除操作
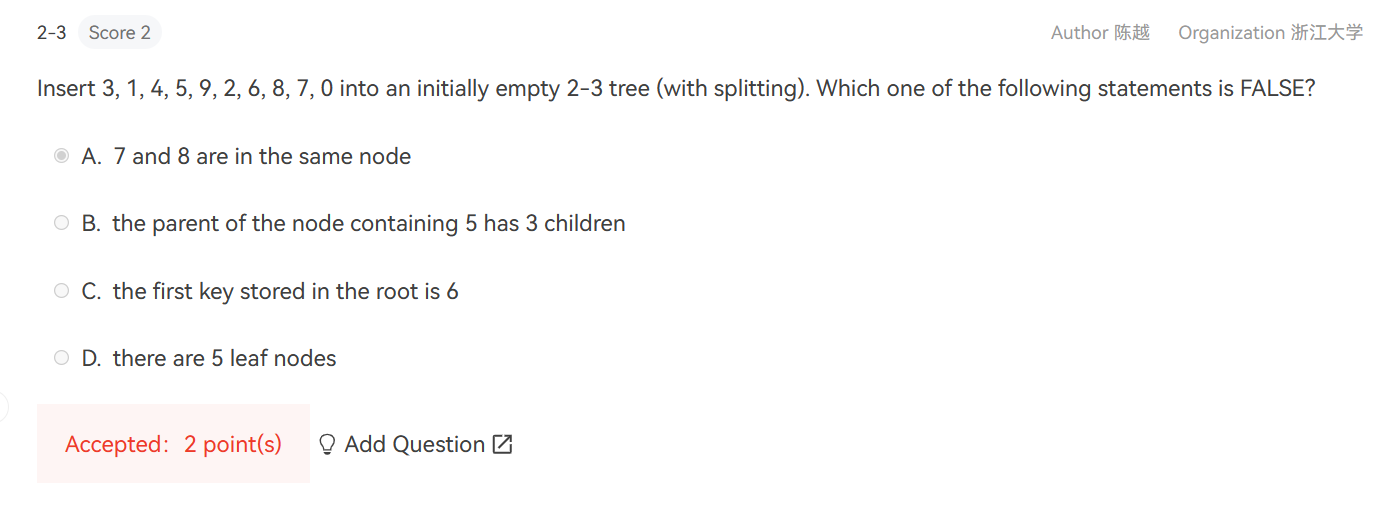
ADS的定义由不同,需要重做!!!!
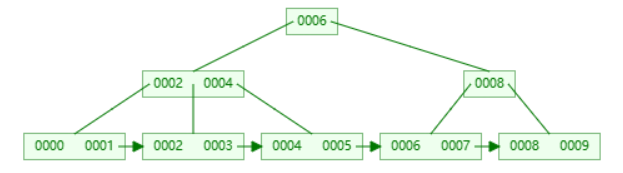

这题还没做
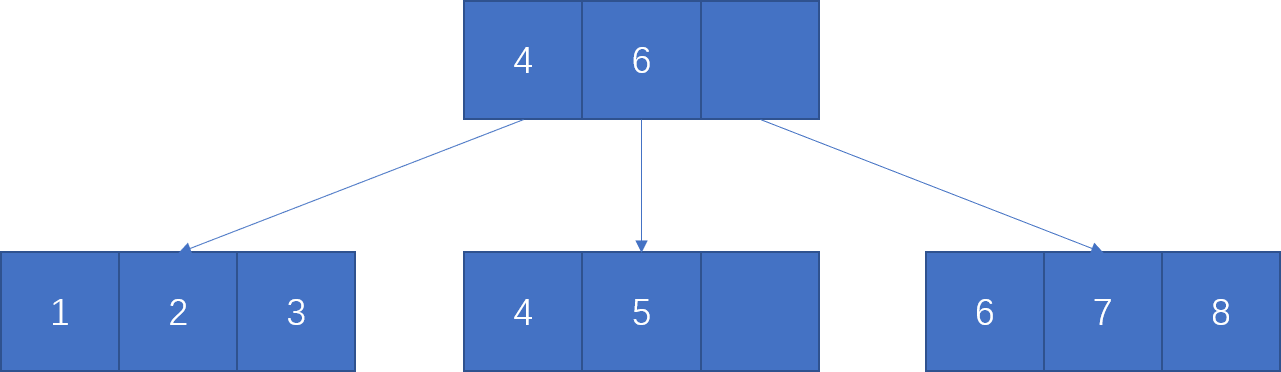

HW3
哈希/散列插入删除O(1),二叉树为O(logn)
这个是term-partitioned策略
document-partitioned是根据每个文档的唯一标识符或其术语子集将其分配给节点

data retrieval:数据检索/召回
relevancy:相关性
召回率和整个答案集的相关性无关。

安全至上,尽量都发现。
召回率指的是检测到所有爆炸物的比例。即使只有一次漏检,也可能造成灾难性后果。 因此,即使部分检测结果为误报 (即查准率较低),也必须确保尽可能检测出所有可能的爆炸物 (即高召回率)。

Benchmark set,基准数据集或测试集,用于评估算法或模型性能的数据集,通常包含一系列精心挑选的样本,具有代表性且难度适中,能够反映算法或模型在实际应用中的表现。
查准率高但召回率低,意味着系统倾向于返回非常相关的答案,但可能会遗漏一些同样相关的答案。
特征 索引(index) 搜索 定义 一种用于快速查找信息的数据结构 一种用于查找满足特定条件的信息的过程 目的 提高信息检索的速度 查找所需的信息 工作方式 使用键值对来组织信息 在信息集合中遍历数据 应用 数据库、文件系统、搜索引擎等 各种应用场景,包括网络搜索、桌面搜索等
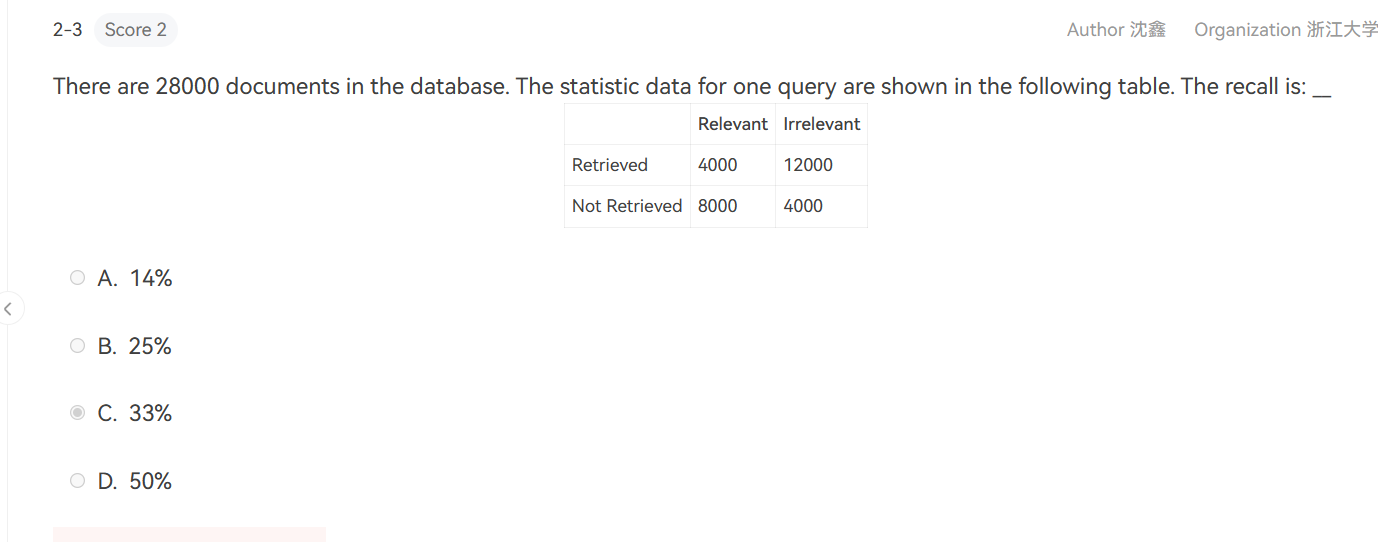
recall=4000/(4000+8000)=33%
不相关的不用管
HW4
注意合并是将子树拆离出来与待合并树合并,合并完了再接回去。
不一定是待合并树插入这个子树,也可以是这个子树插入待合并树。

注意插入是怎么插入的,自己用笔画一下
skew heap 只有轻结点受类似 leftist heap 的限制。
相对而言,leftist heap 就不能这么任意了,它受 logN 限制。
leftist heap 的右路径长度需要整体结点数量的支撑
\(l_r=n\rightarrow N_{min} = 2^n-1\)

递归法
左偏堆先不要管左偏性质,在右路径上找到插入位置,然后将这个位置下面的结点及其子树拆离,接上待插入树;被拆离的子树作为新的待插入树,递归
插入结束后,往回递归检查,即从下往上看左偏性质是否被破坏,破坏了就左右交换,直至根节点
迭代法
也是先不要管左偏性质,在右路径上找到插入位置。
但是迭代法需要将两棵树都拆成一个个样本,然后对这些样本按照根节点大小顺序进行合并
注意,左子树里面的右子树不要拆,左子树是一个整体
个人习惯
上面两个实际用草稿纸画的话很相似,都差不多
代码就不知道了
某一结点下面接一个三角形,表示其子树与原题一致,未变化

C是对的,故最差应该是O(N)

注意斜堆每次插入完,都要在右路径上从下往上,每层交换,直至根节点
顺序插入自己找规律,很好找
先右路径,从大子树到小子树
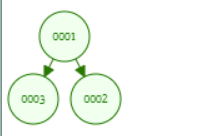
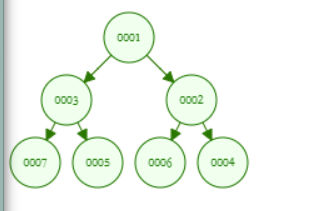


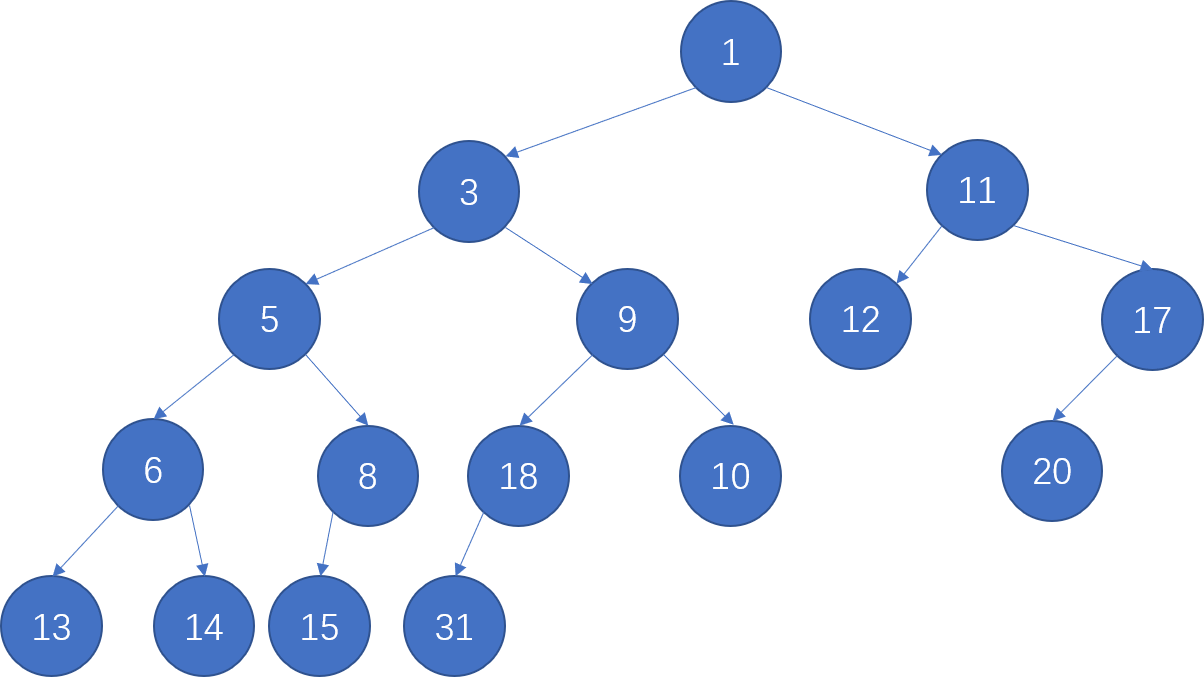
斜堆合并用迭代法不对劲,重新试试
用递归法是正常的,子树合并后接回去
这题没必要画出合并后的树
左子树不会变,每层都交换;交换后的子树化为整体,即不会再变化

HW5


均摊都常数时间了,平均肯定是常数时间。
????????
find-max 比较难操作,find-min 也是常数时间。
merge 和 delete-min 都是 O(logN)。


>=
T->NextSibling != NULL