Lecture 2 势能法与红黑树
参见2025王道数据结构P299
势能法
势能法还不懂
定义算法中的某个指标或其映射为势能,跟踪运算过程中这个指标的变化,将相邻操作的势能差作为credit
要选好的势能函数,一般变化小的好点。没有什么套路,只能多看多练
例如mutipop栈的元素数量作为势能

90min:去看算法导论上的例子
下面是势能法常用不等式,证明想看就看

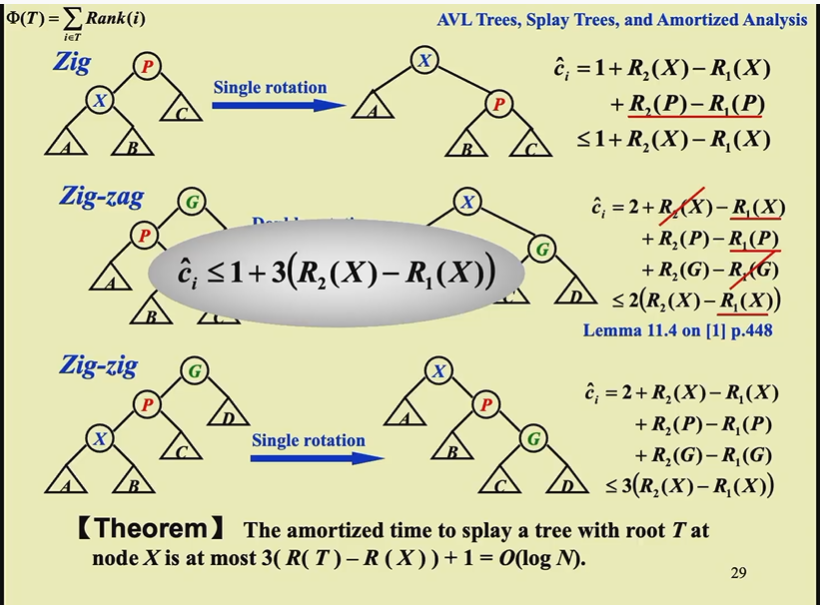
分析splay tree
红黑树
代码小技巧
让每个leaf指向一个值特殊的虚拟节点,方便访问左儿子和右二子,就不用每次访问儿子都需要if是不是null。这个虚拟节点被叫做 哨兵/外部节点。
即,让叶子节点的空儿子从指向null改成指向哨兵。
红黑树在AVL的基础上放宽
每个节点多一个颜色属性
性质
五条性质(要背下来,按顺序背,方便听课用)
- 每个节点要么红,要么黑
- 根节点黑
- 叶子节点黑,即哨兵是黑
- 红节点儿子全黑
- For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.
- 是到哨兵,不是到叶子节点
- 插入红的不影响性质五
黑高,即从该节点到哨兵的黑色节点数,不算自己和哨兵

如上:11的黑高是1,8的黑高是0,4的黑高是0
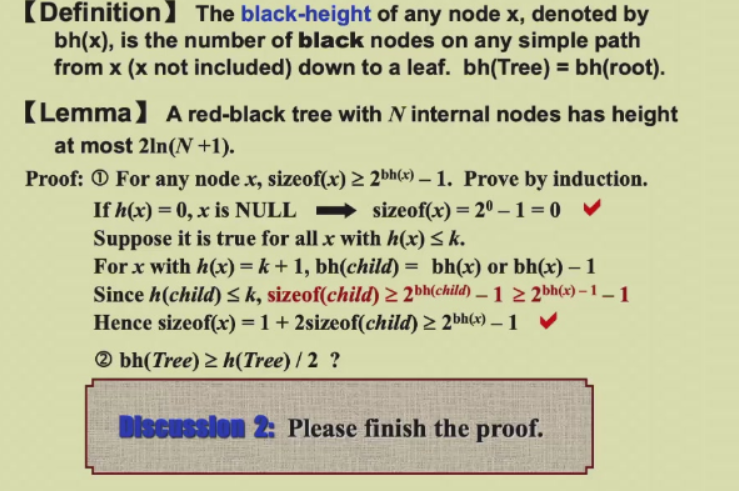
黑高定理

数据结构讲课套路
性质:顺序性质,结构性质
操作:比如查询,插入,删除
复杂度等特殊性质
操作
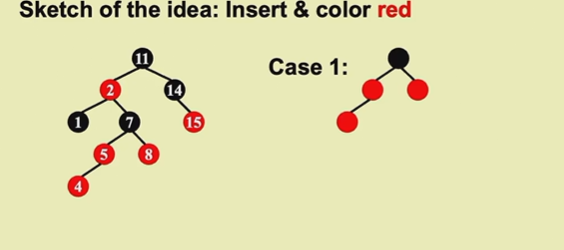
insert
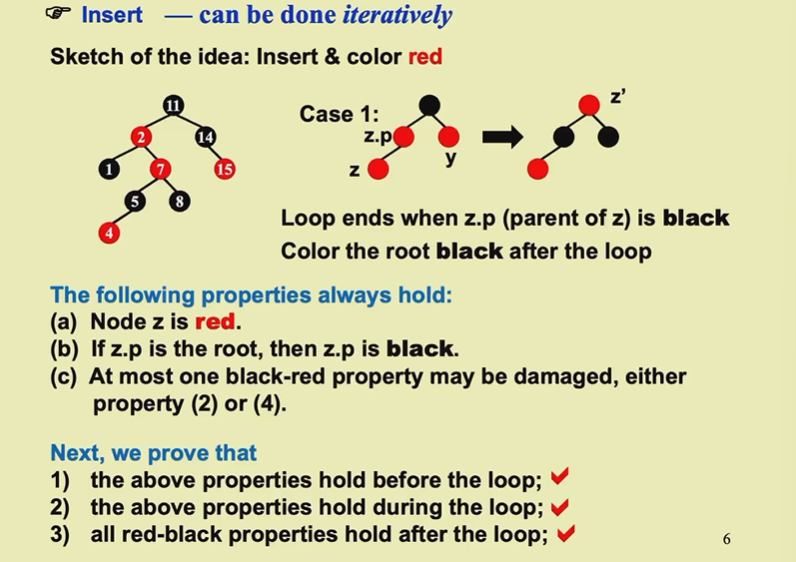
插入都初始化为红色,可能破坏二、四,一三五都不会影响
而且子树内的变化会影响外部
那我们就试着从下开始调整,往上甩锅,从而往上递归解决,根不动即可
分三情况解决,可以覆盖所有情况
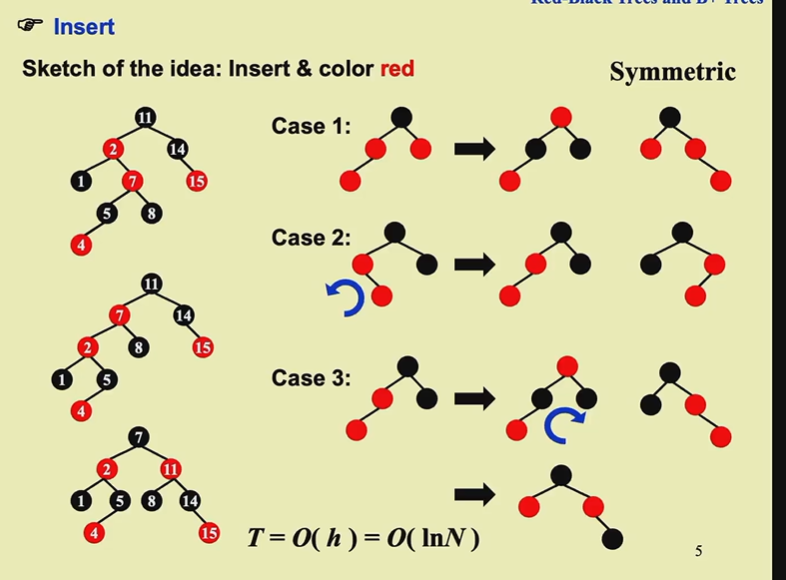
关键看叔叔,叔叔是红就爷爷背锅,是黑就看是近还是远;近叔叔就旋转变为远叔叔,然后就给父亲染黑,然后旋转父亲
case1
违背了性质四,则将父节点的黑色传给两个儿子节点,并把这个父节点染红,从而恢复性质四且保证这个子树内性质五成立。
但是又根据性质四,原本为黑色的父节点的父节点上面可能是红色节点,这样改变后可能这两个节点又违反性质四。我们往上递归就好。
case2
出现左右儿子一红一黑情况,无法让父节点的黑色传下来。直接让红色儿子变黑会导致黑高不平衡。为了解决这个问题,我们先不染色,而是让两个相邻的红色节点先做一次旋转,进入case3.
至于为什么要旋转,是因为如果不转到左边,case3旋转时下面的节点会被分配到右边,进而会违背性质四
case3
直接改变一个红色儿子会导致黑高不平衡,这个时候应该想到AVL树,AVL树的旋转就是为了解决不平衡的问题。于是这里先染色,然后做一次旋转,就平衡了。
证明思路
算法导论有这些case操作的严格证明
整个过程中有三点是一直成立的
Delete
怎么转化?????
删除非叶子节点实际上可以转化为删叶子,所以我们只讨论删叶子节点
删红的随便删
删黑的肯定会违背性质五,其它不违背
得分五种情况
delete很多地方和insert是对称的
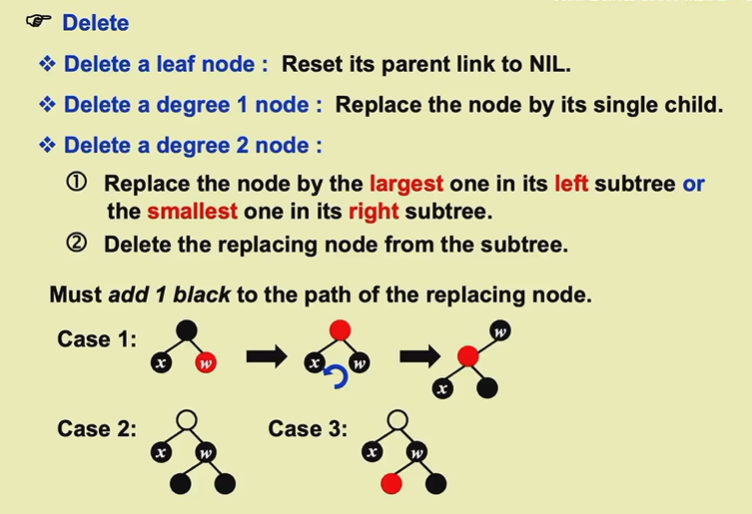
先让要被删除的节点x变成很黑(+1),然后开始以下case
case1
case1核心想法就是将自己的一份黑色往上传,为保持性质五就让兄弟也往上传一份黑色。
如果兄弟是红色,我们就先旋转,让一定是黑色的侄子变成我们的兄弟,就可以一直往上传黑色了。
但是如果兄弟是黑色的,侄子可能是红色,这里得分情况讨论。
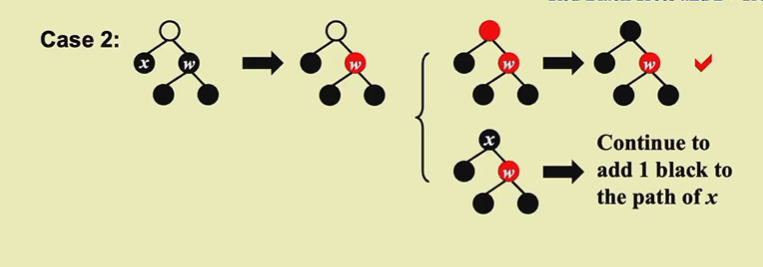
case2
承接case1,如果侄子都是黑色的,完美。
- 如果父亲原本是红的,那么就完事了
- 如果父亲原本是黑色,就得继续往上传
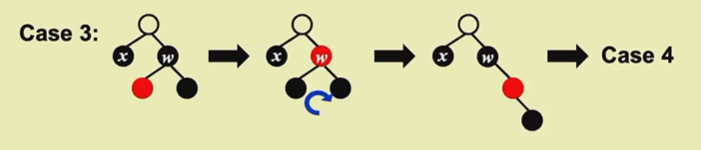
case3
承接case1,如果侄子一红一黑,又得分情况,关键看远侄子
远侄子是黑的,那么近侄子是红的。先让兄弟和红侄子颜色互换,此时黑高左高,那么就右转一下。这下就有红的远侄子了,进入case4.
case4
这部分最难最复杂
承接case3。此时我很黑,兄弟是黑的,远侄子是红的。
先把父亲和兄弟颜色互换,然后把远侄子染黑,然后提起兄弟(左旋),完事。
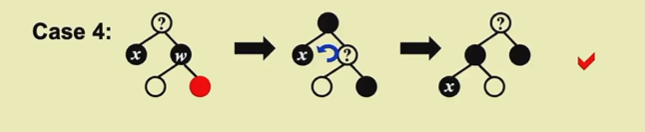
此时可以删掉x了。
上面的操作是让x所在的子树黑色多点,因为x被删之后需要有人承担他的黑色
课后过一下slide的删除例子90min
作业
RBT操作比较复杂,情况多,难记忆,多做题
图库上传失败

2-2一定要重做,没搞懂循环指向哪
