Lecture 4
Leftist Heaps
左偏树(又称左倾堆)是通过结构上的不平衡实现效率上的提升
npl
有两个孩子的结点是内部节点,否则是外结点。
npl就是某节点到任一外部节点的最短路径
外部节点npl为0,的npl为1
叶子结点是度为0的结点,也叫终端结点
The null path length, Npl(X), of any node X is the length of the shortest path from X to a node without two children.
Define Npl(NULL) = –1.
npl数目类似数有向边,null是反过来往上所以为-1
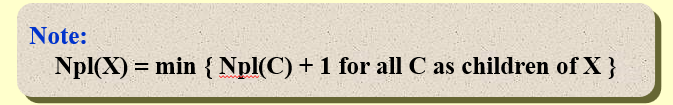
property
左偏树就是任一结点左儿子nul不小于右儿子npl,即左右相等或左大。
The leftist heap property is that for every node X in the heap, the null path length of the left child is at least as large as that of the right child.

右路径是指从root出发,一直往右,走到没有右儿子为止的这条路径
用数学归纳法证明,注意数学归纳法假设是假设小于等于k的时候成立,不是等于k的时候成立

这个结论告诉我们,右路径的结点不会很长,所以我们可以决定让所有的操作都只对右路径的结点进行,这样就能保障低时间复杂度
define

merge
合并的前提:都在右路径上操作
recursive version
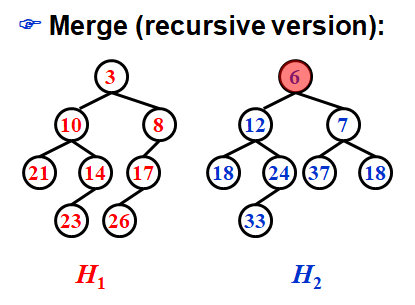
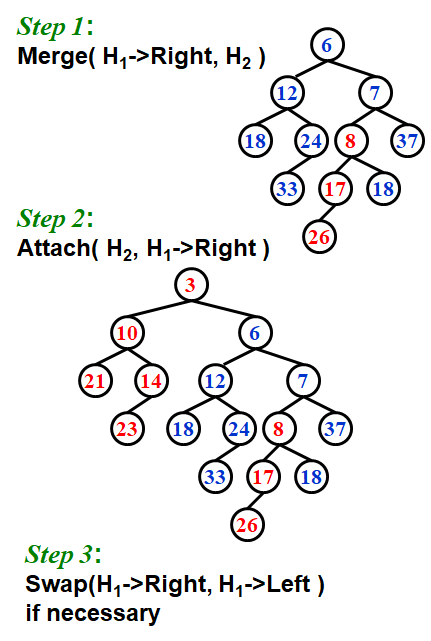
step 1是因为只对右路径进行操作,所以排除左子树,迭代为对H1的root右子树和H2进行合并。至于谁是H1,看谁的root最小
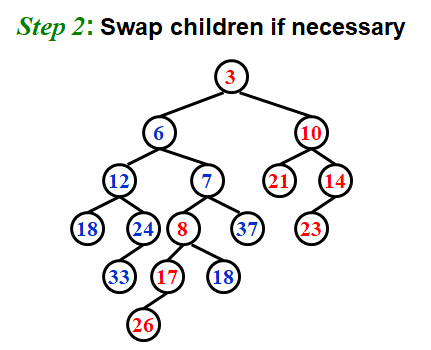
Step 3是因为结果右子树npl比左大,而堆不要求左右子树有次序关系,所以可以直接交换左右子树


共迭代右路径长度的次数
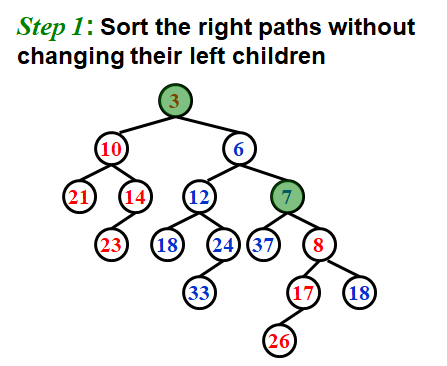
iterative version
因为我们不对左子树进行操作,所以我们可以分离出每棵树的左子树+根节点作为一个样本,子树同理,然后对这些样本进行最小堆的合并操作
delete
删除根节点,合并两颗左偏树

我们发现只有右路径上的结点会出错,所以依次检查右路径结点的npl,依次进行交换
OI Wiki
什么是左偏树
是一种 可并堆,具有堆的性质,并且可以快速合并
dist 的定义和性质
和上面的npl类似,
Skew Heaps
斜堆之于左偏树就像splay之于AVL,目标是不要求每次合并都是logN,而是要求从空树开始所有操作均摊上限为logN
左偏树中每次merge一个结点和都需要检查其左右儿子,计算npl,然后判断是否要进行交换。
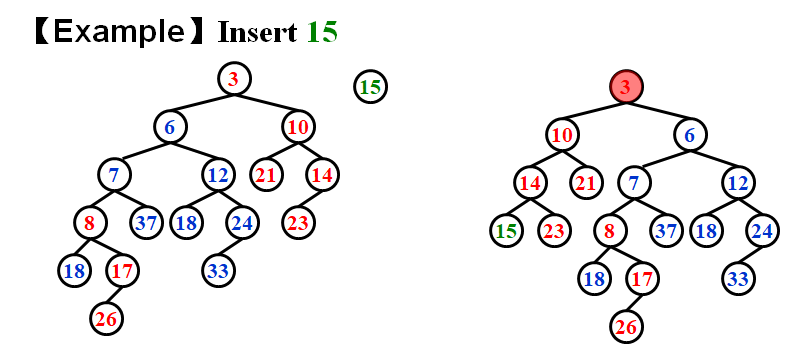
斜堆就是不管如何,先交换再说。
好的,斜堆讲完了。
斜堆merge代码就是把左偏树中关于npl计算、判断和交换的代码去掉就是了。
很神奇。
Always swap the left and right children except that the largest of all the nodes on the right paths does not have its children swapped.
No Npl.
反正都要交换,我们放样本的同时直接将其左子树放到右子树的位置
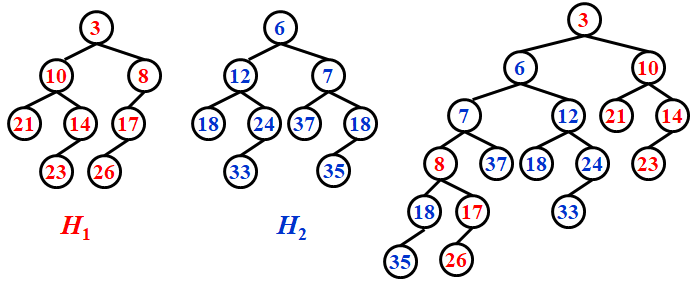

斜堆worse bound更差,但均摊一样,在超大项目中节省了很多算力和空间。
Amortized Analysis for Skew Heaps
常用势能法
数据结构中常用的势能函数是其规模,例如结点个数
势能函数只有一个要求:最初值为最小值
但是在这里以及之前的splay不用结点个数是因为在merge操作里这个函数都是在增长
而好的势能函数需要相对均衡的有起有伏
我们用重结点的个数作为势能函数
【Definition】A node p is heavy if the number of descendants of p’s right subtree is at least half of the number of descendants of p, and light otherwise.
Note that the number of descendants of a node includes the node itself.
即右子树结点比左子树多就是重结点,反之为轻结点