Lecture 7|Divide and Conquer
:material-circle-edit-outline: 约 506 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟
分治法
什么是分治法
递归地分解问题为子问题,递归地解决子子问题,递归地合并问题

T(N)为解决规模为N的问题的开销
分为了a个子问题,每个子问题规模为N/b
合并的开销为f(N)
渐进上界
关键在于
f(N),下面给出f(N)=N和f(N)=N^2的例子
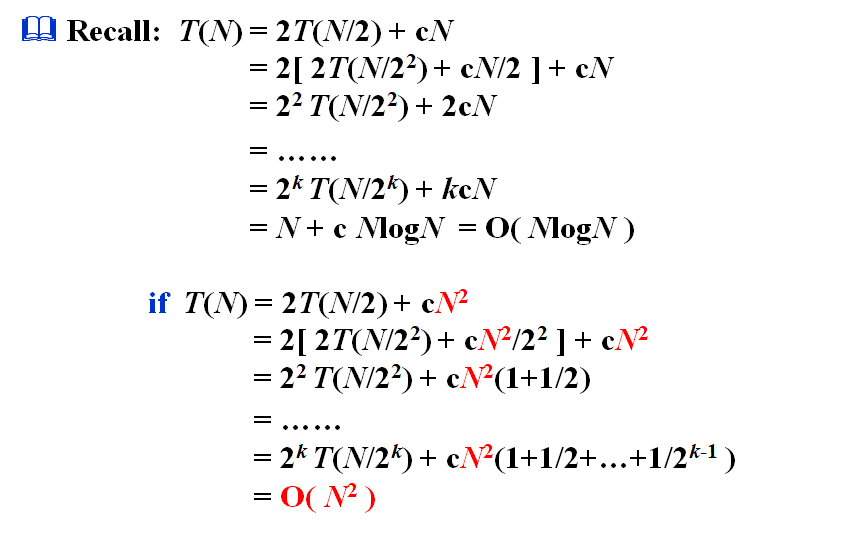
Closest Points Problem
平面上有N个点,请找出直线距离最小的两个点
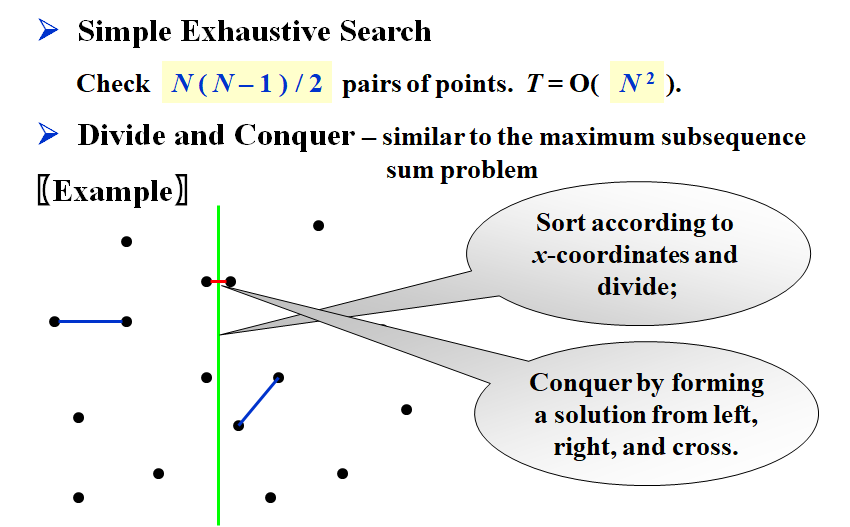
简单地分治会错过红线情况,而这恰恰是正解
于是我们在子问题中加入检测不同子问题里面的点集合间的情况
但是直接检测本质上和遍历没区别,我们就进行剪枝
例如先找到子问题里的最优解,然后检测每一个点到分界线的垂直距离,如果这都比最优解长,以后都不用考虑这个点了
\(\delta\) 是目前两个子问题的最优解

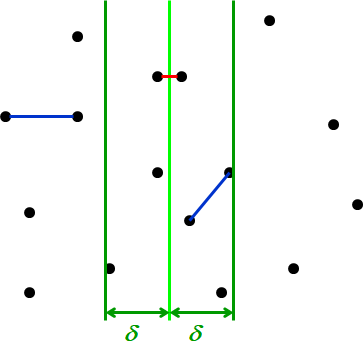
进一步优化,不仅考虑横轴,还考虑纵轴距离范围,对于纳入考虑的点,看下与另一点的纵向距离是否大于\(\delta\)
而且只需要从上往下即可,因为上面的矩阵里的点已经被测试过了
就是矩阵高是\(\delta\)而不是\(2\delta\),测试中的点在左上角的顶点而非中线处

课后实现一下这个算法,比较困难
技巧是维护两个队列
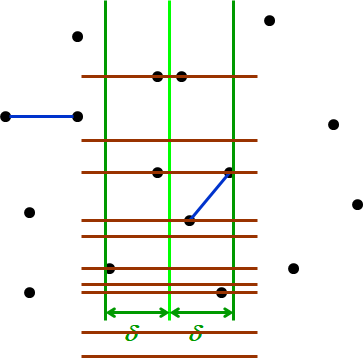
这样只需要检测一个个矩阵里的点即可
下面是最坏情况,即矩阵里点最多的情况

中间黑白的意思是两个点重叠在一起
Methods for solving recurrences
需要重看PPT

代入法
瞎猜法
猜出上界,归纳法证明
技巧:


这里意思是不能从\(T<cN+N\)证明出\(T<cN\),,前者更松,后者更紧
递归树法
边画边猜法

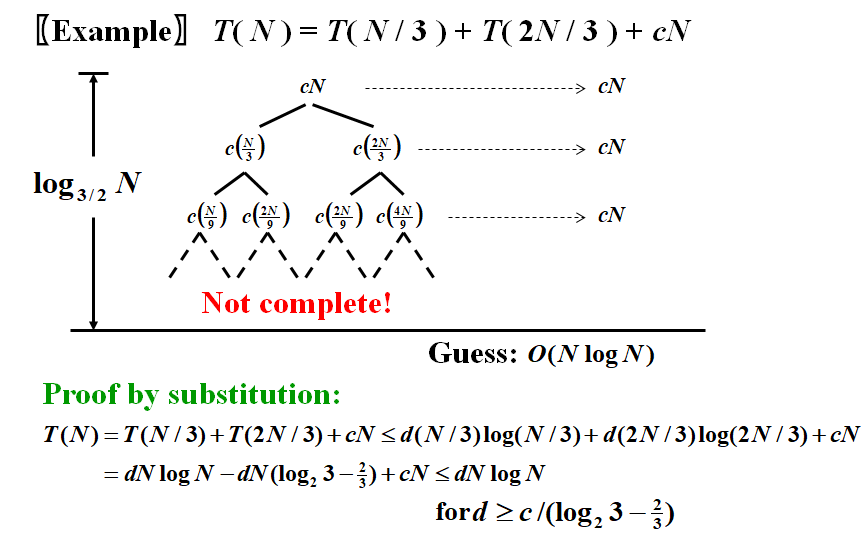
主方法
求偶法

第一个就是叶子特别多时,就只看叶子
第 个是根特别大,就只看根