Lecture 8 Dynamic Programming

:material-circle-edit-outline: 约 713 个字 :fontawesome-solid-code: 26 行代码 :material-clock-time-two-outline: 预计阅读时间 3 分钟

算过的东西如果会重复利用就先保存到表里，要用时直接从表里取

DP的代码比较简单，考试经常考

这节课全是例子

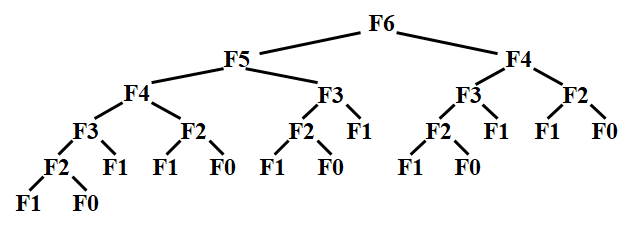
引入--斐波那契数列

对于斐波拉契数列，我们可以得到 F(N) = F(N – 1) + F(N – 2) ，这个递推式在动态规划里叫状态转移方程，用于描述子问题与较大子问题之间的转移关系

状态用于描述子问题

int  Fib( int N ) 
{ 
    if ( N <= 1 ) 
        return  1; 
    else 
        return  Fib( N - 1 ) + Fib( N - 2 ); 
}

改进后：

int  Fibonacci ( int N ) 
{   int  i, Last, NextToLast, Answer; 
    if ( N <= 1 )  return  1; 
    Last = NextToLast = 1;    /* F(0) = F(1) = 1 */
    for ( i = 2; i <= N; i++ ) { 
        Answer = Last + NextToLast;   /* F(i) = F(i-1) + F(i-2) */
        NextToLast = Last; Last = Answer;  /* update F(i-1) and F(i-2) */
    }  /* end-for */
    return  Answer; 
}

例1--矩阵乘法

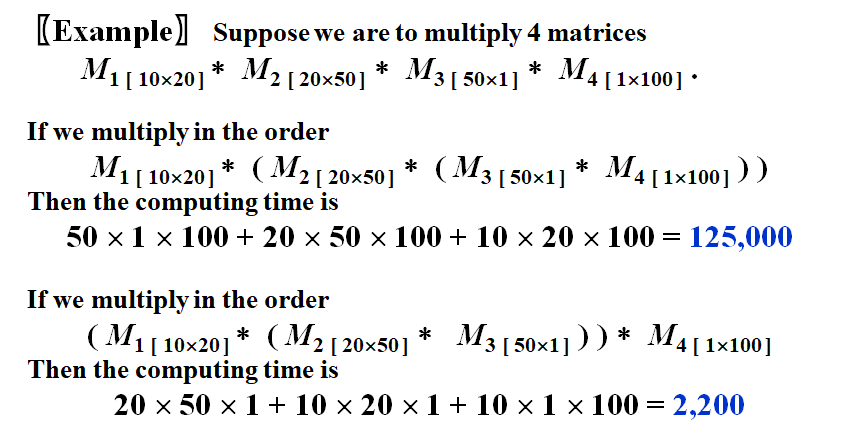
上面的式子看懂就行，就是多个矩阵相乘，顺序不同会导致开销也不同

我们想知道开销最小的顺序

可以先试试枚举法

我们先看下n个矩阵相乘有多少种相乘情况，这可以用DM解决 ↓

tip：如果你不知道怎么设计状态转移方程，可以想一下最后一步会怎么做

在这里的最后一步就是，最后是哪两个矩阵相乘？最后一定是左边一堆矩阵乘出来的矩阵 \(M_{1,i}\)，与右边一堆矩阵乘出来的矩阵\(M_{i+1,n}\)，这两个矩阵相乘。只是我们不知道他们的分隔点 \(i\) 在哪

这样，我们就将 \(M_n\) 拆分为了两个子问题，当然注意要枚举，因为 \(i\) 是变量

DM中枚举经常出现，当然是枚举情况

上面那个公式不要管，记得是指数增长就行

公式下面是开销问题的DM解法

注意到，这个问题中，第k个问题的最优解依赖于第k-1个元素的最优解，这个条件叫做最优子结构

最优子结构性质是状态转移方程成立的两大条件之一

How to design a DP method?

1. Characterize an optimal solution
2. Recursively define the optimal values
3. Compute the values in some order
4. Reconstruct the solving strategy

最重要就是设计状态，不知道怎么设就先设F(N)

Optimal Binary Search Tree

让总检索期望最少

整体上让概率大的靠近root，小的靠近leaf

（就是哈夫曼树）

从子树累计可得到状态转移方程

得检查是否满足最优子结构

状态转移方程第二个必要性质：重叠子问题，即不同状态调用同一个子问题状态，是否还指向同一个解

替换，把子问题最优解替换进去看下是否变差

All-Pairs Shortest Path

完全不懂

拿跳板数量作为状态

这就是Floy算法

Product Assembly

有一堆汽车零件加工为汽车，t是时间开销，我们想找一条最小时间开销的流水线

高级数据结构与算法分析2024-05-13第3-5节 (zju.edu.cn)

自己写一次状态转移方程

f[0][0]=0;  f[1][0]=0;
for (stage=1; stage<=n; stage++){
    for (line=0; line<=1; line++){
    f[line][stage] = min(
        f[  line][stage-1] + t_process[  line][stage-1],
    }
}
Solution = min(f[0][n],f[1][n]);

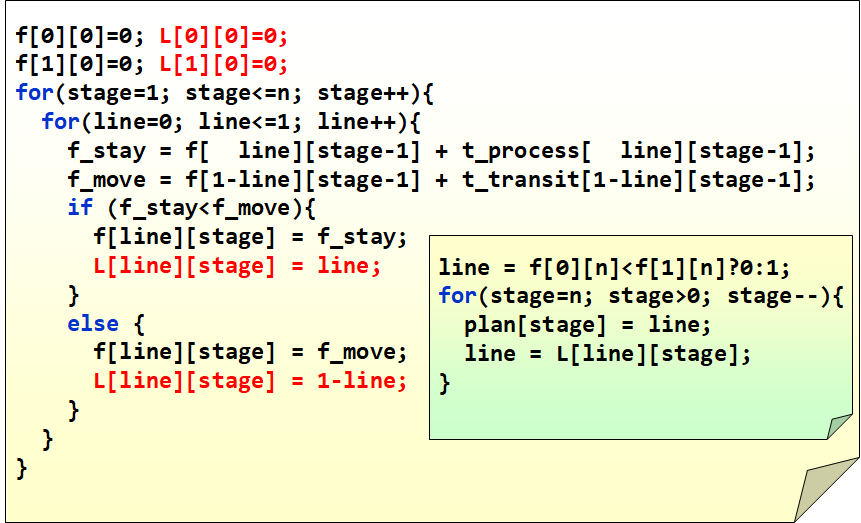
LCS