Lecture 11 | Approximation
对于无法得到解的问题,我们可以找近似解。
近似算法一般用来解决优化问题,毕竟判定性问题二选一没啥意思
但是不能胡乱猜,所以我们引入近似比用来衡量近似解。
Approximation Ratio
就是近似解与正解之间的比值

\(\rho (n)\) 即近似比,其值为规模 \(n\) 时能得到的最大比值,显然一定大于1
如果一个近似算法得到的解与正解比值 \(\leq \rho(n)\),我们就说这是一个近似比为 \(\rho(n)\) 的近似算法
近似比越小,精确度越高,算法也越慢越麻烦
设计近似算法时,需求一般会给一个近似比作为设计的限制条件
【Definition】 An approximation scheme for an optimization problem is an approximation algorithm that takes as input not only an instance of the problem, but also a value \(\epsilon\) > 0 such that for any fixed \(\epsilon\), the scheme is a (1+ \(\epsilon\))-approximation algorithm.
We say that an approximation scheme is a polynomial-time approximation scheme (PTAS) if for any fixed \(\epsilon\) > 0, the scheme runs in time polynomial in the size n of its input instance.
即,如果算法的复杂度与\(\epsilon\)有关系就是一个PTAS
既与\(\epsilon\)有关系还与规模有关系就是 fully polynomial-time approximation scheme (FPTAS)
Approximate Bin Packing
给N个体积不同的物品,要将他们放进体积固定的箱子,希望找出箱子最少的答案。这是一个NPC问题。
检查这个问题解是不是最优解,可以物品总体积除箱子得到下界,拿来大概比较一下,当然这样还不够hhh
对于这个问题我们有三个算法:
解法
Next Fit
简单粗暴,物品一个一个检查,能放就放进去,放不下就开新箱子,当前箱子就不管了
这是一个近似算法,反例就是0.3,0.8重复出现
void NextFit ( )
{ read item1;
while ( read item2 ) {
if ( item2 can be packed in the same bin as item1 )
place item2 in the bin;
else
create a new bin for item2;
item1 = item2;
} /* end-while */
}
【Theorem】 Let M be the optimal number of bins required to pack a list I of items. Then next fit never uses more than 2M – 1 bins. There exist sequences such that next fit uses 2M – 1 bins.
即近似比为2
下面证明近似比哪来的

关键点是两个相邻的箱子物品体积和 \(> 1\)
First Fit
上个算法明显的问题就是每次决策只考虑了上个箱子的信息,信息太少
那我们每次决策就依次检查前面所有的箱子,能放就放,都不行才开新箱子
void FirstFit ( )
{ while ( read item ) {
scan for the first bin that is large enough for item;
if ( found )
place item in that bin;
else
create a new bin for item;
} /* end-while */
}

近似比下降到1.7
Best Fit
就在First Fit基础上,优先选前面剩余体积最多的箱子放
上面三个算法很垃圾,因为是顺序决策,只考虑了过去,没考虑未来
我们称这种一个输入即时进行决策的算法叫在线算法,类似流水线
On-line Algorithms
Place an item before processing the next one, and can NOT change decision
You never know when the input might end.
No on-line algorithm can always give an optimal solution.
【Theorem】There are inputs that force any on-line bin-packing algorithm to use at least 5/3 the optimal number of bins.
即,任何在线算法我们都能设计出一组解,让近似比大于5/3
显然我们有对面的离线算法,就是完成输入才开始决策
Off-line Algorithms
之前写的基本都是离线算法
比如将输入排序后再执行在线算法
The Knapsack Problem — fractional version
背包问题,我们放的东西不仅仅有体积,还有价格,而且还可以切开
但是切开之后,价格会有系数 \(p_i\) 进行修正,使得切了之后总价格减少
我们希望让这个背包里面东西的价格最大
A knapsack with a capacity M is to be packed. Given N items. Each item \(i\) has a weight \(w_i\) and a profit \(p_i\) .
If \(x_i\) is the percentage of the item \(i\) being packed, then the packed profit will be \(p_i x_i\) .
正解算法是,找出性价比最高的物品,能整个放进去就放,不能就切了放进去,然后循环。
在这个解法中,背包里的物品只会有一个被切过,其他都是完整的。
这个问题有一个变种——0-1版本,即物品不能切了,要么放要么不放
The Knapsack Problem — 0-1 version
这是一个NP问题
但是可以通过DP得到精确解
遇事不决先写个 \(F(N)\),发现推不出来,那我们看一下为什么写不出来,发现是无法确定能不能放,就加个剩余体积 \(M\) ,然后讨论一下要不要放,两者取 \(max\) 即可
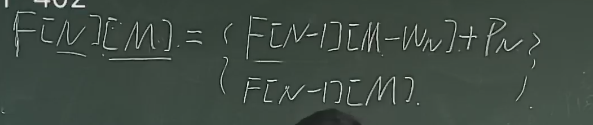
DP复杂度 = 状态转移时间开销 x 状态数
\(O(1) \times O(N) \times O(NM_{max})\)
我们得到了精确解,是不是解决了NP问题
当然不是,注意有 \(M_{max}\) 。即这个复杂度与参数也呈线性关系,这不是一个多项式开销。
The K-center Problem
yy认为整个ADS最美妙的例子
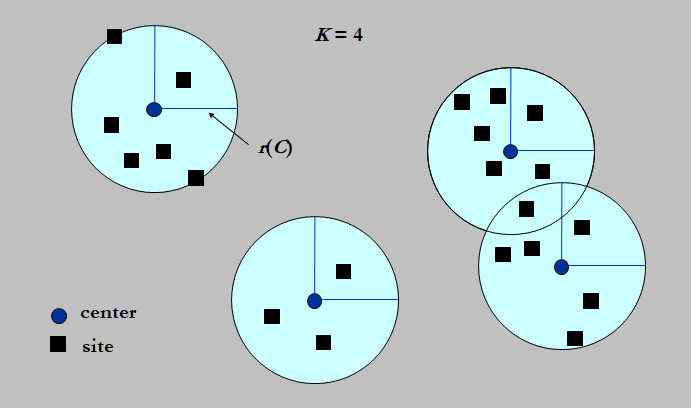
给N个初始点的坐标,给一个数K,要求你找出K个圆心,每个初始点会被囊括近=进距离最近的圆心。如此初始点被分进了K个圆里。
然后对于每个圆,我们找出与圆心最远的初始点,记录该距离。我们希望能够让这个距离最小。
好绕
将初始点当成宿舍或教学楼,圆心当成食堂
规定大家只能就近去食堂,这个问题就是想让干饭跑的最远的那个同学能尽可能少跑
对于欧氏几何,我们有以下前提:
- \(dist(x, x) = 0 \qquad (identity)\)
- \(dist(x, y) = dist(y, x) \qquad (symmetry)\)
- \(dist(x, y) \leq dist(x, z) + dist(z, y) \qquad(triangle inequality)\)
A Greedy Solution
最大边际效应贪心策略,无法解决这个问题,但是思路可以了解
这问题最难的地方就是,圆心可以放在任意地方
面对这种情况,我们就自行加一些约束,比如规定将圆心放在初始点上:
这种约束得到的解近似比不大于2,由三角不等式得出
这个算法有个前提,就是我们已经知道最优解(即半径r)

我们先随便找一个初始点,把半径2r内的点踢出待检测点集,然后再从电集再随机找点,以此类推
递归结束后,我们检查圆心数量是否大于K,如果大于了,我们就能推断出,这个问题的最优解大于r
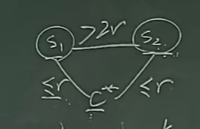
为什么一个随机的算法能推出这么一个确切的结论,我们反证法证明一下
假设我们得到了K+1个圆心,那么一定存在两个选出来的圆心 \(s_1\) 和 \(s_2\),它们被最优解的圆心 \(c^*\) 包含(因为我们选出的圆心在初始点上,K个最优解要包含至少K+1个初始点),就出现矛盾了:
通过这个方法我们能证明原问题是否存在K下的最优解
【Theorem】 Suppose the algorithm selects more than K centers. Then for any set C of size at most K, the covering radius is r(C) > r.
我们还有个问题,怎么求最优解 \(r(C^*)\)。可以用二分法,就丢给这个贪心法
对于这个贪心算法我们得出来的是近似比的上限的两倍(2r),所以近似比是2
A smarter solution — be far away
在上一个算法基础上,我们进一步限制——找离当前点最远的初始点作为新的圆心,而不是在点集里随机找

这个近似比也是2
这个问题最小近似比就是2