Lecture 14 | Parallel Algorithms
高级数据结构与算法分析2024-05-27第3-5节 (zju.edu.cn)
- To describe a parallel algorithm
- Parallel Random Access Machine (PRAM)
- Work-Depth (WD)
Parallel Random Access Machine (PRAM)
我们接下来就用PRAM模型进行描述
下面是PRAM描述并行的伪代码
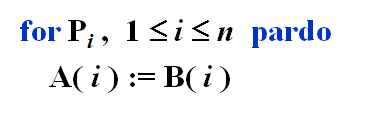
for后面加pardo表示 1~n 的处理器并行执行for语句里面的语句
:=表示赋值,也要占用一个处理器(从内存中取数据)
注意到并行执行的语句有相同处理对象的话可能会造成冲突,我们需要进行限制
- To resolve access conflicts
- Exclusive-Read Exclusive-Write (EREW)
- 禁止同一个mem读写数据,最安全最暴力
- Concurrent-Read Exclusive-Write (CREW)
- 可以同时读,不能同时写
- Concurrent-Read Concurrent-Write (CRCW)
- 可读可写
- 如果造成冲突,我们可以
- Priority rule (P with the smallest number)
- 给所有处理器一个优先级,优先级高的写,低的被覆盖
- Common rule (if all the processors are trying to write the same value)
- 如果两个处理器写的相同就允许,不相同就都禁止
- Priority rule (P with the smallest number)
- Exclusive-Read Exclusive-Write (EREW)
The summation problem
给n个数,让你求和
并行的基本思路是树状求和

圈圈是处理器
这个例子里给了8个处理器计算8个数的和
下面给出PRAM模型下的伪代码

stay idle也是一条语句,指示该处理器暂时闲置这里可见,PRAM模型要求每个时间点的每个处理器都得分配任务,包括闲置
即,PRAM描述的比实际的工作量要冗余很多

于是我们讲讲另一个WD模型
Work-Depth (WD) Presentation

不需要每个处理器都得分配任务了,会自动执行其它工作或自动闲置
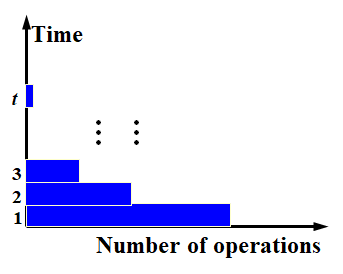
WD任意时间都可以有任意工作量

Measuring the performance
评价并行算法需要考虑两个因素
- Work load
- total number of operations: W(n)
- Worst-case running time: T(n)
类似工作量和工期
注意串行算法我们没有考虑工作量
由这两个因素我们得出以下的指标:
- W(n) operations and T(n) time
- T时间里完成的W工作量
- P(n) = W(n)/T(n) processors and T(n) time
- T时间、P处理器数量
- on a PRAM,不能用于WD模型
- W(n)/p time using any number of p ≤ W(n)/T(n) processors
- 这个算法能支持W(n)/T(n)个处理器,但是手上没这么多处理器,只有p个
- on a PRAM,不能用于WD模型
- W(n)/p + T(n) time using any number of p processors
- 分情况
- 如果p很大,那么这个式子就是T(n),表示算法支持的最大处理器数量下的耗时
- r如果p很小,那就是W(n)/p,同第三个
- on a PRAM,不能用于WD模型
- 分情况
上面四个是 All asymptotically equivalent 渐进等价的
至于为什么后面三个只能用于PRAM,因为PRAM将所有处理器平等对待的,工作量相等的,而WD模型会根据处理器情况,让好的多干点
再次强调PRAM中,处理器空闲也算工作量,而WD不算,所以PRAM所有处理器工作量一样
看回那个求和例子,下面是WD模型的

Prefix-Sums
求1~n的所有前缀和
首先,坐标是(h,i),表示h高度下的第i个结点
每个结点有个B值,表示当前结点的和
内部节点有C值,表示当前结点所在子树右路径上最深的结点的前缀和
很绕,但设计的思路很顺畅
我们希望通过层层递进的方式求出结果,那么我们需要一个每一层之间传递前缀和结果的载体,这就是C
选右叶子而不是左叶子是为了美感hhh

注意到,左路径上,i=1有B=C
右儿子上,i为偶数有C=其父节点C
还剩非左路径的左儿子,其等于自身B+同一层左边结点的C
为了实现并行,我们微调,取其同一层左边结点父节点的C
注意我们实际的表达式,微调了依赖关系,让同一层的计算不会相互依赖,达到并行效果
下面是WD模型的算法

Merging
merge two non-decreasing arrays A(1), A(2), …, A(n) and B(1), B(2), …, B(m) into another non-decreasing array C(1), C(2), …, C(n+m)
给两个递增序列,通过归并合并两个数组为一个递增序列
我们要用到切分法
Technique: Partitioning
就是将问题切分为能并行解决的子问题再整合,类似分治法
我们假设A序列和B序列元素唯一、长度一致、logn为整数
我们定义一个 \(RANK(j,A)\),表示 \(B(j)\) 大于 \(A\) 中的前 \(RANK(j,A)\) 个元素
- RANK( j, A) = i, if A(i) < B(j) < A(i + 1), for 1 \(\le\) i < n
- RANK( j, A) = 0, if B(j) < A(1)
- RANK( j, A) = n, if B(j) > A(n)
由此我们能得到很简单的排序算法

现在的问题是怎么求RANK,我们可以二分法
注意到每个元素的二分是相互独立的,所有可以并行求解

关于右边的顺序查找
注意到RANK值之间有关联,即后面的RANK不会小于前面的RANK
于是我们可以压缩范围
而且,而且,而且!!!我们可以双向并行查找,不是pardo哈我意思是双线进行
A指针的数值比B的要小,就能求出这里的C(A)了,反之就能求出这里的C(B)
反之仔细看右边的代码
不过这样有边界情况,技巧是两个序列末尾都加个无穷大的数
Parallel Ranking
Stage 1: Partitioning
子问题数量为 \(p=n/logn\),怎么来的先不管,是根据目标反推出来的
然后我们取logn为间隔选出一些元素,作为每个元素的开头
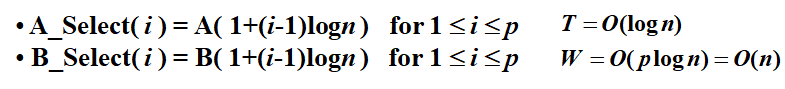
算出这些选出元素的RANK,下面图中的蓝线和红线即被选出的RANK
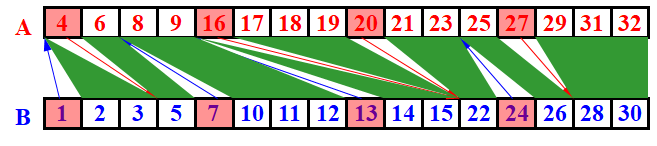
然后我们将两条线之间的元素划为一个子问题,即每个绿色区域,分别计算里面的RANK
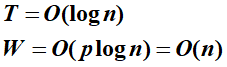
Stage 2: Actual Ranking
At most 2p smaller sized (O(logn)) problems.
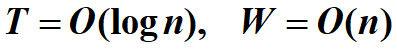
Maximum Finding.
就是从序列中找出最大值
如果用求和的方式并行可以解决,但是
Compare all pairs
直接全部比较,时间开销直接 \(O(1)\),但是work load 达到 n 方

A Doubly-logarithmic Paradigm
我们先拆分为 \(\sqrt{N}\) 个子问题,每个子问题找出最大值,然后从这些局部最大值中找出最大值
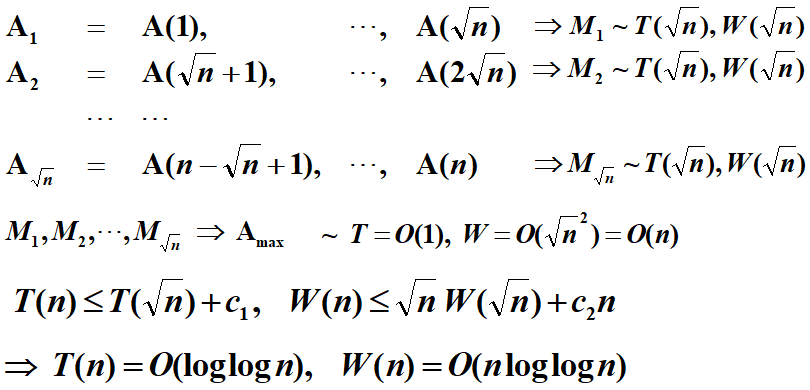
我们再试试按 \(h=loglogn\) 切分,每个子问题很小,直接串行解决就行
我们得到局部最大值后,再按照上面分为\(\sqrt{N}\) 个子问题的算法来求出最终的最大值
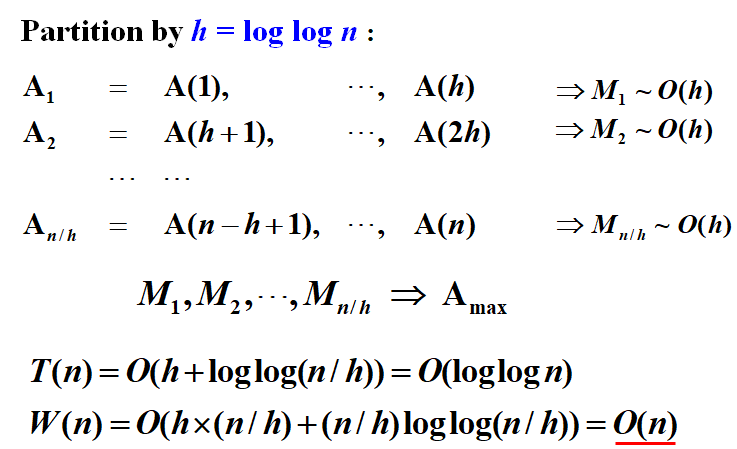
Random Sampling
?????????????
我们开一个新数组 \(B\)
让 \(M=n^{7/8}\) 个处理器各自从 \(A\) 中随机采样一个元素,放到自己对应的 \(B\) 中的位置
然后设置子问题规模为 \(n^{1/8}\),进行第一次拆分处理

然后对于得出的局部最大值,进行第二轮拆分处理

我们得到了最大值,但是,我们只是采样了部分元素,这些元素还可能是重复的
但是我们可以将采样最大值与全部元素检查,如果没有更大的就完事了,如果有就将这些更大的随机放进B,重新进行这个算法,直到完事
注意只能随机放入B,因为是并行比较,可能出现覆盖情况
随机算法都是精确算法,时间复杂度都是期望值