Lecture 9 | Greedy Algorithms
贪心算法用来解决优化问题
给定一个目标函数/优化函数(optimization function),取值有限制(constraints),限制下的子空间叫 feasible solutions,我们希望在限制下求一组使得函数值最大化/最小化的最优解(optimal solution)
The Greedy Method: Make the best decision at each stage, under some greedy criterion.
A decision made in one stage is not changed in a later stage.
贪心算法简单来说,就是,面对规模为N的子问题,我们类似分治拆分为子问题,一般是让规模减少1,然后让N-1的最优解加上按某策略得到的元素,就是N得最优解
比如,我们要从北门去南门,我们贪心策略就是就每到一个路口就往南走
贪心算法需要在以下两条件下才适用:
- 全局最优解(global optimum)等于局部最优解(local optimum)之和
- 全局不等于局部和,但是因为贪心算法效率高,可以用来求近似解
Greedy algorithm works only if the local optimum is equal to the global optimum.
DP有套路,贪心没套路,更难
Activity Selection Problem
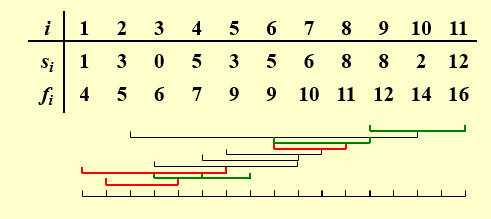
n个活动不同时间段,不能重叠,看怎么分配时间以最大化利用时间
\(s_i\)表示开始时间,\(f_i\)表示结束时间
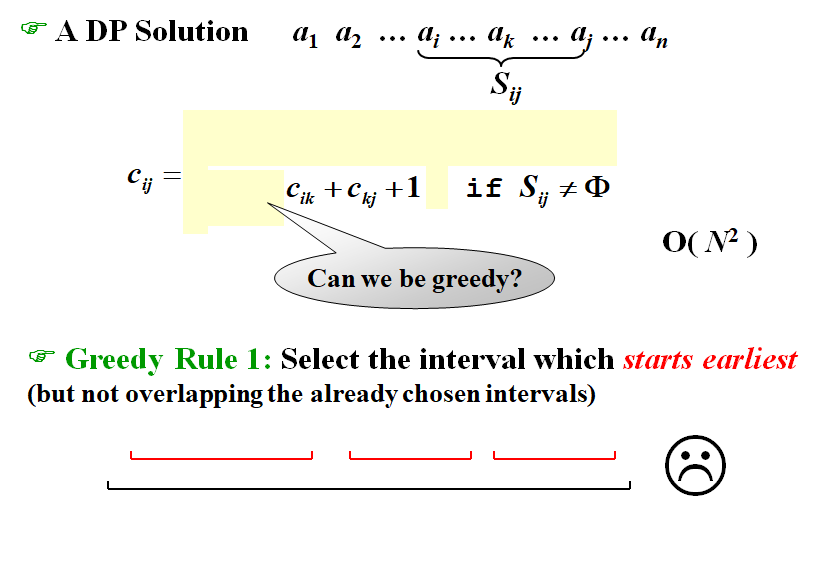
首先对这个问题试了下DP
最简单粗暴的就是 \(c_{ij}=max(c_{ik}+c_{kj}+1), 如果ij区间不为空集;否则c_{ij} =0\)
但是很垃圾,会有重复,而且有顺序成本
注意,ij应该取开区间,即 \(c_{ij}表示的是a_i之后,a_j之前,不包括a_i, a_j\)
第一个贪心策略:选 \(s_i\) 小的。显然不行
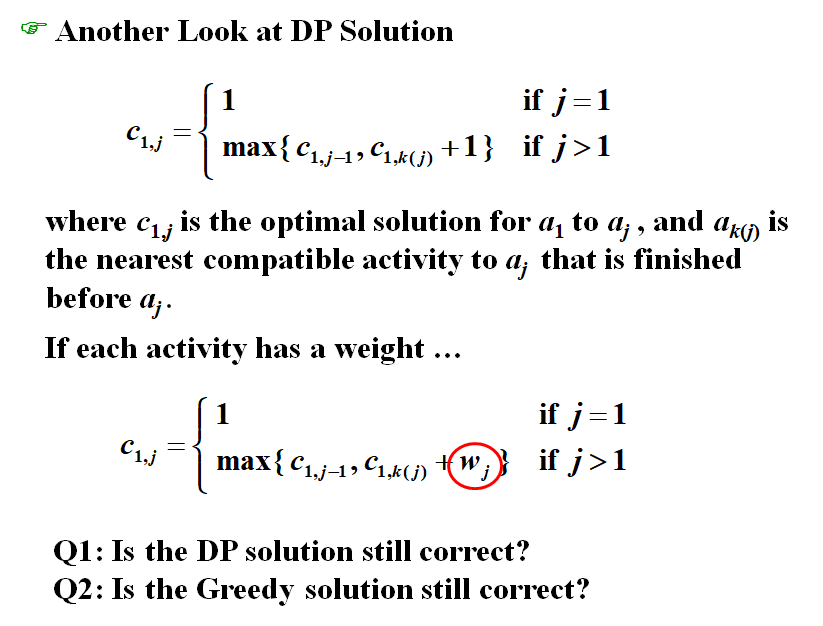
一个更好的DP
刚刚的二维DP有排序冗余。即会通过不同顺序得到同一个解,这太浪费算力了
题目是集合选择问题,我们这里变成序列选择问题
我们可以定义顺序,即子问题和父问题按照一定顺序拓展开来,比如往前 \(i\) 问题的加上第 \(i+1\) 个元素,关注新增的元素即可,即分类讨论加入新元素和不加入新元素
上面那个就是新的状态转移方程
下面是拓展问题,就是每个活动有了权重
有错误,边界条件不是1,是权重
有权重后刚刚的贪心策略也不能用了
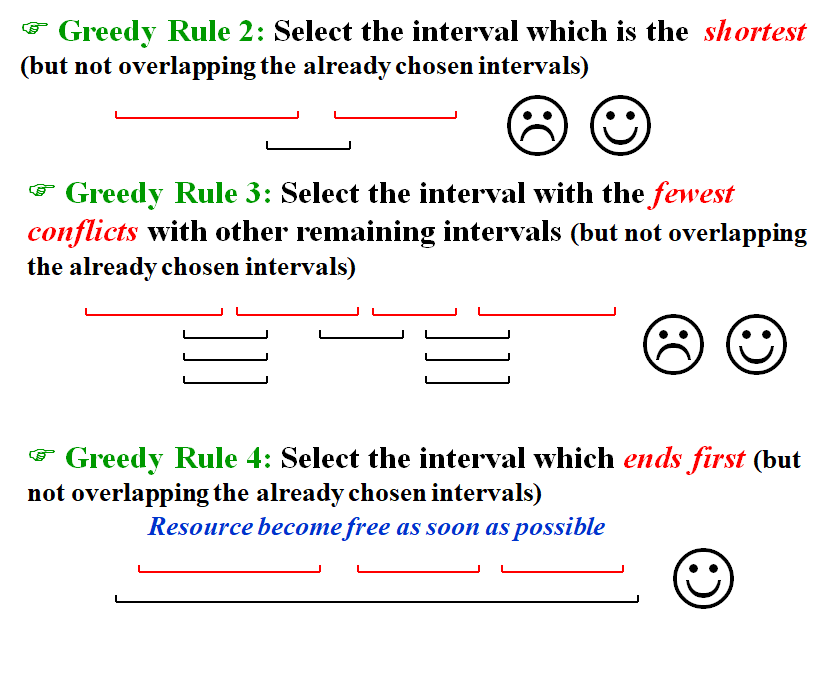
策略二:选时间短的,显然不行
策略三:选与其它线段冲突少的
策略四:选最早结束得--》最优解。前面的例子都能通过

贪心算法难就难在选出这种策略,以及证明这种策略能得到最优解
后者需要证明两点
- 证明是可行解
- 证明是最优解
证明思路与DP证明最优子结构类似,用反证法
对于得到的解,我们将第一个元素换成别的,然后证明换了之后不会比我们得到的解要好
注意,替换后不能影响后面的元素

对于一个贪心策略是否可行,具体要证明三点
- 能得到可行解
- 策略选出的第一个元素会被最优解包含,即可以替代最优解的元素
- 就是每一个子问题得到的元素都包含在最优解里的,因为每一层都是一个新的问题,会得到一个新的第一个元素
- 证明是最优子结构
Huffman Codes – for file compression
没看