Lecture 2.2
Chap 3 arithmetic for computer
3.2 有符号数与无符号数
本章主要是复习数逻的基础内容
阿姆达尔定律!!!
3.1 Introduction
- Computer words are composed of bits;
- one word is a vector of binary numbers
- there are 32bit/word or 64bits/word in RISC-V
- 32 bits, as a word, contains four bytes
- Generic Implementation of Arithmetic
- use program counter (PC) to link to instruction address
- fetch the instruction from memory
- the instruction tells what needs to be done
- ALU will perform the specified arithmetic operations
3.2 unsigned and signed
在有符号数中,最高位所代表的值是- 2^ 31 ,而不是-1
有符号数在计算机中通常用补码表示,我们是不能直接读出其真值的。对其非符号位取补后就得到了符号位+真值的原码。
注意,电脑里面存储的负数的二进制码是补码的形式,人类要阅读需要对其取补以获得原码,是这个意思。
所以有符号数1001到底到底是-1还是-7?得看题目说这是原码还是补码。
有点懵
有的计算机使用补码表示,有的使用原码或反码
前者取补码可得结果,后者取第一位是符号位可得结果
但是,在大多数现代计算机系统中,有符号数都使用补码表示。
什么是真值
真值就是真正的值。将带符号位的机器数对应的真正数值称为机器数的真值。
0000 0001的真值= +000 0001,1000 0001的真值= –000 0001。
原码
就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值。
反码
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反
补码
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1
-1 和 0xFFFFFFFF问题
有符号 -1 的二进制表示就是以补码形式表示,即: 0xffffffff ( =2 ^ 31 +2 ^ 30+…+2 ^ 1+2 ^ 0=- 2 ^ 31+2 ^ 31-1=-1)
unsigned (-1)表示无符号整数的最大值 即: 4294967295(二进制全1) 因此,unsigned(-1)=1,111…111(共32个1)。表示unsigned的最大值。 也就是0xFFFFFFFF
3.3 Addition
半加器与全加器
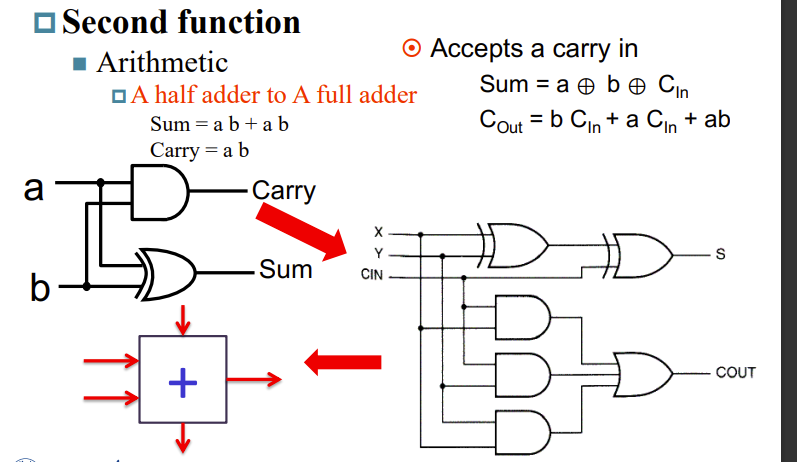
左下角是全加器的简写
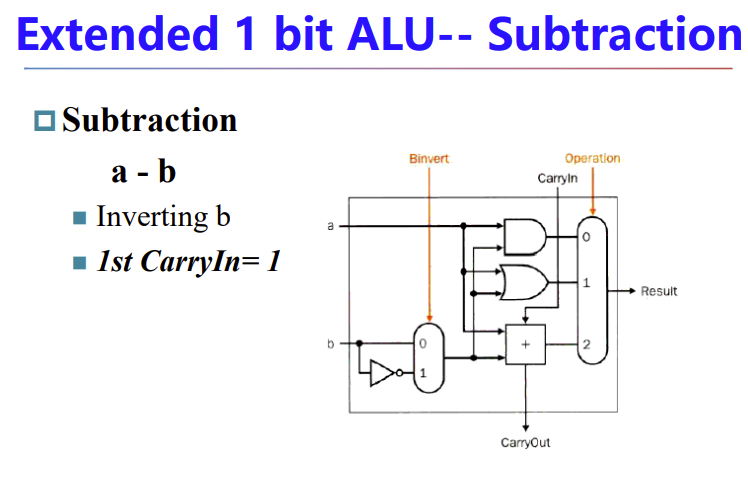
ALU

再加入减法
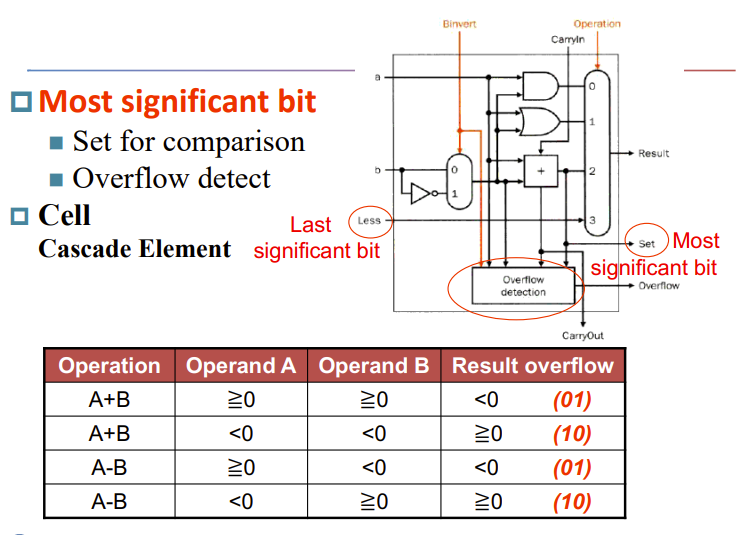
再加入溢出检测
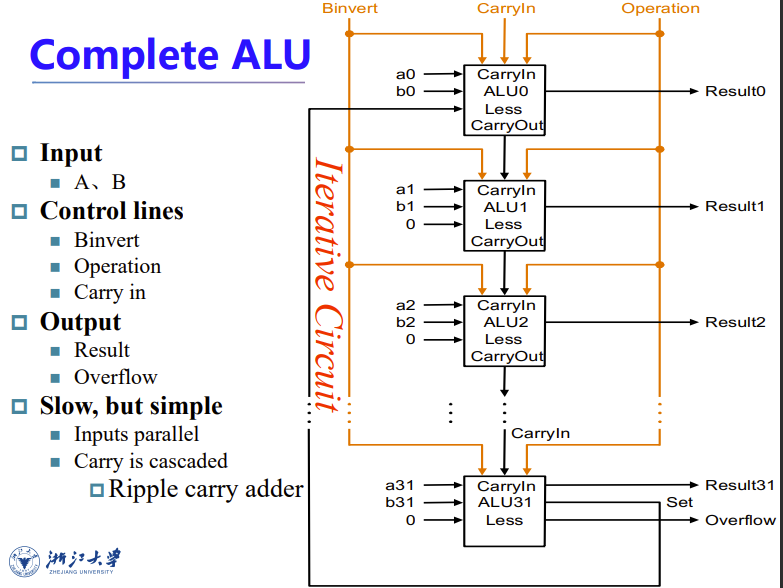
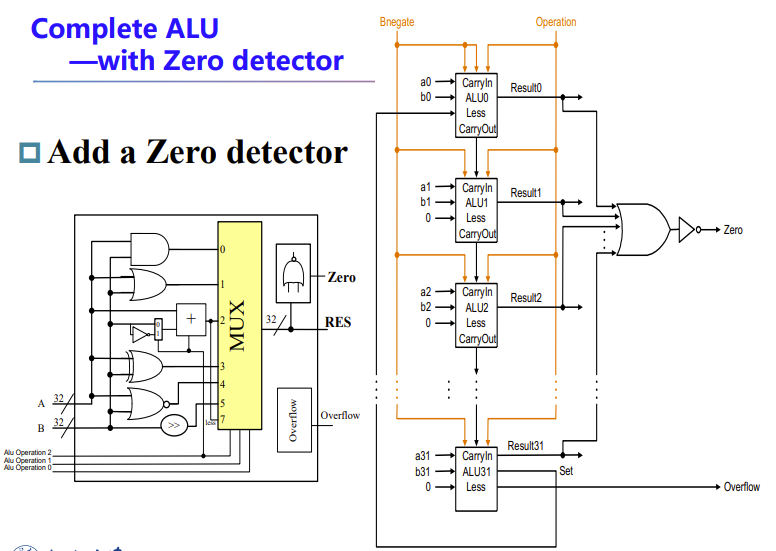
并行输入,串行输出,得到完整ALU
再加一个zero detector
这东西就是看计算结果是不是0, 是为了加速数的比较运算,比较的时候需要先检测数是不是0
?
用下面这个东西表示ALU,右边列举标准的操作集合
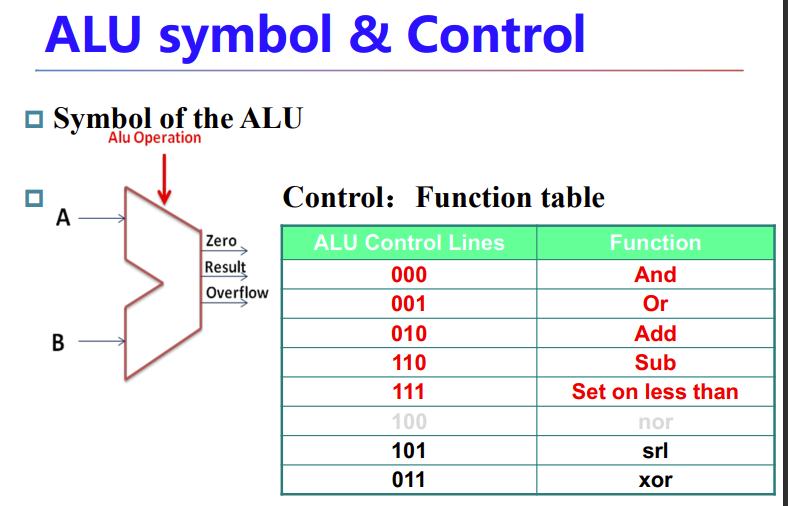
srl = shift right logic,逻辑右移
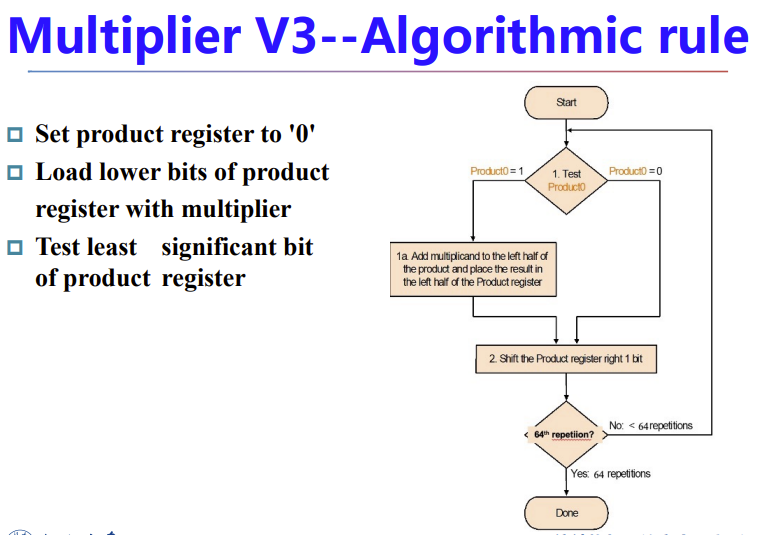
3.4 Multiplication

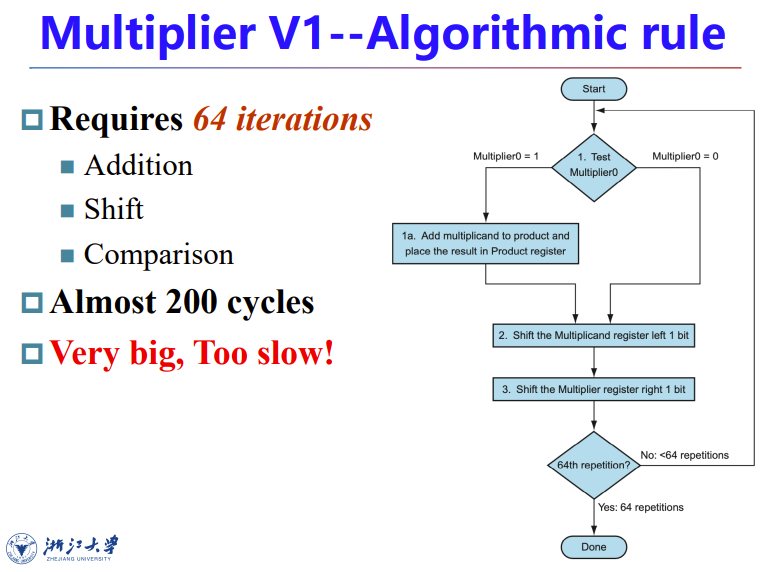
由此我们可以设计出简单的电路图与算法:
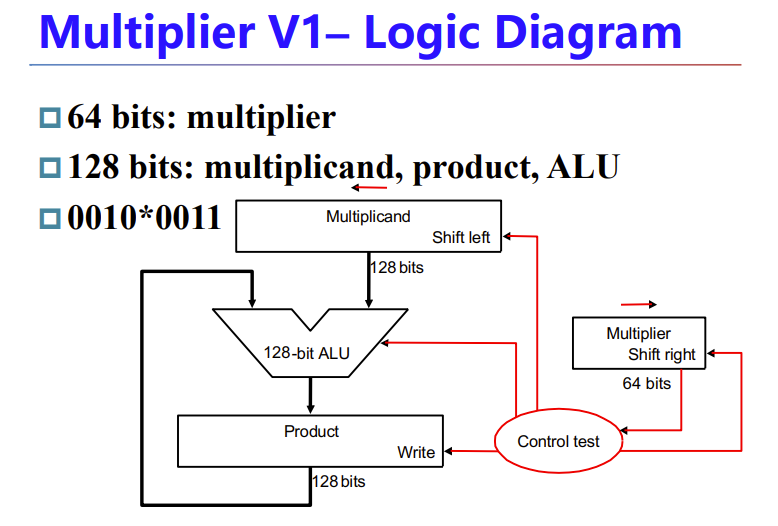
每次检测乘数的LSB,0就让结果加0,1就让结果加被乘数。然后被乘数左移一位,乘数右移一位
64bit乘法用128bit是因为乘法最大情况会使位数翻倍
显然这玩意儿太大太慢了,用了320bit寄存器
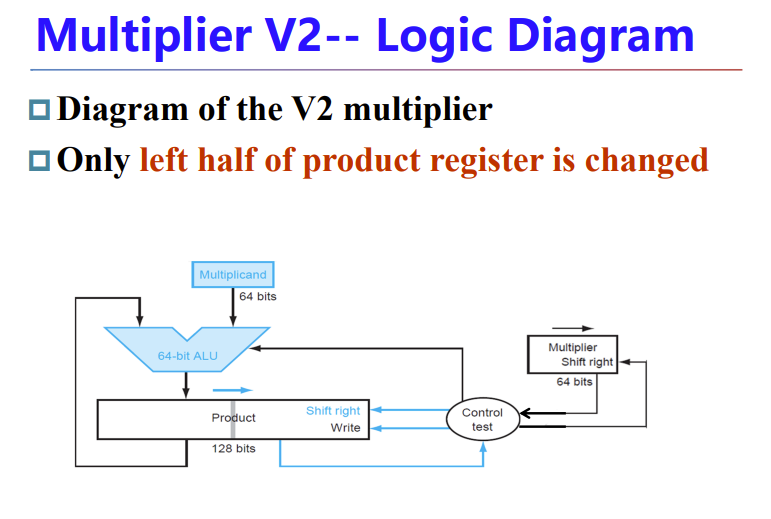
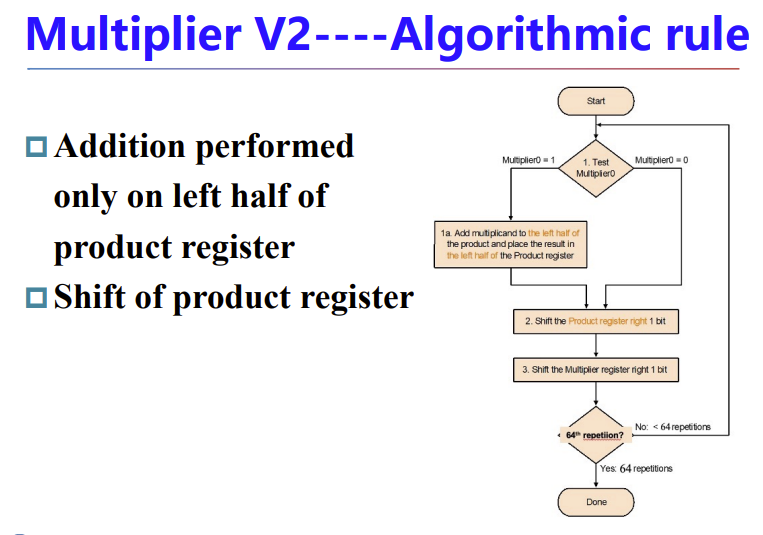
改进一下算法,从移位被乘数改成移位乘积,当然乘数依旧移位。从而得到第二版本的乘法算法。

将每一轮的乘积放入128bit寄存器的左边,然后寄存器整体右移一位,欧克。
这样寄存器大小减少到了256bit
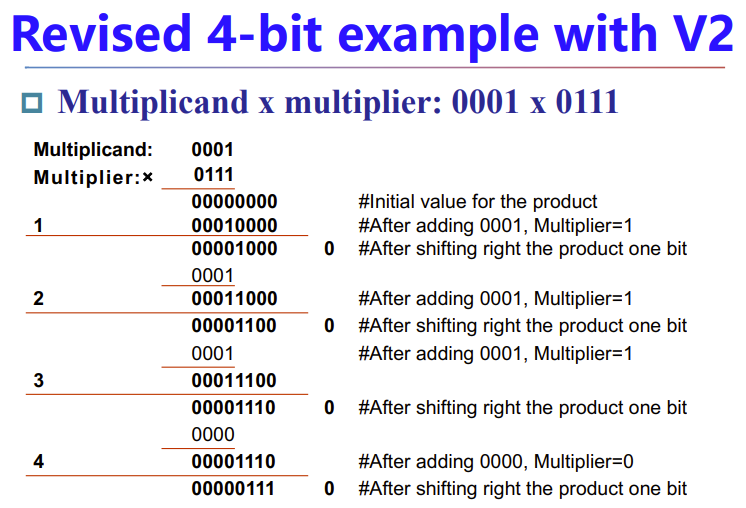
下面是个例子
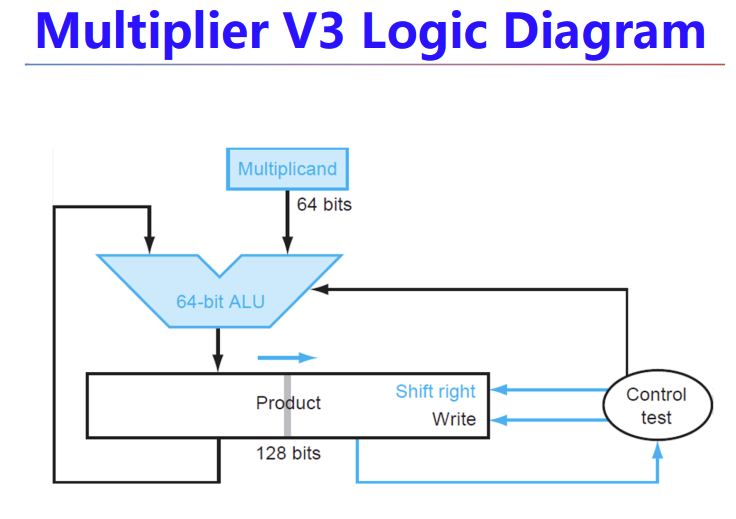
不过或许我们可以再优化一下,从V1到V2我们实现的实际上是减少同一时间点空闲的寄存器bit,这也是我们优化的思路。
而放乘积的128bit寄存器大部分时间也空着很多bit。
于是,我们可以将乘数一开始放在128bit寄存器右边,与乘积和一起右移。


有符号数乘法
储存符号位,然后转化为无符号数,计算,然后比较符号位

Booth‘s Algorithm
乘数和被乘数1很多的话算的很复杂,如果能够减少1的数量就可以大大优化
于是我们可以凑,加一个数减一个数,将挨在一起的1减少为一个1

