Skip to content

Lecture 3

:material-circle-edit-outline: 约 637 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

Booth' algorithm

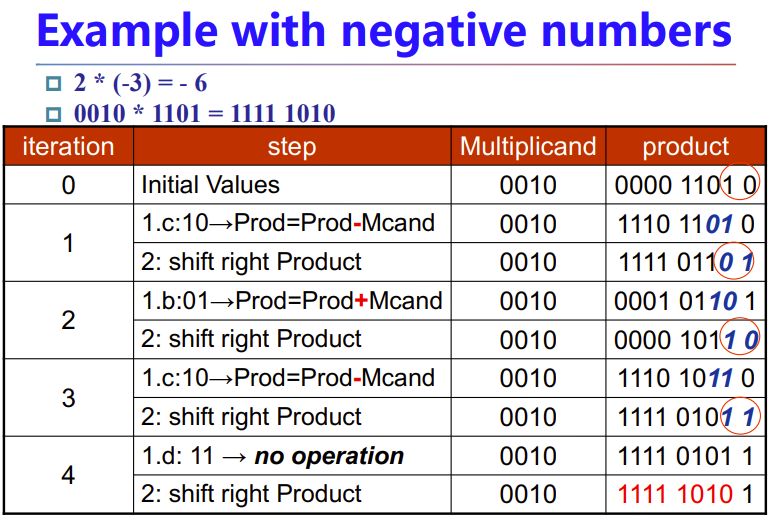
布斯（booth）算法：面向一比较多的二进制乘法，加法+减法

  1. 对于两个乘数，单独的1就拆出来为单独的数，挨在一起的1整体拆出来。如10111 -> 10000+111
  2. 然后加一个小的数消除挨一起的1。如111+1-1 = 1000-1

布斯算法支持两个有符号数直接当成无符号数算，不用管符号位。之前的乘法算法不行

image-20240314092252984

image-20240314092416065

image-20240314092458638

image-20240314092448272

现有的数据通路大多低于64bit，所以乘法需要进行分解

image-20240314103326608

3.5 Division

最基础的算法就是将除法看成多次减法，大就减

乘法从低位开始算，除法从高位

需要再看一下

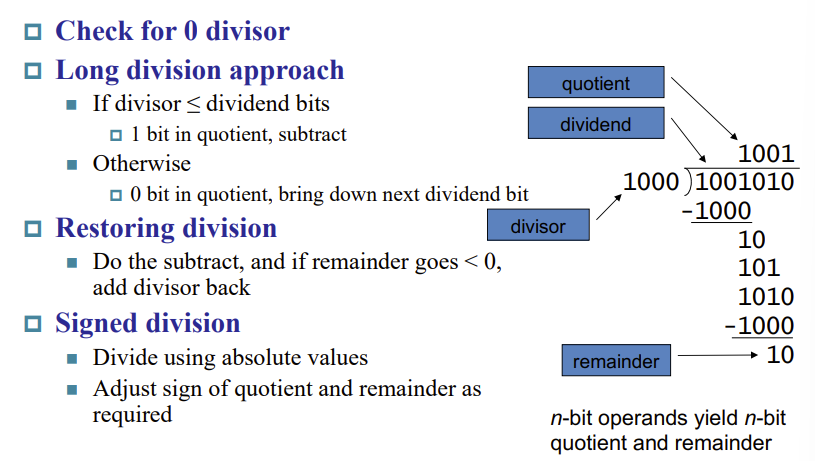
image-20240314192042799

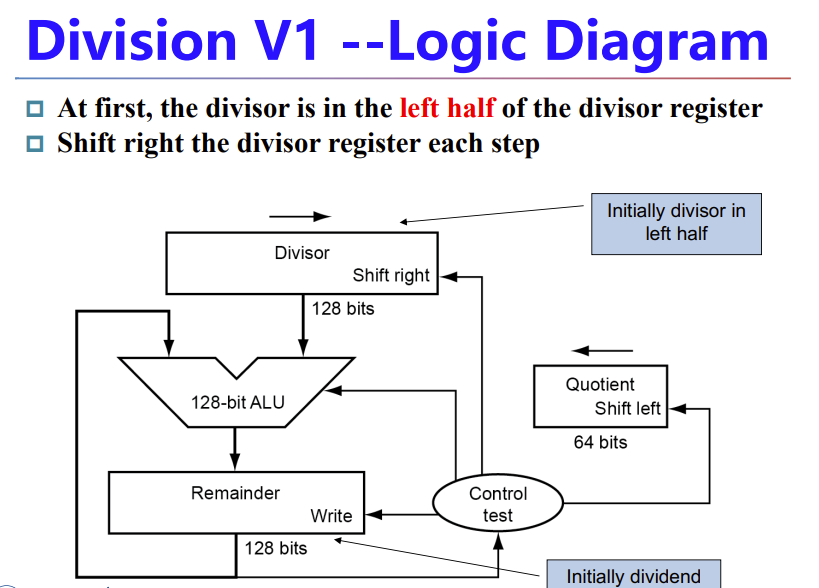
image-20240314192227788

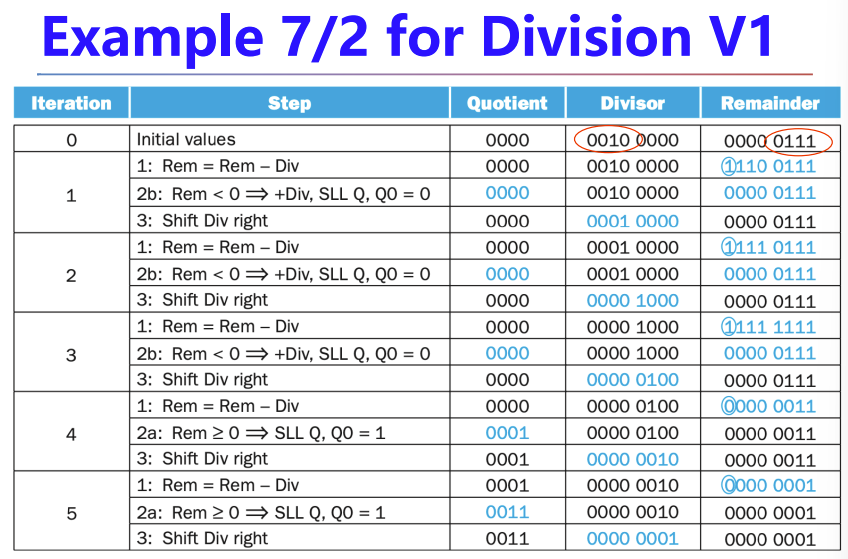
image-20240314192530597

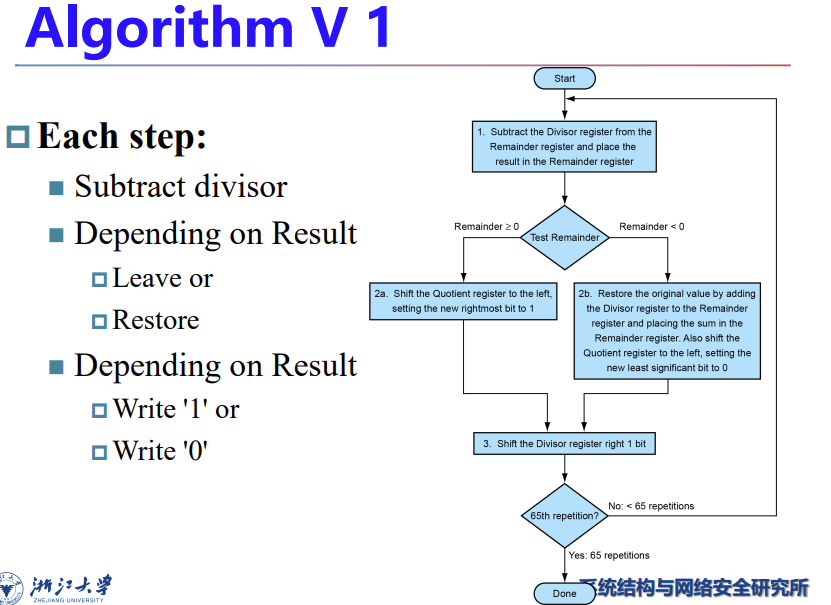
image-20240314192449035

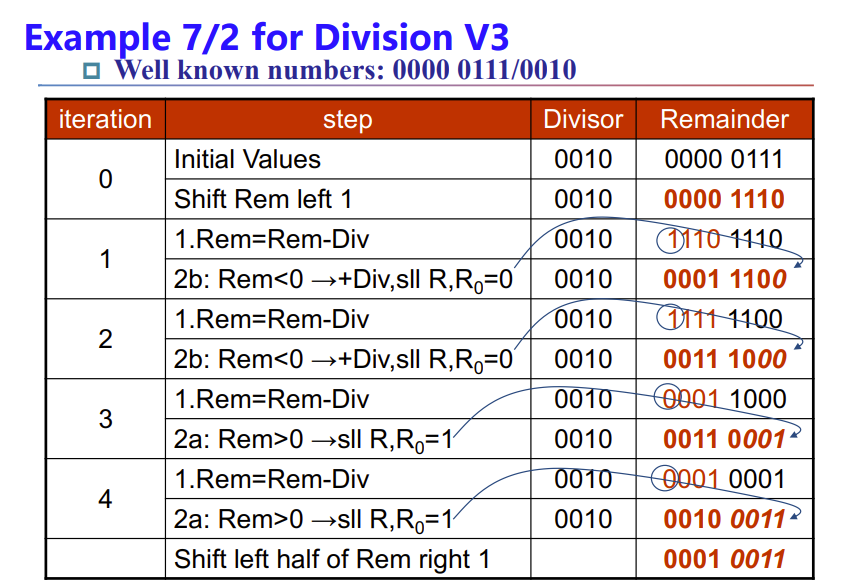
类似乘法的优化思路：

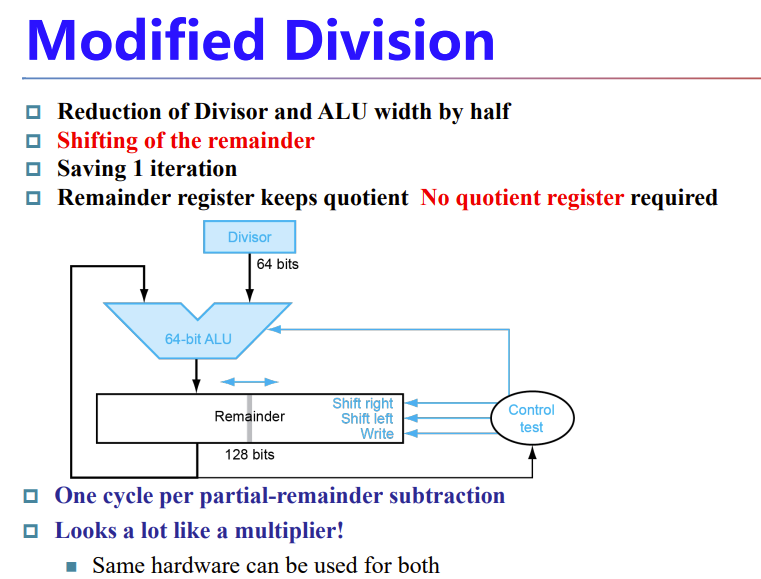
image-20240314193121963

注意，优化后的算法在算完后要再对remainder的左半部分做一次右移运算，不然remainder会大2两倍

image-20240314193231533

Signed division

商的符号判断和乘法一样

余数的符号跟着被除数

image-20240314193322111

image-20240314193405465

image-20240314193947521

  • 除法不能并行处理，因为 “除尽” 这件事不确定，下一位的运算依赖上一位的余数
    • 可以predict一下，比如查表
  • 至于除数是0的情况，可以通过软件避免，所以硬件没有涉及
  • 溢出也没涉及
    • common fast，没必要为了除法增加硬件
    • 根据阿姆达尔定理，主要加快加法即可

上面的算法都是针对int，实际上用的更多的是浮点数

3.6 Floating point numbers

image-20240314194918781

下图中summary -> significand 改成 fraction 更清晰，即小数点后的部分

image-20240314195358149

  • 因为这样计数第一位肯定是1，所以直接省略了第一位的1
  • summary是如何得到一个浮点数的真值
  • 注意有个bias：
    • 单精度要加127，双精度要加1023，这样就都是正数了

image-20240314200015365

image-20240314200248035

保留用于表示溢出，不能用于表示数值

考试会考某种情况下能达到的最高精度、最低精度、最大值、最小值

image-20240314200829258

注意两者范围与精度，前者与exponent相关，后者与fraction相关

image-20240314201007808

溢出还行，反向溢出是因为精度的限制，小于最低精度

前者上溢出，后者下溢出

image-20240314201020146

image-20240314201110870

前者上溢出情况，后者约定

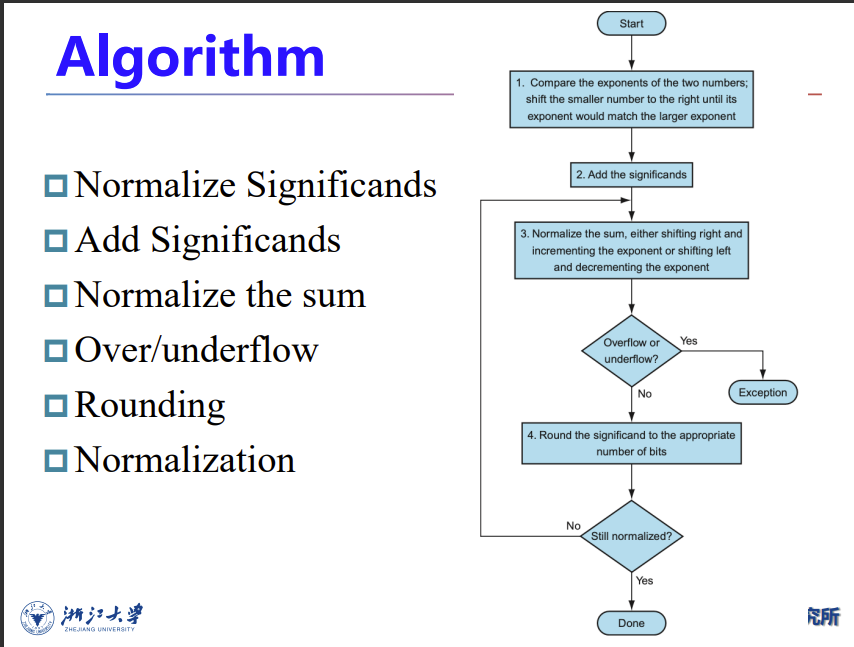
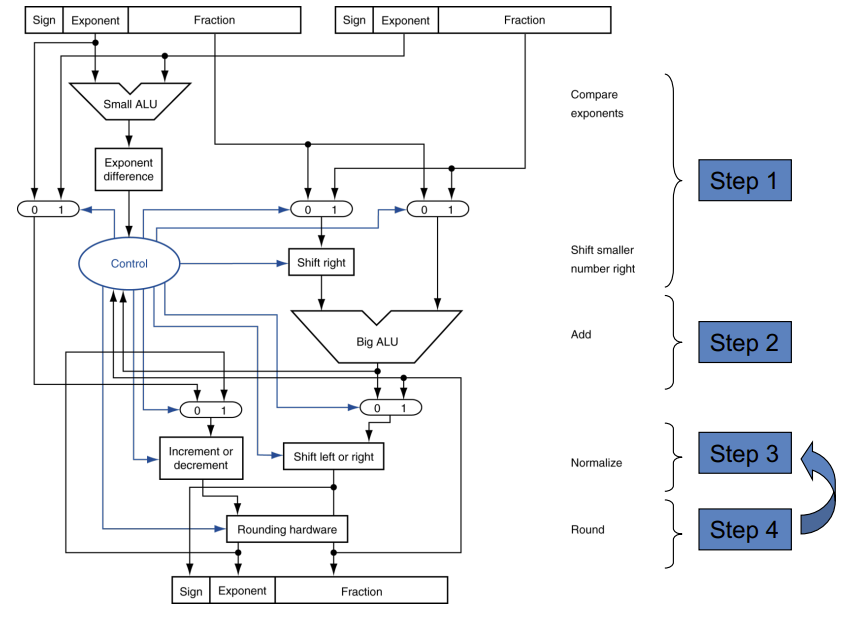
Floating point addition

image-20240314204335778

下面是十进制科学计数法运算的示例，注意truncation、normalization和rounding三个操作

image-20240314204345729

移位都是移小的，因为位数固定的情况下得大的左移小的右移，大的数左移MSB没了之后误差更大，小的右移LSB影响小

image-20240314204507055

image-20240314204427025

image-20240314205322024