REVIEW Chap3
240402
arithmetic for computer
Basic Concept
words
- one word is a vector of binary numbers
- there are 32bit/word or 64bits/word in RISC-V
bytes
- 1 byte contains 8 bits
- 32 bits, as a word, contains four bytes
Generic Implementation of Arithmetic
- use program counter (PC) to link to instruction address
unsigned and signed
有符号数
在有符号数中,符号位可以当成值为- 2^ 31 来计算
有符号数取补码时不要操作符号位,只操作符号位之外的位
电脑里面存储的负数的二进制码是补码的形式,人类要阅读需要对其取补以获得原码
有符号数1001到底到底是-1还是-7?得看题目说这是原码还是补码。
各种概念
真值
真值就是实际表示的数值
原码
就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值。
反码
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反
补码
正数的补码是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后
ALU的实现
半加器与全加器
半加器
逻辑表达式 $$ S=\overline{X}Y+X\overline{Y}=X⊕Y\C=XY $$ 真值表
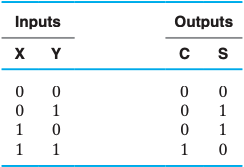
电路图
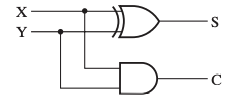
全加器
逻辑表达式 $$ S= \overline{X}
\overline{Y} Z+ \overline{X} Y \overline{Z} +X \overline{Y}
\overline{Z} +XYZ \ C=XY+XZ+YZ $$ 逻辑表达式(with XOR) $$ S=(X⊕Y)⊕Z \C=XY+Z(X⊕Y) $$
真值表
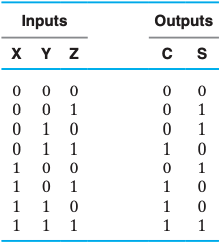
卡诺图
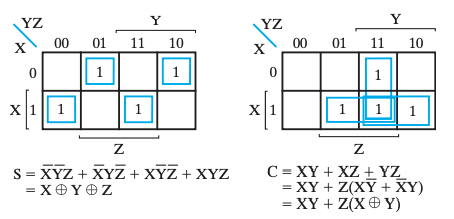
ALU
从1bit的ALU开始
包含 与或加、进位 四个功能

再加入减法
减法的实现就是将两个数转化为补码相加,得到的结果也是补码,需要再取一次补码才是真正的结果
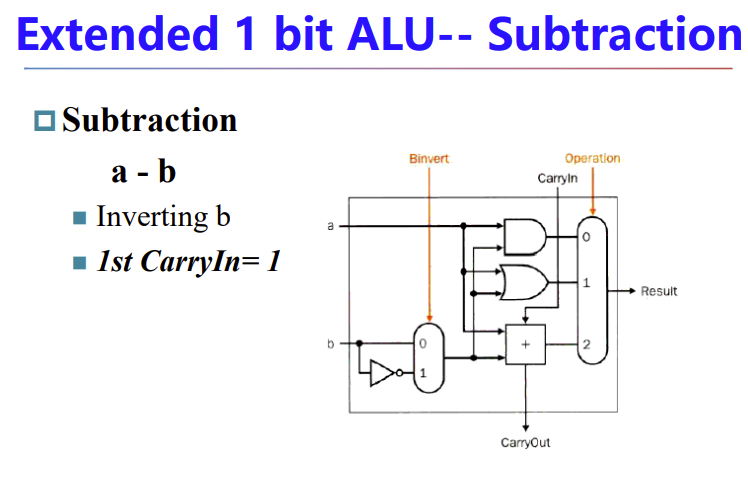
再加入溢出
关于ALU中加法器最高位的溢出检测(进位输入与进位输出的异或)_进位输出cout怎么判断-CSDN博客
-
溢出的概念
- 溢出:overflow,运算结果超出了正常的表示范围
-
溢出仅针对有符号数的运算
- 两个正数相加,结果为负数
- 两个负数相加,结果为正数
无符号数不存在溢出
因为最高位不是符号位,CarryOut能够记录溢出的这一位,合并到最终的结果里
正数相加的溢出与进位的关系
正数是有符号数,因此最高位为符号位 = 0
有符号正数不会发生进位,只会出现溢出
例如:0100 + 0100 = 1000 (对应有符号数 4 + 4 = -8),这就是溢出:两个正数相加得到了一个负数
两负数相加的进位与溢出
负数是有符号数,最高位为1
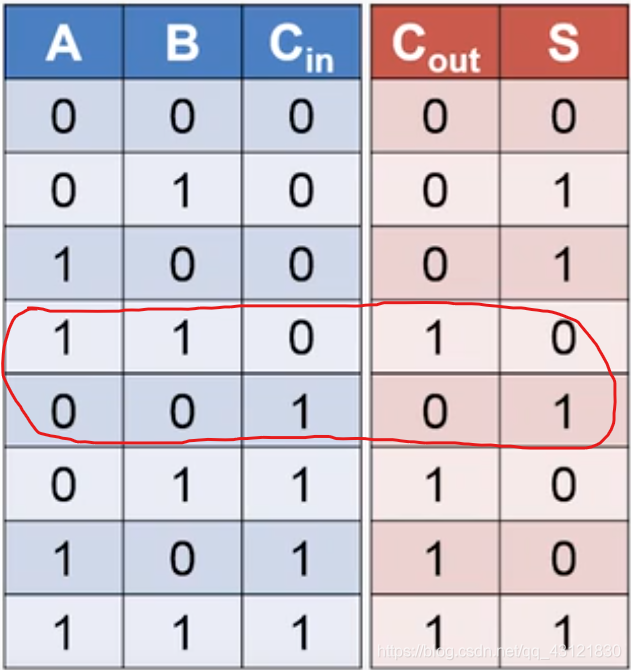
- 溢出情况(实质上下面两种是一种情况,见最后的真值表)
- 1000 + 1000 = 1 0000 ( -8 + -8 = 0)
- 1100 + 1000 = 1 0100 (-4 + -8 = 4)
- 进位情况
- 1100 + 1100 = 1 1000(-4 + -4 = -8)
标注出的两种情况会发生溢出,相应已经在上面的3个问题中举出了例子
得出结论使用一个异或器就可以完成对于加法器中的溢出判断???
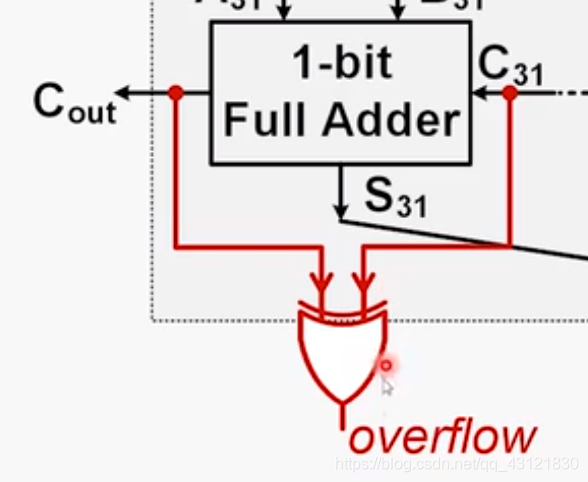
并行输入,串行输出,得到完整ALU
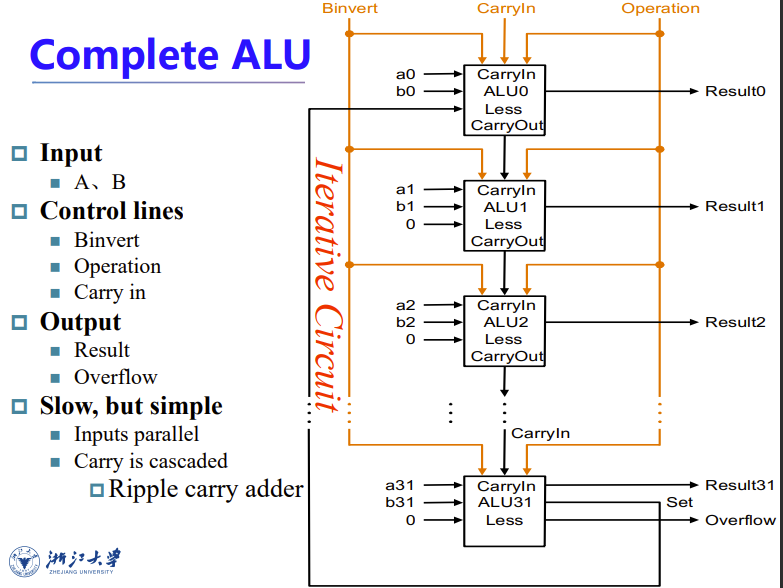
再加一个zero detector
这东西就是看计算结果是不是0, 是为了加速数的比较运算,因为比较的时候需要先检测数是不是0
用下面这个东西表示ALU,右边列举标准的操作集合
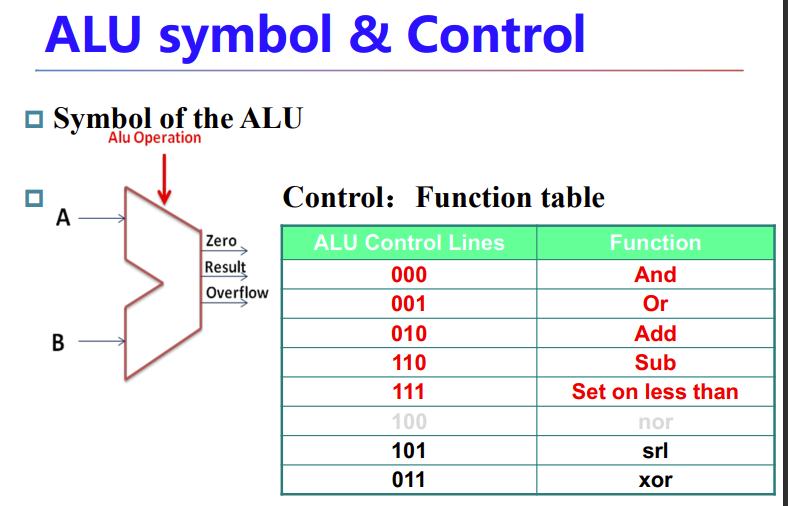
srl = shift right logic,逻辑右移
乘法的实现
multiplier: 乘数
multiplicand: 被乘数
product:乘积
我们需要实现的是64bit x 64bit的乘法
算法
V1版本
V1的思路简单粗暴
手算乘法是乘数的每一位乘整个被乘数,然后移位相加。
下面提到的multiplier、product和multiplicand都是指相应的寄存器
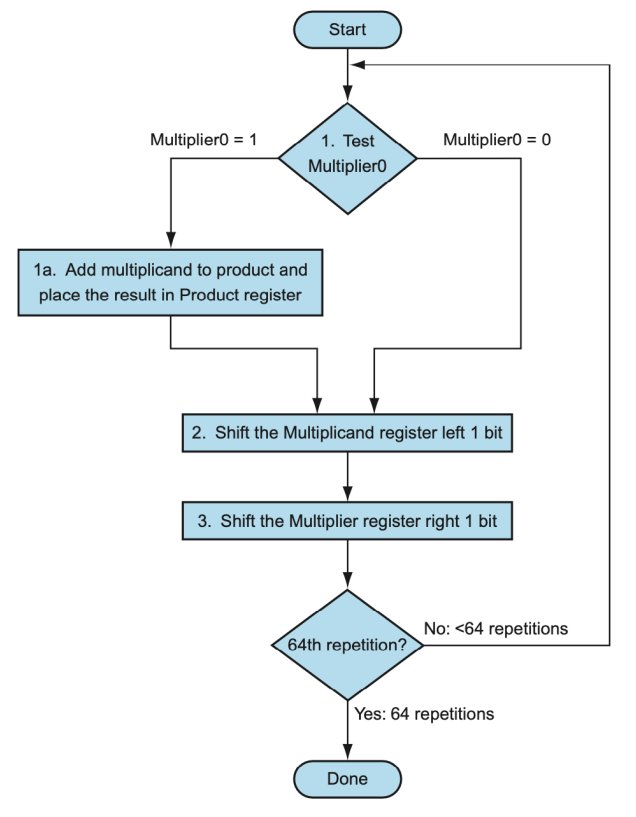
- 每一轮迭代先检测multiplier的LSB
- 如果是0就直接进入下一轮循环
- 如果是1就让product加上当前的multiplicand
- 由此可得到,结束运算的标志是迭代了64次
- 执行完后,准备进入下一轮迭代
- 先右移multiplier
- 模拟手算中选择前一位乘数
- 以及左移multiplicand
- 因为是将multiplicand直接加进product,所以通过左移来模拟手算的偏移
- 先右移multiplier
- 迭代64次后输出product作为结果
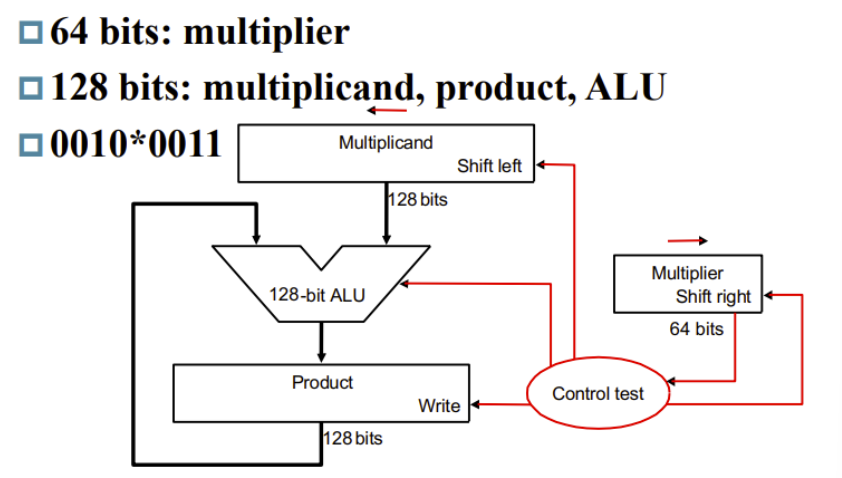
V1使用了320bit reg,而且迭代了64轮,简单粗暴但又臭又长
V2版本
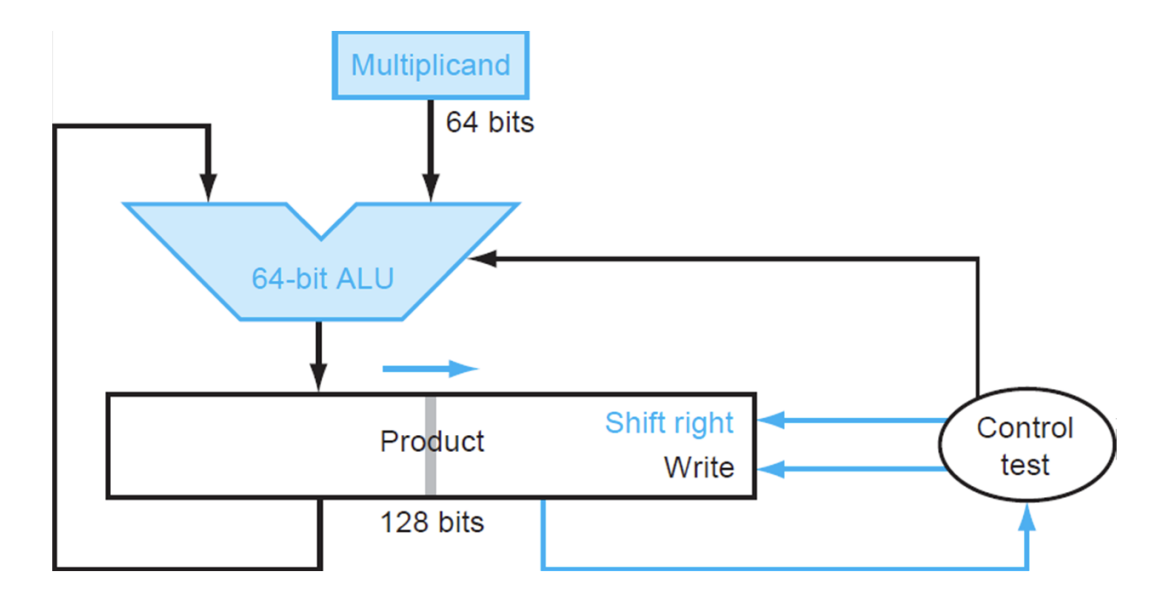
改进思路:偏移的实现从 左移multiplicand 改成 右移product
ALU只需64bit,每轮ALU的输入和输出对象都是product的高半边
输入只需左半边,不懂就想手算中偏移后最后一位都不会参与运算
如此,只需要64bit的ALU和64bit的multiplicand,减少了128bit的reg使用
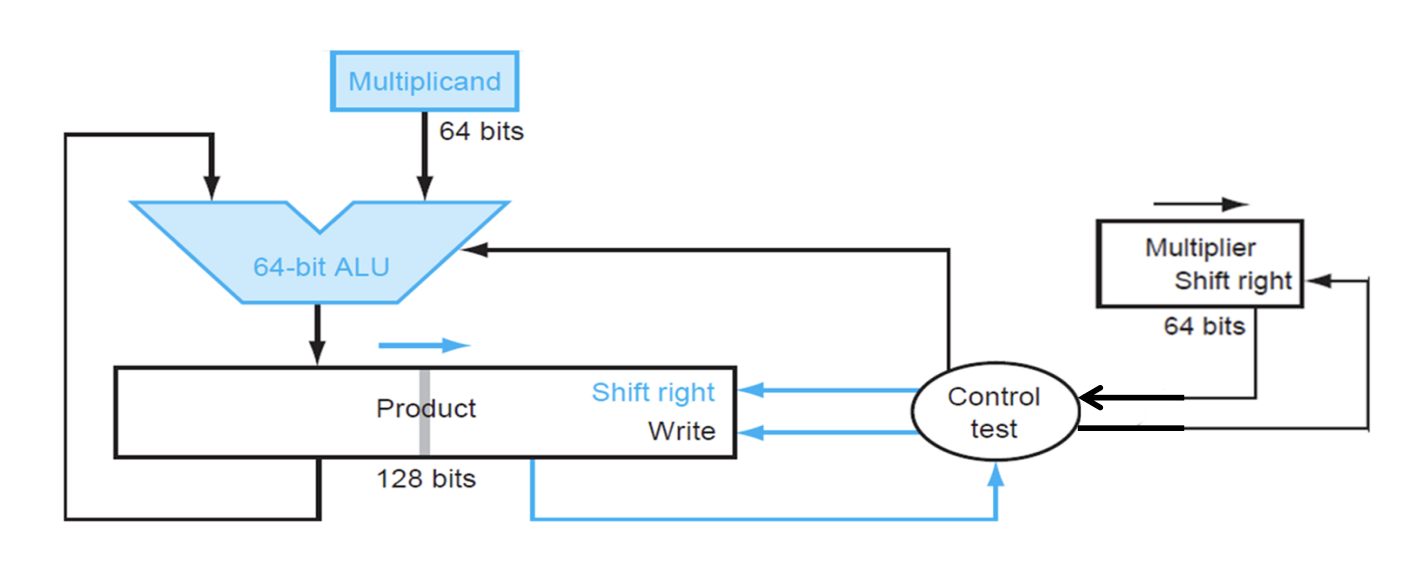
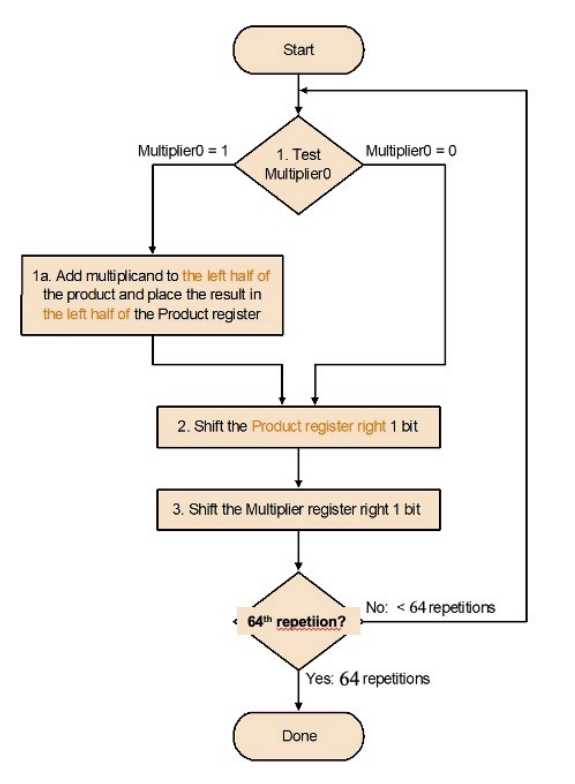
V3版本
我们继续沿着减少reg bit的使用量这一思路来进行优化
减少reg使用量的一个突破口,就是看运算过程中是否存在一个时刻,有空闲的bit
显然product一开始还有一半的bit是空闲的
而product实际参与运算部分为64bit,且product每轮右移;multiplier一开始占64bit,也每轮右移
于是我们可以将multiplier一开始就放在product的低半边
每轮开始检查product的LSB即可
又省了64bit
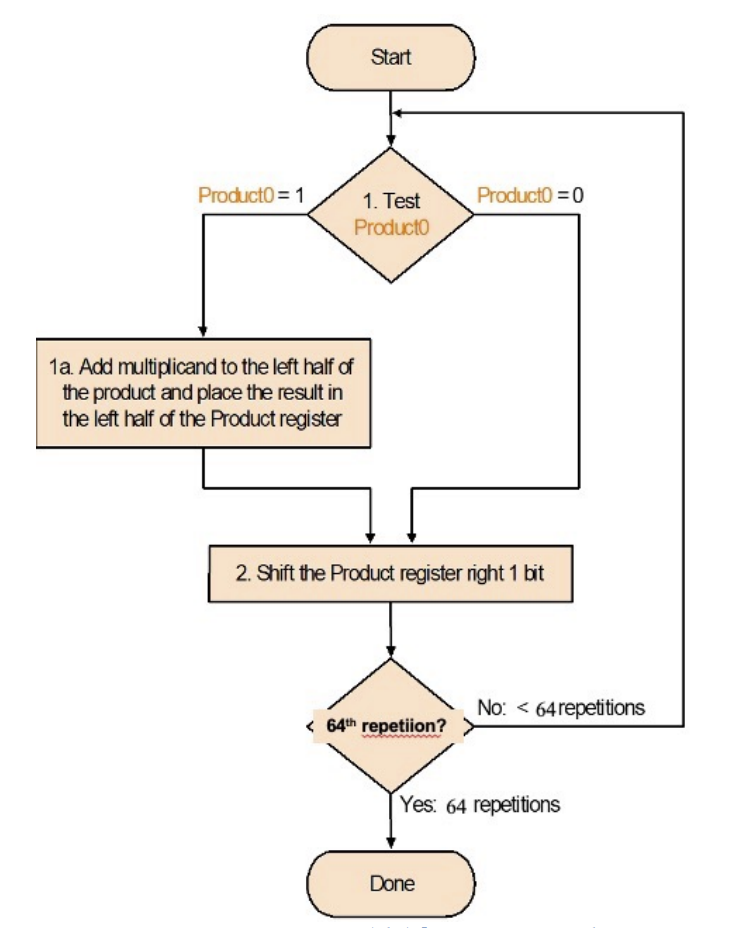
有符号数乘法
储存符号位,剩余部分当作无符号数计算,另外比较符号位得到新符号位
- 两符号位相等,结果取0
- 否则取1
Booth‘s Algorithm
乘数和被乘数1很多的话算的很复杂,因为0只需要移位,而1不仅要移位还要进行ALU加法
关注multiplier和multiplicand中==连一起==的1,将其与独立的1拆分开,并转化为独立的1
例如100111110,可以这样转化:100111110+10-10 = 100000000+1000000-10,转化成了更少的加法+一些减法+更多的移位
只要移位比加法快,这就是值得的
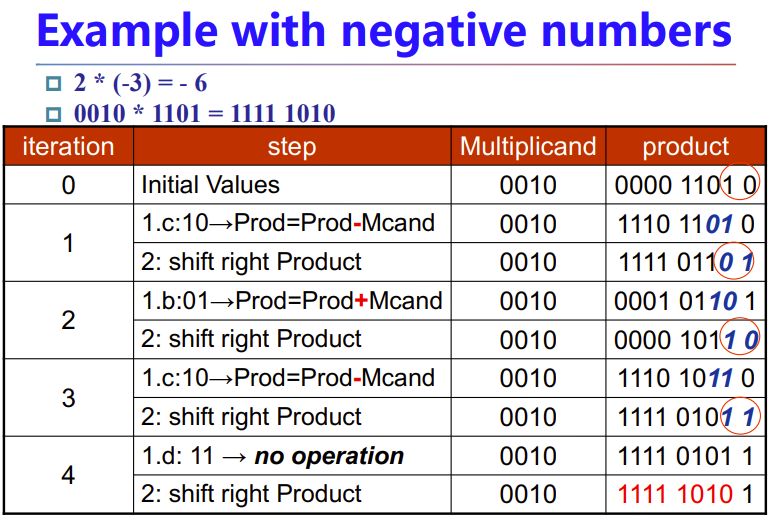
经验:布斯算法支持直接将两个有符号数当成无符号数来运算,不用管符号位。
下面两张不知道什么意思,得听智云第三周课

除法的实现
整个乘法都需要重新学一遍,完全没学
dividend:被除数
divisor:除数
quotient:商
算法
V1版本
最基础的算法就是将除法看成多次减法,大就减,小就补
- 先检查divisor是否是0,再开始迭代
- 第一轮先看divisor位数,取出位数相同的高位部分dividend,
- 不是第一轮dividend就直接用上一轮留下的bit
- 比大小
- 后者大则quotient插入1
- 否则插入0,并让dividend向后借位
上面是手算的算法,具体的V1版本看流程图
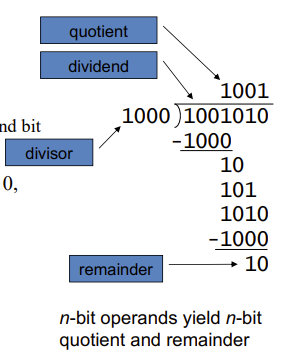

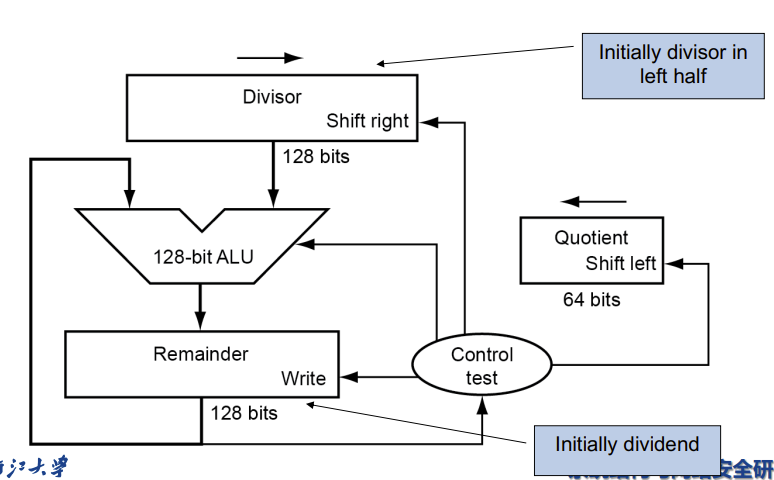
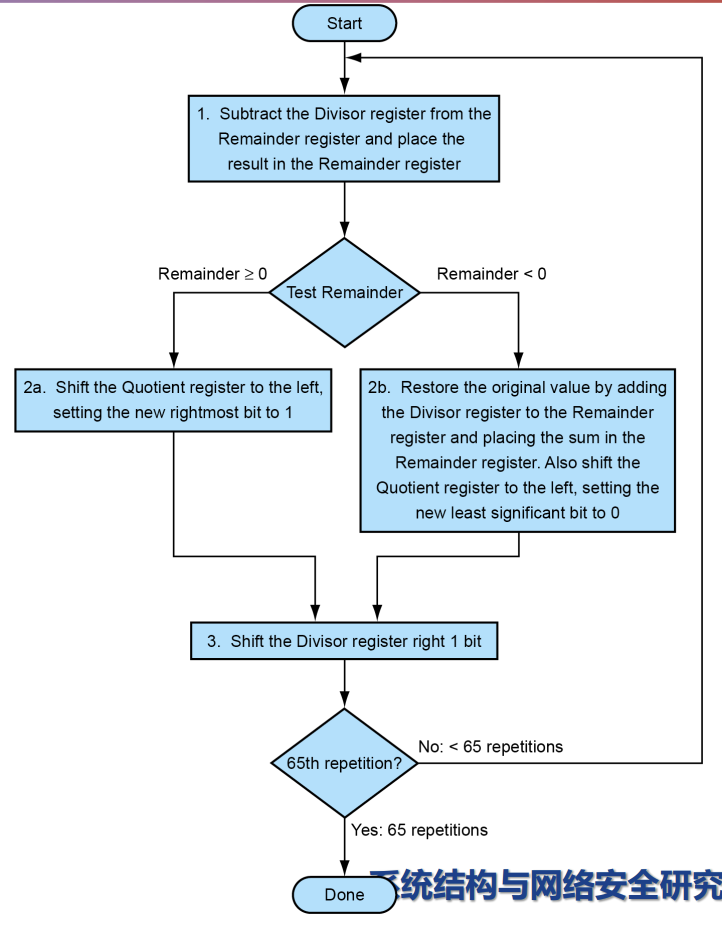
注意是迭代65轮,设计缺陷导致要多一轮
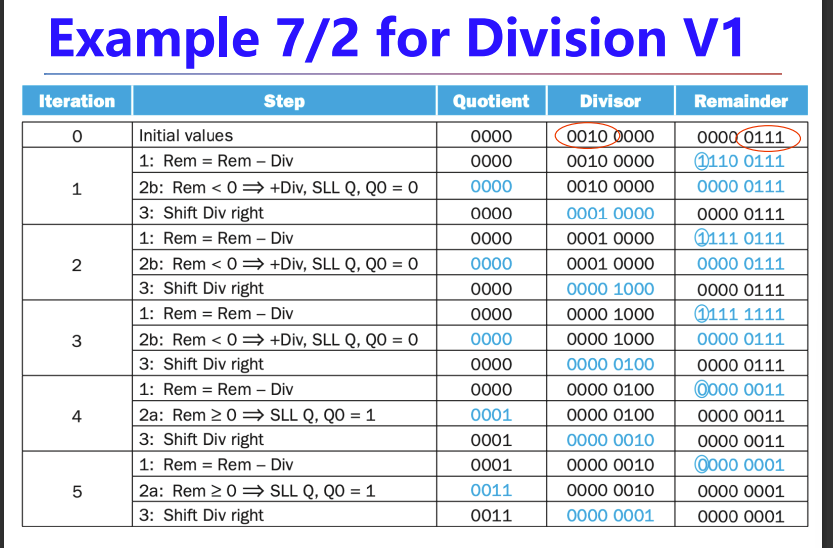
V2版本
类似乘法的优化思路:减少reg bits
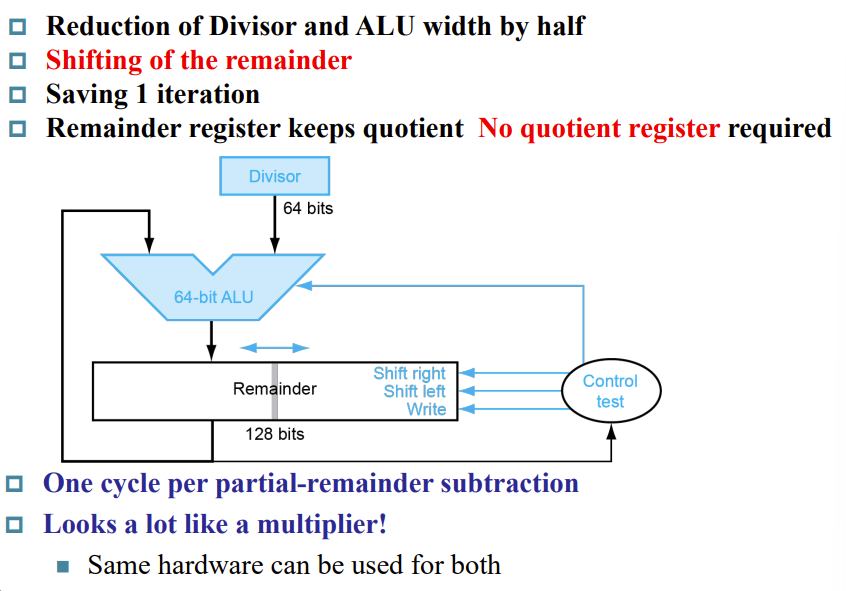
V3版本
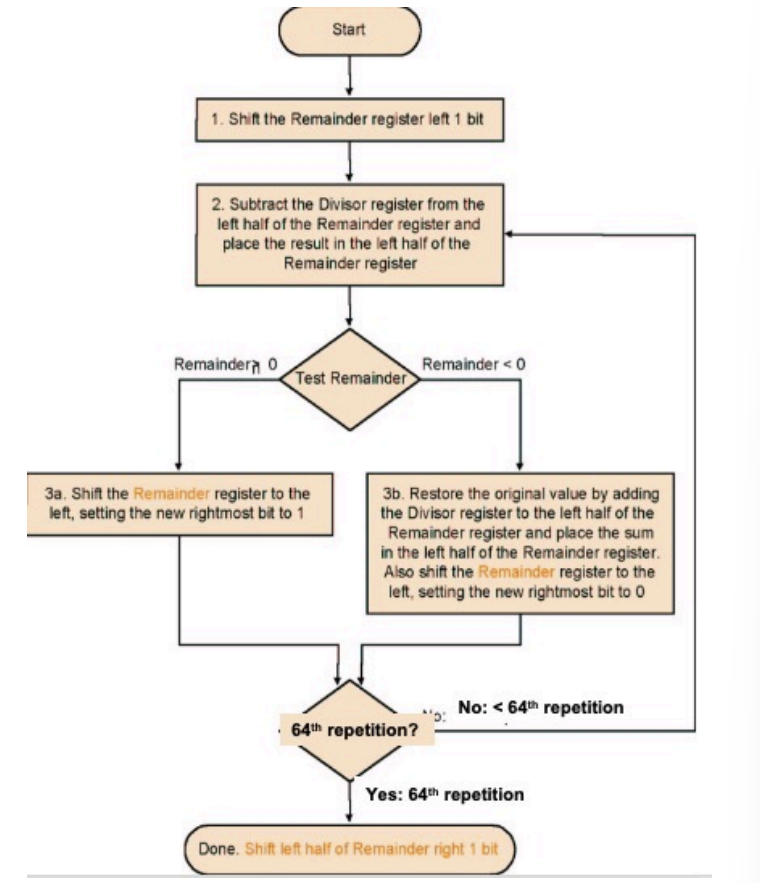
注意这里优化后不是65轮,而是64轮后再额外操作
64轮循环后,需要再对remainder的左半部分做一次右移运算,不然remainder会大2两倍
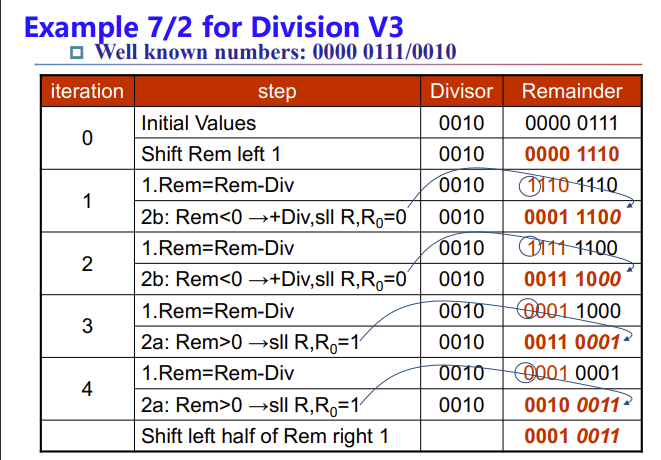
Signed division
商的符号判断和乘法一样
余数的符号跟着被除数

- 除法不能并行处理,因为 “除尽” 这件事不确定,下一位的运算依赖上一位的余数
- 可以predict一下,比如查表
- 至于除数是0的情况,可以通过软件避免,所以硬件没有涉及
- 溢出也没涉及
- common fast,没必要为了除法增加硬件
- 根据阿姆达尔定理,主要加快加法即可
上面的算法都是针对int,实际上用的更多的是浮点数
阿姆达尔定律
Gene Amdahl进行了一个富有洞察力的观察: 提升一个系统的一个部分的性能对整个系统有多大影响。这一观察被称为Amdahl's Law(阿姆达尔定律)。
(注:这里的系统,可指计算机系统或别的什么系统)
当提升系统的一部分性能时,对整个系统性能的影响取决于:1、这一部分有多重要 2、这一部分性能提升了多少。
初中数学。。。
浮点数
概念
- Form
- Arbitrary:\(363.4\cdot 10^{34}\),\(10.1011\cdot 2^{-5}\)
- Normalised:\(3.634\cdot 10^{34}\),\(1.01011\cdot 2^{-4}\)
- Normalised 后的 有效数字(如3.634) 叫做尾数(Significand)
- \(2\) 和 \(10\) 是 基数(Radix)
- 精度
- float 是 32bit
- double 就是 \(32bit \times 2\)
- \(exp\) 多 3bit
- \(fraction\) 多 32-3=29bit

-
Infinities and NaNs
- \(exp\) 全为
1,\(frac\) 全为1$\rightarrow $±Infinities,可用于检查overflow
- \(exp\) 全为
1,\(frac\) 不为 0 $\rightarrow $Not-a-Number (NaN),用于表示非法/未定义数值- 如0/0的结果就是NaN
- \(exp\) 全为
- Overflow & Underflow
- Overflow: The number is too big to be represented
- Underflow: The number is too small to be represented
IEEE 754 standard
- IEEE 754 standard
- \((-1)^{sign}\cdot (1+fraction)\cdot 2^{exp-bias}\)
- 表示的是 Normalised form
- \(fraction\) 只有小数部分,反正Normalised form整数一定是一个
1 - 实际储存的 \(exponent\) 数值需要减去 \(bias\) 才是实际的
- 储存的是实际值加上 \(bias\) ,这是为了让储存的数值一定 \(\geq 0\)
- 对于 \(float\) ,\(bias = 127\),即 \(2^{exp位数-1}-1\)
- 对于 \(double\),\(bias = 1023\),即 \(2^{exp位数-1}-1\)
- \(bias\) 就是让最小的负数变0,分别就是-127和-1023
- 十进制转 IEEE 754 standard 浮点数
- 先转化为二进制
- 再转化为二进制的 Normalised form
- 再按IEEE 754 standard 分配位值,主要注意 \(fraction\) 只有小数,\(exp\) 要加 \(bias\)
Range
- Range
- Single-Precision Range
- Exponents 00000000 and 11111111 reserved,即这两个 \(exp\) 不能用(见上文)
- Accessible Exponent:00000001 ~ 11111110
- -126 ~ 127
- Fraction:000…00 ~ 111…11
- 1.0 ~≈2.0
- Values: \(±1.0 × 2^{–126}\) ~ \(±2.0 × 2^{+127}\)
- ≈\(±1.2 × 10^{–38}\) ~ ≈\(±3.4 × 10^{+38}\)
- Exponents 00000000 and 11111111 reserved,即这两个 \(exp\) 不能用(见上文)
- Double-Precision Range
- Exponents 0000…00and 1111…11 reserved
- Accessible Exponent:-1022 ~ 1023
- \(1-1023=-1022\)
- \(2046-1023=1023\)
- Accessible Exponent:-1022 ~ 1023
- Fraction:000…00 ~ 111…11
- 1.0 ~≈2.0
- Values: \(±1.0 × 2^{–1022}\) ~ \(±2.0 × 2^{+1023}\)
- ≈\(±2.2 × 10^{–308}\) ~ ≈\(±1.8 × 10^{+308}\)
- Exponents 0000…00and 1111…11 reserved
- Single-Precision Range
- Precision
- Single: \(\approx 2^{–23}\)
- 十进制小数点后6位
- Double: \(\approx 2^{–52}\)
- 十进制小数点后16位
- Single: \(\approx 2^{–23}\)
浮点数加法
- 步骤
- Alignment
- Add Significands
- Normalize the sum
- Over/underflow
- Rounding
- Normalization
Example for Decimal

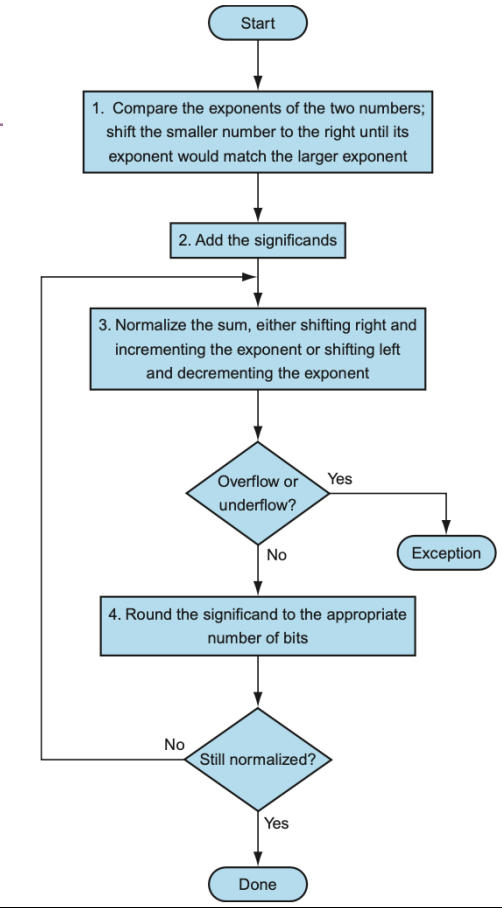
算法
- 比较exp,将小的右移,直到exp相等,完成对齐
- 移小的是为了减少数值损失
- 尾数相加
- 规范结果格式
- 检查有无溢出,有就异常退出
- round,就是去除多的位,毕竟位数固定
- 检查是否已规范,若未规范就回到第3步
- 完成!
Example

这图里的round意思不对?round是去除多的位,毕竟位数固定
电路图
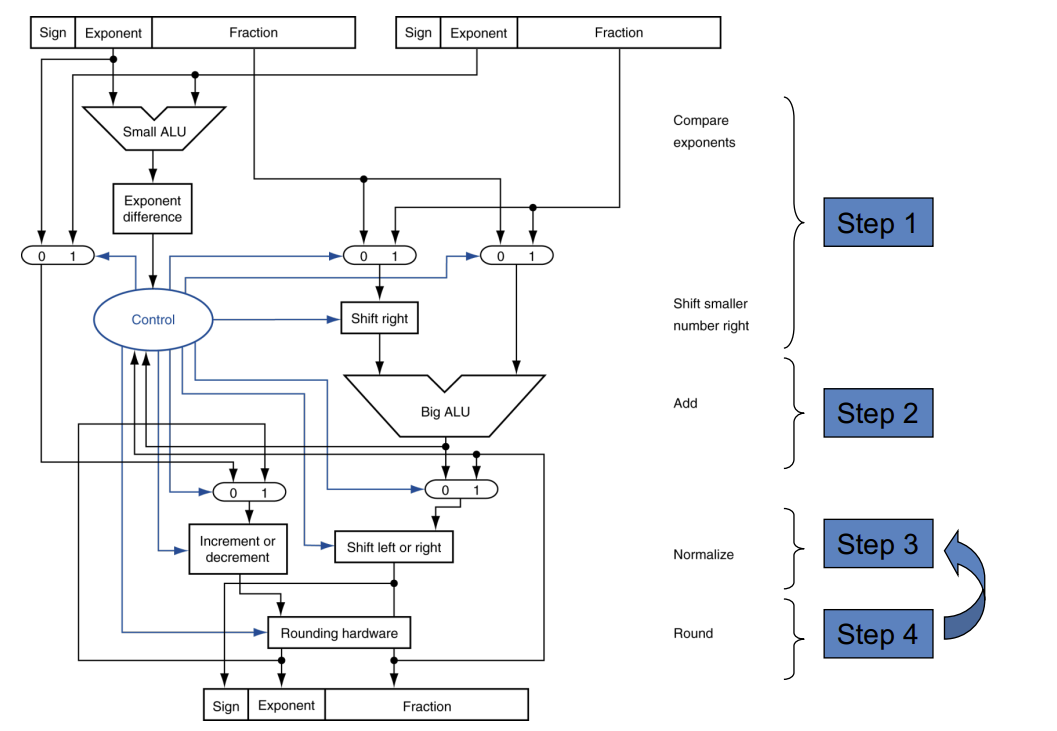
浮点数乘法
尾数与指数分别处理即可,当然还要处理符号位:
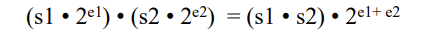
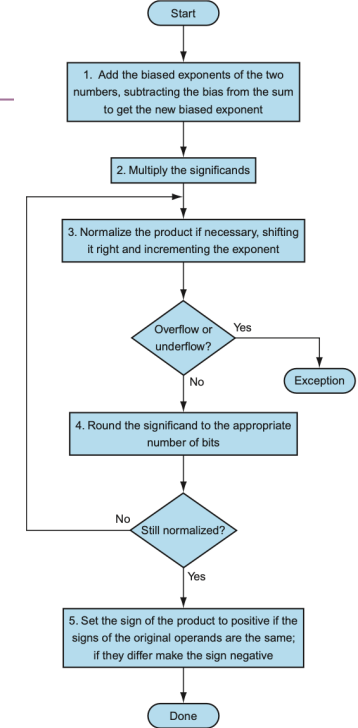
算法
- 指数相加
- 尾数相乘
- 规范化
- 检查溢出,溢出了就异常终止
- rounding
- round后检查是否规范,未规范就回到第3步
- 处理符号位
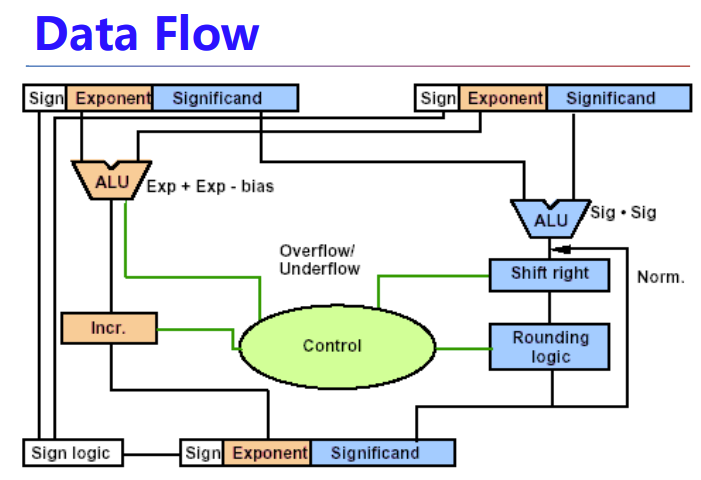
浮点数除法
和乘法一样,指数相减,尾数相除,规范化,round,符号位处理
