Lecture 2 关系数据模型
主要内容:
数据模型是数据库系统的一个根本特性。关系数据模型因为其简单有效而在数据库领域占据主导地位。讲授关系模型的数学模型,包括关系模型的数据结构、数据完整性、数据操作;重点讲授关系代数及基本关系操作及附加关系操作,学习用关系代数表达式表达数据查询要求。
我们学的重点是关系模型,图视化就是表格
这节课信息量超级巨大,需要课后再反复看一下,重新整理
Basic Structure

Relation Schema and Instance

Attributes

Relations are Unordered
Order of tuples is irrelevant (tuples may be stored in an arbitrary order)
Database Schema

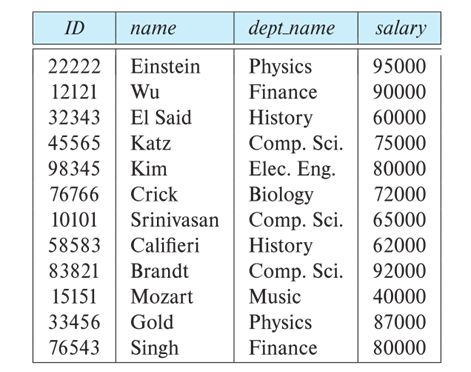
Keys

关系型数据库中的一条记录中有若干个属性,若其中某一个属性组(注意是组)能唯一标识一条记录,该属性组就可以成为一个主键
比如:
- 学生表(学号,姓名,性别,班级)
- 其中每个学生的学号是唯一的,学号就是一个主键
- 课程表(课程编号,课程名,学分)
- 其中课程编号是唯一的,课程编号就是一个主键
- 成绩表(学号,课程号,成绩)
- 成绩表中单一一个属性无法唯一标识一条记录,学号和课程号的组合才可以唯一标识一条记录,所以 学号和课程号的属性组是一个主键
成绩表中的学号不是成绩表的主键,但它和学生表中的学号相对应,并且学生表中的学号是学生表的主键,则称成绩表中的学号是学生表的外键
即,A是R1的主键,但在R2里不是主键,那么R2里的A是R1的外键
同理 成绩表中的课程号是课程表的外键
定义主键和外键主要是为了维护关系数据库的完整性,总结一下:
- 主键是能确定一条记录的唯一标识,比如,一条记录包括身份正号,姓名,年龄。
身份证号是唯一能确定你这个人的,其他都可能有重复,所以,身份证号是主键。
- 外键用于与另一张表的关联。是能确定另一张表记录的字段,用于保持数据的一致性。
比如,A表中的一个字段,是B表的主键,那他就可以是A表的外键。
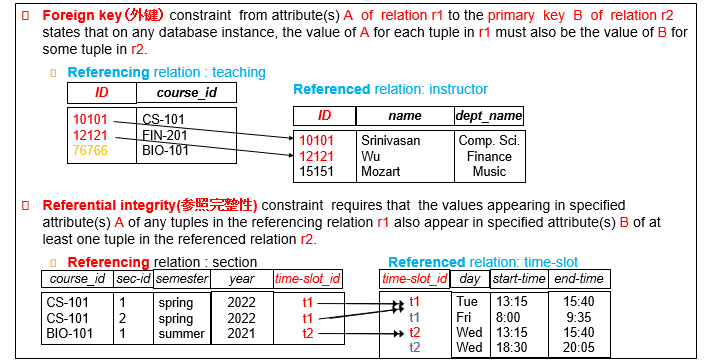
实体完整性
保证关系中的每个元组都是可识别的和惟一的
指关系数据库中所有的表都必须有主键,而且表中不允许存在如下记录: – 无主键值的记录 – 主键值相同的记录 原因:实体必须可区分
参照完整性
也称为引用完整性
现实世界中的实体之间往往存在着某种联系,在关系模型中,实体以及实体之间的联系都是用关系来表示的,这样就自然存在着关系与关系之间的引用
参照完整性就是描述实体之间的联系的
参照完整性一般是指多个实体或关系之间的关联关系
此完整性涉及到了外键:
- 参照完整性规则就是定义外键与被参照的主键之间的引用规则
- 外键一般应符合如下要求:
– 或者值为空 – 或者等于其所参照的关系中的某个元组的主键值
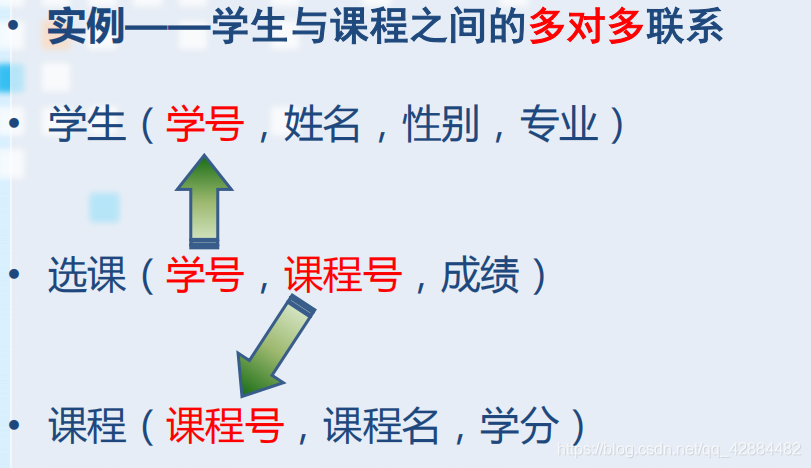
Database

Relational Algebra

Basic Operation
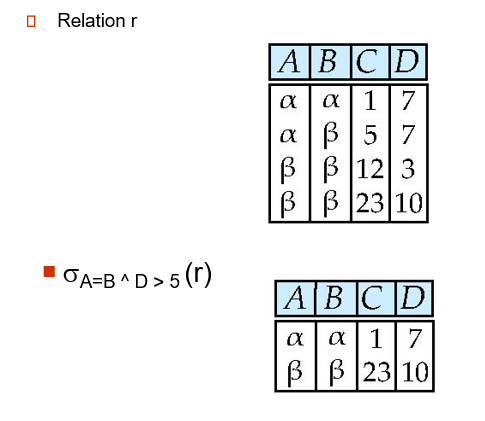
Select Operation
横向选择

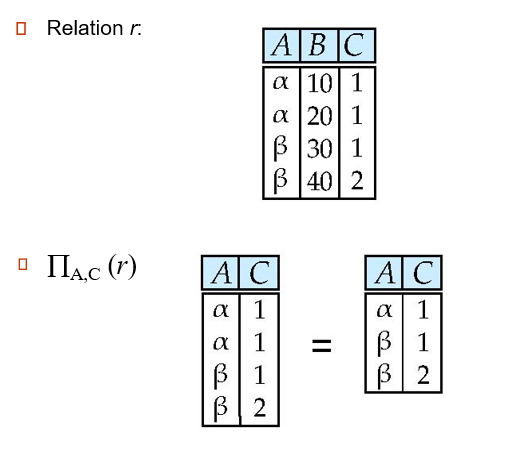
Project Operation
纵向选择

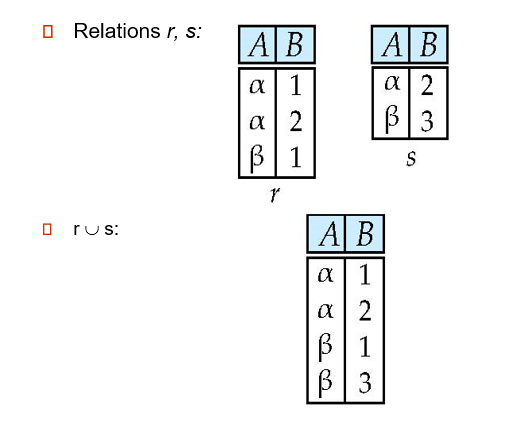
Union Operation

不能乱并,得相容
Set difference

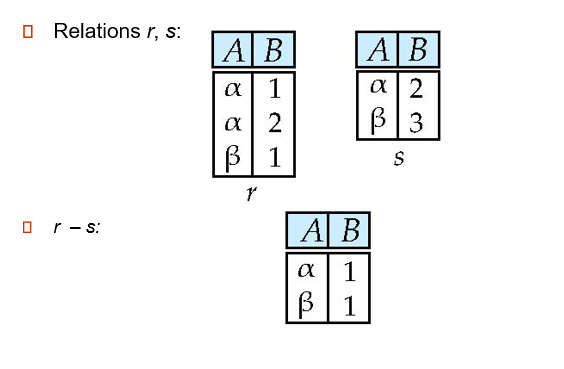
交集可以用此操作体现,r^s = r-(r-s)
Cartesian-Product Operation


Rename Operation

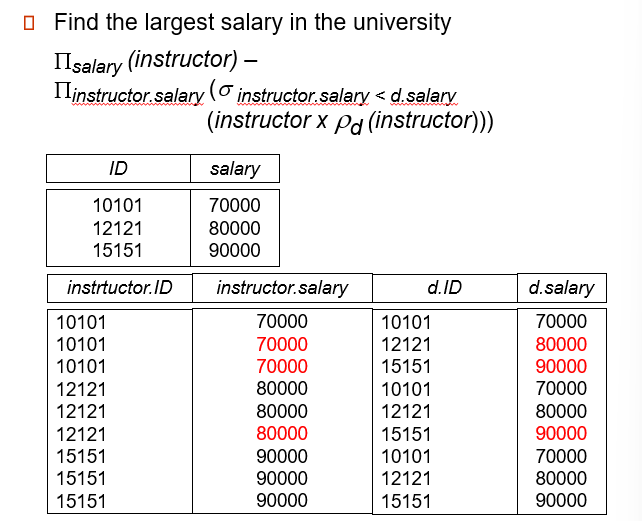
Example Queries

显然第二种效率更高,中间量少很多,这属于夏学期的优化问题
不过很多语句DBMS会自动优化


不是所有的想法都能用关系代数实现
Formal Definition

Additional Operations

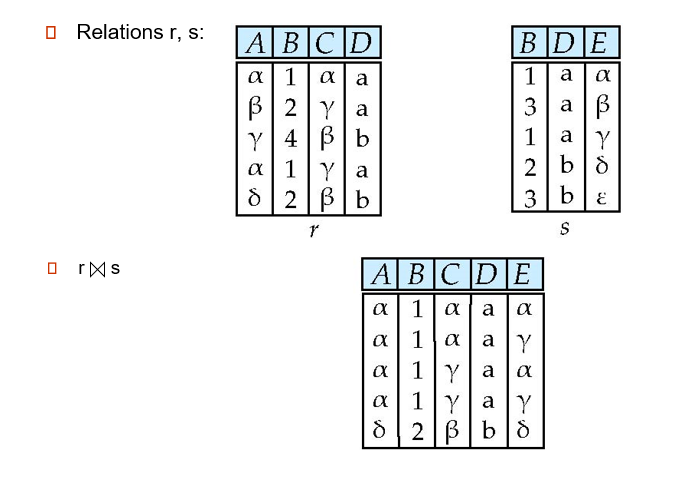
Natural-Join Operation


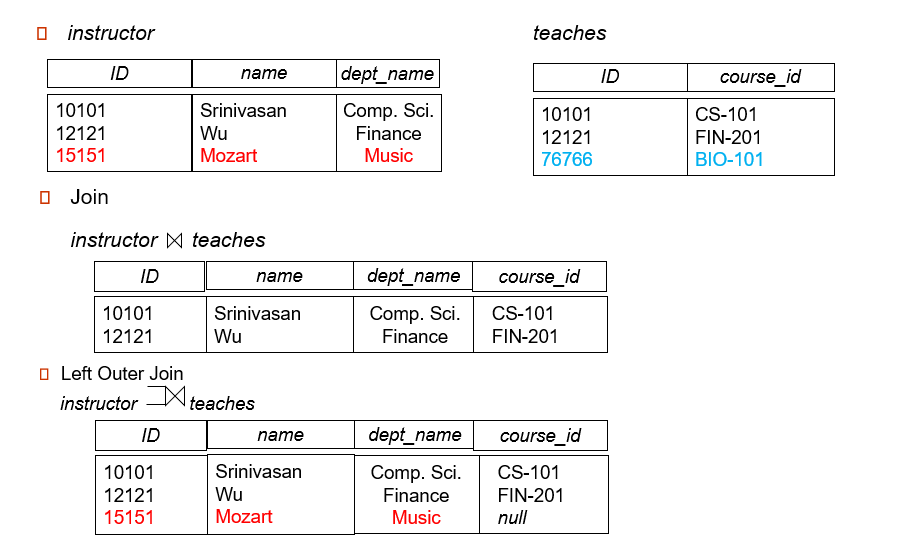
Outer Join

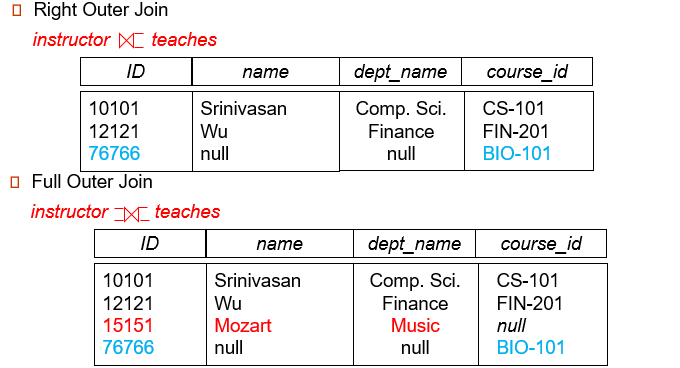

花括号表示临时构造一个关系,圆括号表示一个元组
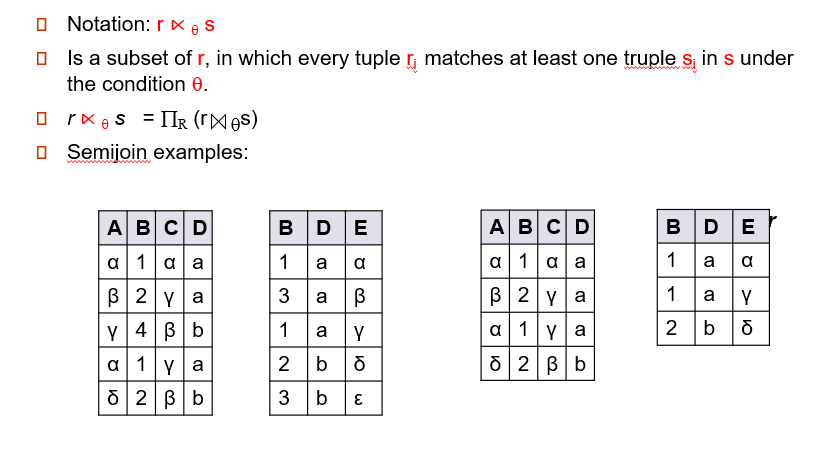
Semijoin(半连接) Operation
没听懂,15:14

Null Values

Assignment Operation

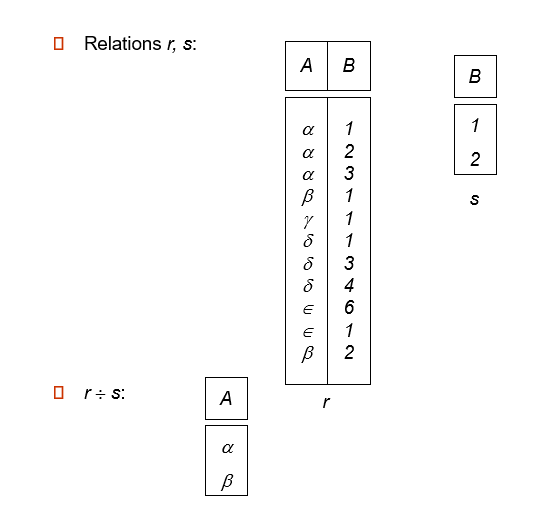
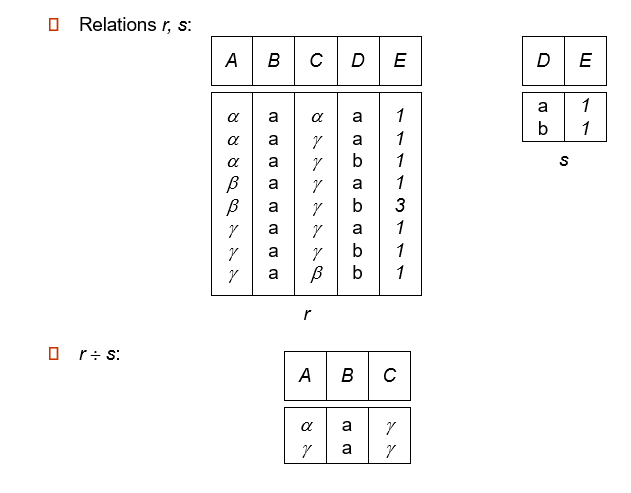
Division Operator
就是看r-s中的tuple,如果一个r-s的tuple在r中所处的tuple包含了所有s中的tuple,那它就是满足条件的结果之一

Extended Relational-Algebra-Operations
后面懒得看了,之后再看
上面的addition都没有增强查询功能,只是简化一些,接下来的就是能增强的
Generalized Projection

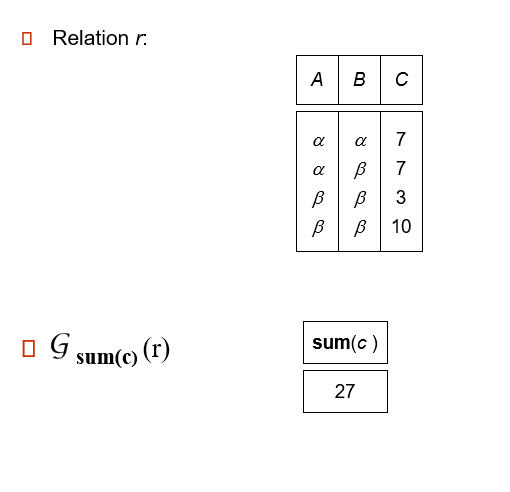
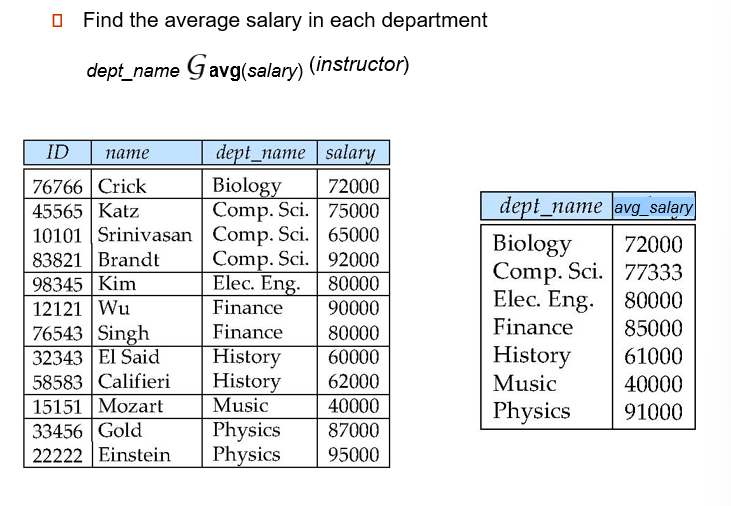
Aggregate Functions and Operations


Modification of the Database

Multiset Relational Algebra

SQL and Relational Algebra


1、不能。因为目前的关系只能直接地获取某个特定课程的上一级预修课,而关系代数只支持有限次的操作,如果没有预修课级数限制可能会出现无穷情况,这是无法实现查询的。
2、设需要查询的课程的ID为myID,则: $$ prereqA\leftarrow \Pi_{prereq_id}( \sigma_{coures_id=myID}(prereq))\ prereqB\leftarrow \Pi_{prereq_id}( \sigma_{coures_id=prereqA.coures_i}(prereq\times prereqA))\ prereqC\leftarrow \Pi_{prereq_id}( \sigma_{coures_id=prereqB.coures_i}(prereq\times prereqB))\ allPrereqOfmyID\leftarrow prereqA\cup prereqB\cup prereqC $$