Lecture 7 关系数据库设计和关系规范化
主要内容:
一个不好的关系数据模式会产生数据冗余、数据更新异常等问题。通过函数依赖的概念分析关系模式的规范化程度,并把不规范的关系模式分解为规范化的关系模式。讲授函数依赖的概念、Armstrong公理系统、关系模式的候选关键字(candidate key)以及关系模式分解的原则,即无损连接的分解和保持函数依赖的分解。
BCNF是函数依赖范畴内规范化程度最高的关系模式,而3NF是比BCNF低的规范化形式。一个关系模式总能无损连接地分解为BCNF 的关系模式,但不一定能保持函数依赖;若要求分解既是无损连接的又是保持函数依赖的,则保证可以分解为3NF。 通过考察多值依赖,还可以获得更高规范化的关系模式,即4NF。讲授函数依赖的相关概念 ,以及3NF和BCF的定义、分解为BCNF和3NF的算法;介绍多值依赖及4NF的概念。
本节课体现关系模型的理论优势
Lossless-join Decomposition
好的关系模式需要保只有key可以唯一确认一条tuple,不能有其它相同地位的attribute
而且schema尽量小一些,这样表也能小很多
但是我们需要关注的是,拆分后的schema与原来的schema是否有数据变化
例如将下面的关系拆分为两个schema
inst_dept(id,name,salary,dept_name, building, budget)
->teacher(id,name,salary,dept_name)
->dept(dept_name, building, budget)
需要进行 自然连接 才能无损恢复,但也属于无损拆分
First Normal Form
表中无表,即每个属性都是不可分割的。
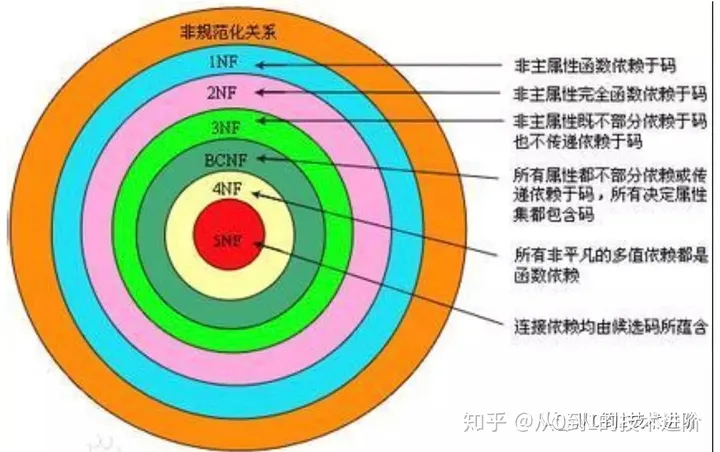
A relational schema R is in first normal form if the domains of all attributes of R are atomic
Domain is atomic if its elements are considered to be indivisible units
Examples of non-atomic domains:
Set of names, composite attribute
Identification numbers like CS101 that can be broken up into parts
- Normal Forms(NF):
- 1NF
- 表中无表,即每个属性都是不可分割的。
- 不满足第一范式的数据库就不是关系型数据库,所以说能在MySql建立的表肯定满足第一范式。
- 2NF
- 满足第一范式基础上,非主属性必须完全依赖于主属性。
- 即主键的整体才能确定一个非主属性。
- 如果主键的部分属性就确定了一个非主属性就不满足第二范式。 1. 例如,一个表为 R (学号,课程号,成绩,姓名, 老师,老师职称) 2. 我们现在要新增一个学生,该学生还没有选课,因此就不能新增。课程号是关键码,又必须添加,产生了冲突。这是因为知道学号,姓名就确定一个学生,并不需要课程号。 3. 这个R就不是第二范式
- 3NF
- BCNF
- 4NF
- 1NF
一个关系模式,如果只有key能够决定所有的属性,就达到了BCNF
确认一个关系模式好坏的具体理论,包括:
- functional dependencies
- multivalued dependencies
Functional Dependencies
函数依赖
什么是函数依赖

就是属性\(\alpha \(的value确定了,\)\beta\)也就确定了。两个tuple的\(\alpha\)相同,那么\(\beta\)也一定相同
如两个表里,同一个学号一定对应同一个姓名
key就是函数依赖的特殊情况,函数依赖是普遍存在的

但是有一种没有任何意义的、普遍存在的函数关系我们就称为trivial,我们一般不考虑这玩意儿

Closure(闭包)
of a Set of Functional Dependencies
一个关系模式里面,有重叠的函数依赖可以推出新的函数依赖。
函数依赖——包含被推导出的函数依赖中,所有 同一个起点的 的集合,就是这个起点的 闭包。

下面有三条公理用于推演F+的成员

自反律就是刚刚的trivial
第二个\(\gamma \alpha\)是并在一起的意思
推演例子(简单)

由公理可推导更多的定理

练习1
看一下,不会做,别看答案

of Attribute Sets
就能通过关系依赖被A决定的属性,包括A本身,组成的集合就是A的闭包
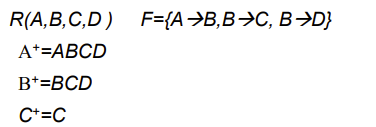
和上面的区别就是集合元素变成了属性,简洁很多
获取属性闭包的算法

其实画 单向图(Graph)就行了

Canonical Cover(正则覆盖)
怎么求??
刚刚说的闭包是尽可能列出所有的即便会重叠的函数依赖
正则覆盖则反过来化简,类似线性代数基的概念,在函数依赖中找到最小的、但是却可以确定所有函数依赖的集合

下面是具体定义:

注意要求左式只能为单
Exercise 2

Boyce-Codd Normal Form
之前也说了就是只有一个key
用函数依赖来定义就是,这个关系模式所有的函数依赖,要不是左边是key的,要不就是trivial(频繁)的
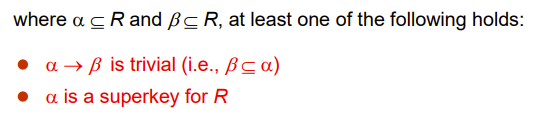
BCNF是数据库设计的基本目标
Decomposing a Schema into BCNF
分解必须是无解的
分解算法

就是,如果目前的result里面有非BCNF的,就在这个schema里面找一个函数依赖\(\alpha \rightarrow \beta\),它的左边$\alpha $不是key
然后将这个schema分为两个新的schema,一个只包含\(\alpha\)和\(\beta \(,一个去掉\)\beta\),但不去掉\(\alpha\),作为公共属性。前者的key正好是\(\alpha\)
Exercise 3

Dependency Preservation(依赖保持)
原来每一条函数依赖都能在被分解后的任意一个表上得到验证,那么就称这个分解是满足依赖保持的
注意是单独的在每一个表里面能够检验所有的依赖保持

Exercise 4

Third Normal Form: Motivation
满足第二范式基础,且消除对主属性的传递依赖。
有一张表 R (学号,课程号,成绩,姓名, 老师,老师职称)
我们可以发现(学号,课程号)之所以能决定教师职称并不是直接得出来的,是因为我们先由此推出老师是谁,才知道教师职称。
即X(学号,课程号)→Y(教师),Y(教师)→Z (教师职称) 导致的X(学号,课程号)→Z(教师职称)。
我们称教师职称是传递依赖于(学号,课程号)。
存在传递依赖也有弊端,比如:
老师职称改变了,要修改很多条数据。(修改异常)
没人选某个老师的课时候,该老师的职称记录就会被全部删除。(删除异常)
新来老师还没有定教哪门课,教师职称不知该保存到什么地方。(插入异常)
所以,我们必须消除传递依赖。具体做法就是消除传递依赖的非主属性:
(学号,课程号,成绩,教师)
(教师,教师职称)
任何一条函数依赖,要么是频繁的,要么左边是key,要么右边的属性包含在某个candidate key里面
?
显然是BCNF弱化的版本,多了个右边的性质
