图

:material-circle-edit-outline: 约 960 个字 :fontawesome-solid-code: 41 行代码 :material-clock-time-two-outline: 预计阅读时间 4 分钟

图（Graph）

图表示多对多的关系

包含：

顶点 \(V\)（Vertex）
边 \(E\) （Edge）：用顶点对 \((v,w)\) ，有向边表示为 \(<v,w>:v\rightarrow w\)
不考虑重边和自回路

完全图即最大边数情况

抽象数据类型定义

类型名称：图

数据对象集： \(G(V,E)\) 由非空有限顶点集合 \(V\) 和有限边集合 \(E\) 组成

typedef int Vertex;
typedef int WeightType;
typedef char DataType;

//Node of Edge
typedef struct ENode *PtrToENode;
struct ENode{
    Vertex V1, V2;
    WeightType Weight;
};
typedef PtrToENode Edge;

//Node of Graph
typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv; //num of vertex
    int Ne; //num of edge;
    WeightType G[MaxVertexNum][MaxVertexNum];
    DataType data[MaxVertexNum];    //ignore it if with no data
}

typedef PtrToGNode MGraph;  //matrix

操作集：

Create

MGraph Create(int Vnum){
    Vertex V,W;
    MGraph G;
    G = (MGraph)malloc(sizeof(struct GNode));
    G->Nv = Vnum;
    G->Ne = 0;
    for(V=0;V<G->Nv;V++)
        for(W=0;W<G->Nv;W++)
            G->G[V][W] = INFINTY;
   return G;
}

InsertVertex

MGraph InsertVertex(Graph G, Vertex v){
    ...    
}

InsertEdge

void InsertEdge(MGraph G, Edge E){
    G->G[E->V1][E->V2] = E->Weight;
    G->G[E->V2][E->V1] = E->Weight;
}

DFS（深度优先遍历）

void DFS(Graph G, Vertex v);

BFS（宽度优先遍历）

void BFS(Graph G, Vertex v);

ShortestPath（最短路径）

void ShortestPath(Graph G, Vertex v, int Dist[]);

MST（最小生成树）

void MST(Graph G);

图的表示

邻接矩阵 (Adjacency Matrixs)

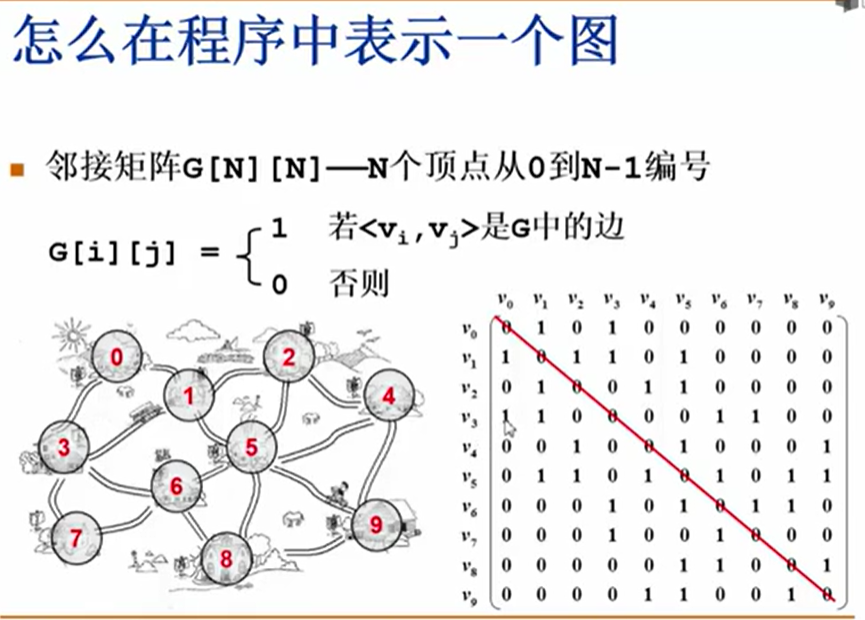
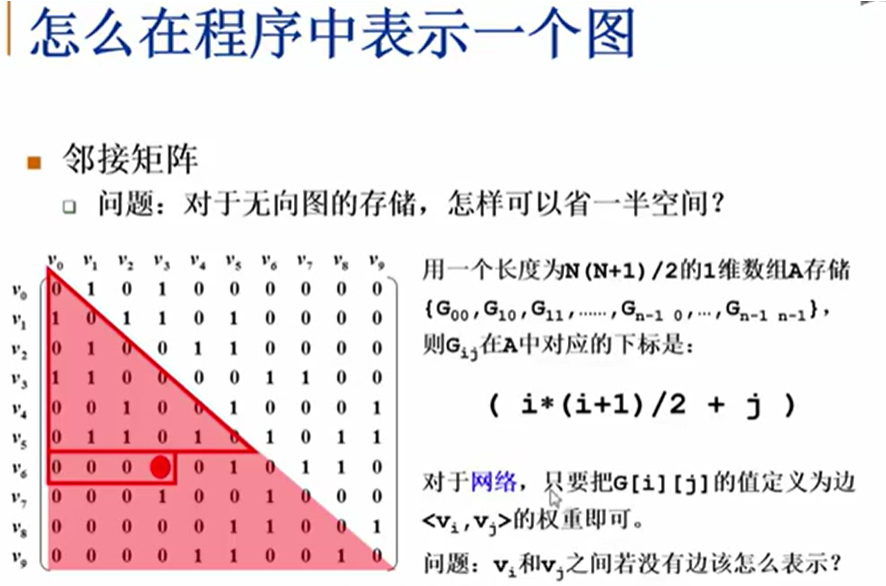
入度：指向该结点的边数
出度：从该结点出发的边数

对于有向图，行对应出度，列对应入度

邻接表 (Adjacency Lists)

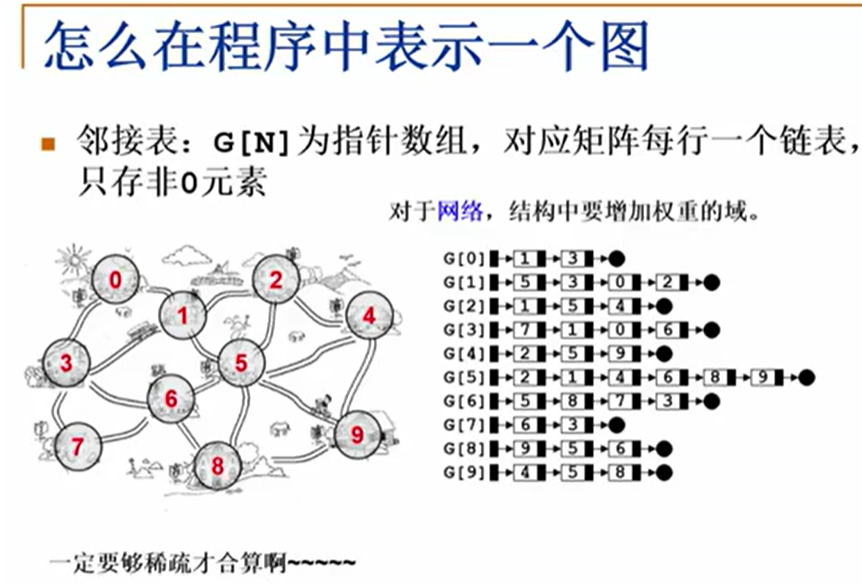
图的遍历

DFS（Depth First Search，深度优先搜索）

引入

这是一个迷宫，每个拐角有一盏灯，给了一个起点，需要去点亮每一盏灯。

先一条路走，一个一个点亮；每点亮一盏灯就检查周围的灯；若有没点亮的，就选择一个去点亮；若都点亮了，则原路返回；返回的路上也要依次再次检查。

复杂度

邻接表

考虑最坏情况，则每个节点对应N次，所有节点需要遍历E次，故 \(O(N+E)\)

邻接矩阵

考虑最坏情况，\(O(N^2)\)

BFS（Breadth First Search，广度优先算法）

类似Tree的level遍历

连通

两结点存在联通的路径即称为连通的。

路径长度：边数/权重和。
简单路径：路径经过的所有顶点均不同。
回路：起点终点一致。
连通图：图中顶点均连通。
连通分量：无向图的极大连通子图
- 极大顶点数：再加1个顶点就不连通了
- 极大边数

强连通

强连通：两顶点间存在双向路径
强连通图
强连通分量
- 对于一个孤立的顶点，可认为其本身是强连通的

最短路径问题（Shortest Path）

路径第一个顶点为源点（Source）

对后一个顶点为终点（Destination）

单源无权图

思路：按照递增顺序一个一个标记。利用BFS实现。

dist[W]= S到W的距离，dist[S] = 0
path[W]= S到W路上，W的上一个顶点V

两者一般初始化为-1，dist[W]==-1 表示W未访问过

复杂度

\(T=O(V+E)\)，访问了2V和1E

具体思路

类似BFS。

使用一个队列。首先压入源点。
弹出V，同时准备压入V指向的每个邻接点W。
对于每一个W，压入前需要检查是否被访问过（dist[W]==-1）。
压入后更新dist（dist[W]=dist[V]+1），更新path（path[W] = V）。

如此循环。

单源有权图

不讨论权值为负的情况

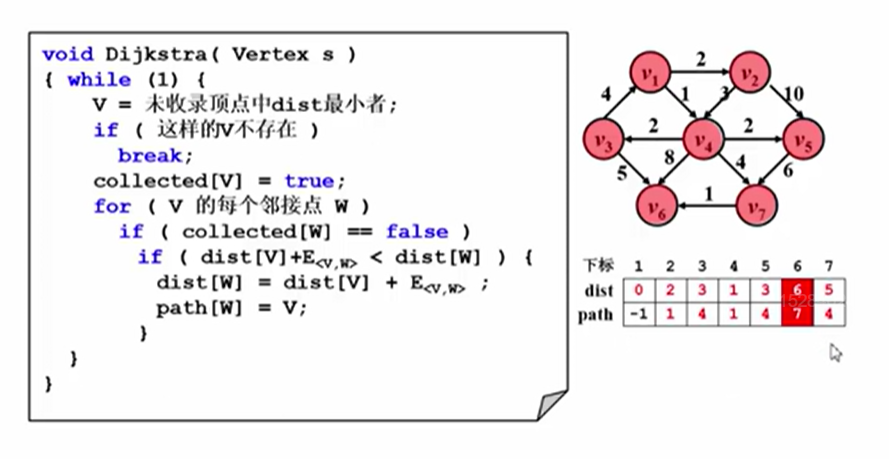
Dijkstra算法

思路和无权图类似，按递增顺序一个一个标记。

无法解决负值情况。

S：包含源点和所有确定了最短路径的顶点v
dist：对于未收录于S的顶点V，dist表示源点到V的暂时的最短路径——仅经过S目前所包含的顶点。
- dist 初始化为 infinity

每次从未收录的顶点中选一个dist最小的收录（贪心算法思想）

dist[W] = min{dist[W], dist[V]+<v,w>（权值）}

复杂度

这个问题不科学，取决于如何寻找未收录的顶点中选一个dist最小的

直接扫描所有未收录顶点（\(O(V)\)）：\(T=O(V^2+E)\)，对于稠密图效果好
将dist存储在最小堆（\(O(logV)\)）：\(T=O(VlogV+ElogV) = T(ElogV)\)，对于稀疏图效果好
1. 等式是因为一般边多于顶点

多源最短路

直接将单源算法重复调用： \(T=O(V^3+EV)\)，适合稀疏图
Floyd算法：\(T=O(V^3)\)

图