树
基本术语
- Degree of Node: number of child of a node
- Degree of Tree: max number of degree of node
- leaf: the node that degree = 0, namely, without child
- parent: namely
- sibling: the node that has the same parent
- ancestor: 沿着root到某node路上的所有node都是该node的ancestor
- descendant: 某node的child的所有node都是descendant
- level of node: root是level-1,依次往下增加层数
- depth of tree: max level
二叉树(binary tree)
分类
- 斜二叉树 skewed binary tree:全都只有左child或全都只有右child
- 完美二叉树/满二叉树 perfect binary tree/full binary tree
- depth = k && node = \(2^{k-1}\)
- 完全二叉树 complete binary tree/CBT
性质
- level = \(i\) -->
max number of node in this level= \(2^{i-1}\) - depth = k -->
max number of node in this tree= \(2^{k-1}\) number of leaf= \(n_0\) ,number of node with degree 2= \(n_2\) --> \(n_0 = n_2+1\)- \(n_2+n_1+n_0=0*n_0+1*n_1+2*n_2+1\)
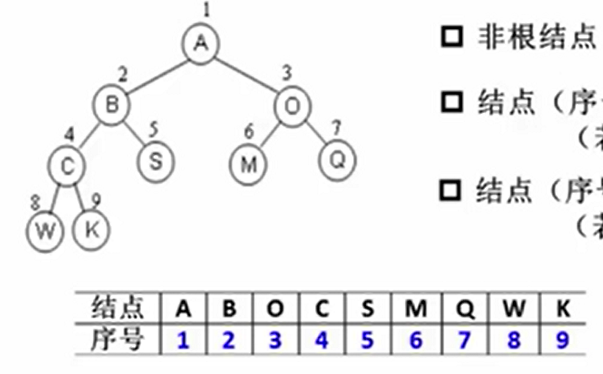
普通树转二叉树
- 将树的根节点直接作为二叉树的根节点
- 将树的根节点的第一个子节点作为根节点的左儿子,若该子节点存在兄弟节点,则将该子节点的第一个兄弟节点(方向从左往右)作为该子节点的右儿子
- 将树中的剩余节点按照上一步的方式,依序添加到二叉树中,直到树中所有的节点都在二叉树中
遍历
typedef struct TNode *Position;
typedef Position BinTree; /* 二叉树类型 */
struct TNode{ /* 树结点定义 */
ElementType Data; /* 结点数据 */
BinTree Left; /* 指向左子树 */
BinTree Right; /* 指向右子树 */
};
void PreorderTraversal( BinTree BT )
{
if( BT ) {
printf("%d ", BT->Data );
PreorderTraversal( BT->Left );
PreorderTraversal( BT->Right );
}
}
void InorderTraversal( BinTree BT )
{
if( BT ) {
InorderTraversal( BT->Left );
/* 此处假设对BT结点的访问就是打印数据 */
printf("%d ", BT->Data); /* 假设数据为整型 */
InorderTraversal( BT->Right );
}
}
void PostorderTraversal( BinTree BT )
{
if( BT ) {
PostorderTraversal( BT->Left );
PostorderTraversal( BT->Right );
printf("%d ", BT->Data);
}
}
void LevelorderTraversal ( BinTree BT )
{
Queue Q;
BinTree T;
if ( !BT ) return; /* 若是空树则直接返回 */
Q = CreatQueue(); /* 创建空队列Q */
AddQ( Q, BT );
while ( !IsEmpty(Q) ) {
T = DeleteQ( Q );
printf("%d ", T->Data); /* 访问取出队列的结点 */
if ( T->Left ) AddQ( Q, T->Left );
if ( T->Right ) AddQ( Q, T->Right );
}
}
存储结构
顺序存储
- 一般用完全二叉树
- 对于第 \(i\) 个节点: \(parent = i/2,\;leftChild=2i,\;rightChild = 2i+1\)
链表存储
typedef struct TreeNode *BinTree;
type BinTree Position;
struct TreeNode{
int data;
BinTree Left;
BinTree Right;
}
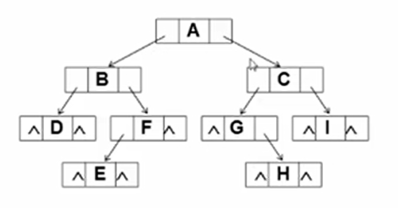
threaded binary trees
每个结点都有两个指针用于指向child,但是有些结点degree不是2,即有NULL空指针。
而且我们发现遍历比较麻烦,如果能记住某种遍历的先后顺序就能大大节省时间。
于是我们利用上这些空指针。
将所有的空指针域中的lchild,改为指向它的前驱结点,即某种遍历下该结点的上一个结点。
下图为中序遍历的前驱指针示意。
将所有的空指针域中的rchild,改为指向它的后继结点,即某种遍历下该结点的上一个结点。
下图为中序遍历的后继指针示意。
二叉搜索树(Binary Search Tree/BST)
又称二叉排序树/二叉查找树
对与任意Node,其左子树所有键值均小于其,其右子树所有键值均大于其
显然,其子树均为BST
操作
Find
递归版
Position Find(int X,BinTree BST){
if(!BST) return NULL;
if(X>BST->data) return Find(X,BST->Right);
else if(X<BST->data) return Find(X,BST->Left);
else return BST;
}
迭代版
Position Find(int X,BinTree BST){
while(BST){
if(X>BST->data) BST = BST->Right;
else if(X<BST->data) BST = BST->Left;
else return BST;
}
return NULL;
}
非递归函数执行效率更高
Insert
BinTree Insert(int X, BinTree BST){
if(!BST){
BST = (BinTree)malloc(sizeof(struct TreeNode));
BST->data = X;
BST->Left = BST->Right = NULL;
}else
if(X<BST->data)
BST->Left = Insert(X,BST->Left);
else if(X>BST->data)
BST->Right = Insert(X,BST->Right);
return BST;
}
Delete
思路:用右子树最小元素或左子树最大元素替代被删除元素。下面代码默认用前者。
BinTree Delete(int X, BinTree BST){
Position tmp;
if(!BST) return;
else if(X<BST->data)
BST->Left = Delete(X,BST->Left);
else if(X>BST->data)
BST->Right = Delete(X,BST->Right);
else
if(BST->Left && BST->Right){
tmp = FindMin(BST->Right);
BST->data = tmp->data;
BST->Right = Delete(BST->data,BST->Right);
}else{
tmp = BST;
if(!BST->Left)
BST = BST->Right;
else if(!BST->Right)
BST = BST->Left;
free(tmp);
}
return BST;
}
平衡二叉树(balanced Binary Tree/AVL Tree)
平衡因子(Balanced Factor/BF)
\(BF(T) = h_L-h_R\), 即左右子树高度之差
高度 = 深度 - 1
AVL树首先,是二叉搜索树;其次,要求 \(\lvert BF\rvert \le1\)
常用结论:最少节点数


调整
构造AVL树的方法就是在搜索树的
insert函数里,每输入一个数值就进行检查与调整
RR旋转/右单旋
RR指离插入点最近的第一个平衡的节点(A)的右孩子(B)的右子树(BR),RR插入时需要RR旋转

LL旋转/左单旋
LL同理

LR旋转
LR同理,左孩子的右子树

RL旋转
同理

堆(Heap)
优先队列(Priority Queue)
一种特殊的队列。每个元素有优先权/关键字,取出元素的顺序是依照元素的优先权大小决定的。
PQ的CBT表示即最大堆和最小堆。
堆的特性
- 结构性:用Array表示的CBT
- 有序性:任意结点的关键字是其子树所有结点的最值
- 最大值则为 最大堆(MaxHeap)
- 最小值则为 最小堆(MinHeap)
- Array的第0个地址不存放
以下以最大堆为例介绍堆
抽象数据类型表述
类型名称:最大堆
数据对象集:CBT,且每个结点的元素值不小于其结点
操作集:
Creat
MaxHeap Creat(int MaxSize){
MaxHeap H = (struct HeapStruct)malloc( sizeof(struct HeapStruct) );
H->data = (int)malloc( (MaxSize+1) * sizeof(int) );
H->size = 0;
H->capacity = MaxSize;
H->data[0] = MaxData; //作为哨兵(sentinel),MaxData设置为无限大的数
return H; //注意,root不是哨兵,哨兵在root的上面。
}
Empty
Full
Insert
注意,按照CBT格式完成插入。哨兵避免了一些bug。
void Insert(MaxHeap H, int item){
int i;
if(IsFull(H)) return;
i = ++H->size; //CBT顺序下的第一个空位的下标,即完成插入后堆的最后一个元素位置
for(;item>H->data[i/2];i/=2)
H->data[i] = H->data[i/2]; //向下过滤结点,直到该位置的父节点大于item
H->data[i] = item;
}
Delete
取出根结点(最大值)元素,同时删除堆的一个结点
int DeleteMax(MaxHeap H){
int parent, child; //subscript
int maxItem, tmp;
if(IsEmpty(H)) return;
maxItem = H->data[1];
tmp = H->data[H->size--]; //思路是将最后一个元素放到root,然后往下过滤
for(parent = 1;parent*2 <= H->size;parent = child){
child = parent*2;
//取两个child中的大者
if( (child!=H->size) && (H->data[child] < H->data[child+1]) ) child++;
if(tmp >= H->data[child]) break;
else H->data[parent] = H->data[child];
}
H->data[parent] = tmp;
return MaxItem;
}
Build
思路一:通过插入操作,一个一个插入空堆。 \(T = O(N\log N)\)
思路二:将元素按顺序输入,满足CBT结构特性。再调整各节点位置,以满足最大堆特性。
\(T=O(N)\)
void PercDown( MaxHeap H, int p )
{ /* 下滤:将H中以H->Data[p]为根的子堆调整为最大堆 */
int Parent, Child;
ElementType X;
X = H->Data[p]; /* 取出根结点存放的值 */
for( Parent=p; Parent*2<=H->Size; Parent=Child ) {
Child = Parent * 2;
if( (Child!=H->Size) && (H->Data[Child]<H->Data[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= H->Data[Child] ) break; /* 找到了合适位置 */
else /* 下滤X */
H->Data[Parent] = H->Data[Child];
}
H->Data[Parent] = X;
}
void BuildHeap( MaxHeap H )
{ /* 调整H->Data[]中的元素,使满足最大堆的有序性 */
/* 这里假设所有H->Size个元素已经存在H->Data[]中 */
int i;
/* 从最后一个结点的父节点开始,到根结点1 */
for( i = H->Size/2; i>0; i-- )
PercDown( H, i );
}
d-Heap
上面的堆为二叉堆,即2-heap。d代表每个结点最多有d个孩子。
child与parent的关系:
- \(child(i,j) = d*(i-1)+2+j,i为父亲下标,j表示第几个孩子,0<j<d-1\)
- $lastHaveLeaf = (size+1)/d,d-heap最后一个有叶子的结点 $
哈夫曼树(Huffman Tree)
带权路径长度(WPL):\(WPL=\sum_{k=1}^n w_kl_k\);
哈夫曼树(最优二叉树)即WPL最小的二叉树。
构造
思路:每一轮将权值最小的两二叉树合并为一个新的二叉树
typedef struct TreeNode *HuffmanTree;
struct TreeNode{
int weight; //权值
HuffmanTree Left, Right;
}
HuffmanTree Huffman(MinHeap H){
//假设H->size个权值已存入H->data->weight;
int i;
HuffmanTree T;
BuildMinHeap(H); //将H->data按weight调整为最小堆
for(i = 1;i<H->size;i++){ //做H->size-1次合并
T=(TreeNode)malloc(sizeof(struct TreeNode));
T->Left = DeleteMin(H);
T->Rgiht = DeleteMin(H);
T->weight = T->Left->weight + T->Right->weight;
Insert(H,T); //将T插入最小堆
}
T = DeleteMin(H);
return T;
}
特点
- 没有
degree = 1的结点 leaf = n-->total = 2n-1- 左右子树交换不影响性质
- 同一组权值存在不同构的哈夫曼树
- 字符均在叶节点,内部结点为权值和
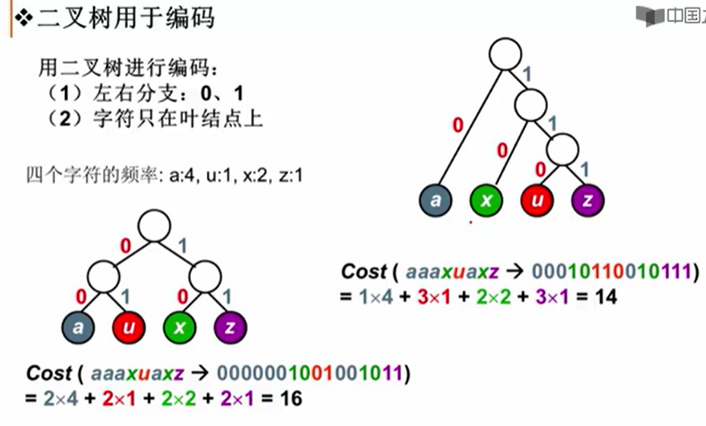
哈夫曼编码
即,在哈夫曼树里,左子树取0,右子树取1
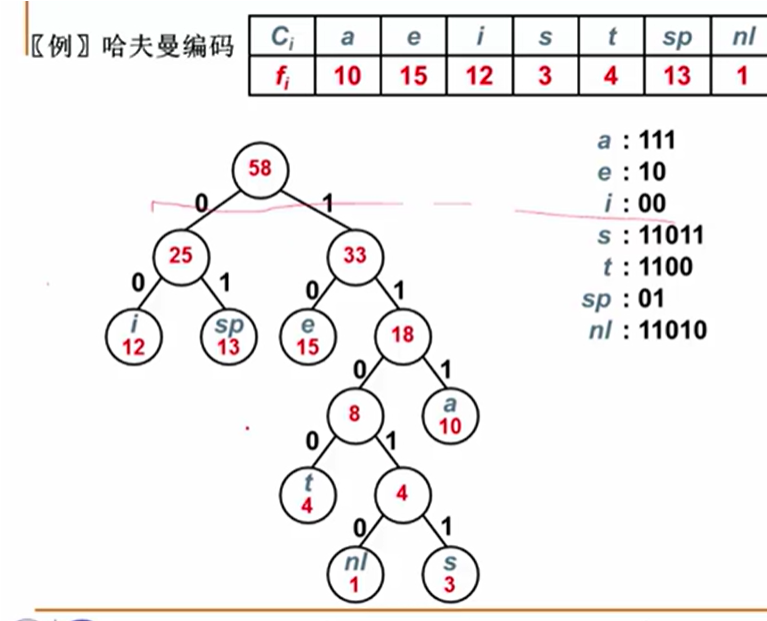
二叉树编码问题
前缀码:任何字符的编码都不是另一字符编码的前缀
- 如果字符均在叶节点,则能避免二义性。
- 若某字符是另一字符的父结点,则有二义性。
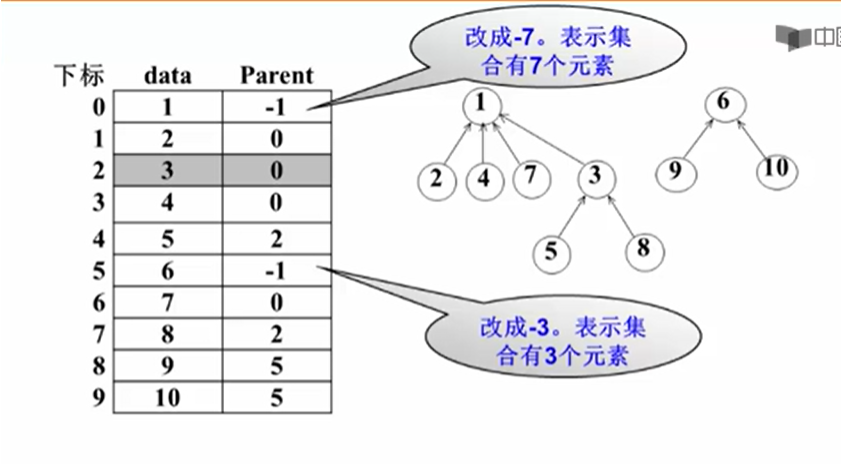
集合(Union)
集合分很多种,这里主要讲并查集。它管理一系列不相交的集合,并支持两种操作:
- 合并(Union):把两个不相交的集合合并为一个集合。
- 查询(Find):查询两个元素是否在同一个集合中。
双亲表示法:每个元素指向一个标志元素,以表示属于该集合。
数组存储形式
集合运算
define
Find
寻找X所在的集合,返回标志元素的下标。
int Find(SetType S[], int X){
int i;
for(i = 0;i<MaxSize && S[i].Data!=X;i++);
if(i>=MaxSize) return -1;
for(;S[i].parent >= 0;i=S[i].parent);
return i;
}
Union
void Union(SetType S[],int X1,int X2){
int root1,root2;
root1 = Find(S,X1);
root2 = Find(S,X2);
if(root1!=root2) S[root2],parent = root1;
}
为了改善性能,合并时选择将小集合并入大集合;
此时最大深度为 \(\log_2N+1\)
#define MAXN 1000 /* 集合最大元素个数 */
typedef int ElementType; /* 默认元素可以用非负整数表示 */
typedef int SetName; /* 默认用根结点的下标作为集合名称 */
typedef ElementType SetType[MAXN]; /* 假设集合元素下标从0开始 */
void Union( SetType S, SetName Root1, SetName Root2 ) {
/* 这里默认Root1和Root2是不同集合的根结点 */
/* 保证小集合并入大集合 */
if ( S[Root2] < S[Root1] ){ /* 如果集合2比较大 */
S[Root2] += S[Root1]; /* 集合1并入集合2 */
S[Root1] = Root2;
}else{ /* 如果集合1比较大 */
S[Root1] += S[Root2]; /* 集合2并入集合1 */
S[Root2] = Root1;
}
}
SetName Find( SetType S, ElementType X ) {
/* 默认集合元素全部初始化为-1 */
if ( S[X] < 0 ) /* 找到集合的根 */
return X;
else
return S[X] = Find( S, S[X] ); /* 路径压缩 */
}
路径压缩是一种优化技术,用于在并查集数据结构中的Find操作中减少查找路径的长度。
在传统的Find操作中,为了找到一个元素的根节点,我们需要遍历从该元素到根节点的路径,并返回根节点。
路径压缩通过修改指向根节点的指针,将路径上的所有节点直接连接到根节点上,从而将整个路径压缩成长度为1的链。
路径压缩的实现通常使用递归或迭代方式进行。
当执行Find操作时,如果当前节点不是根节点,那么就将其父节点更新为根节点,并递归地进行路径压缩。
路径压缩的目标是使得后续的Find操作更加高效。通过路径压缩,查询一个元素的根节点的时间复杂度可以达到接近O(1)的水平,有效提升了并查集的性能。
Relation
自反关系(reflexive)
设 R是 A上的一个二元关系,若对于 A中的每一个元素 a, (a,a)都属于 R,则称 R为自反关系。
非自反关系(irreflexive)
设R是A上的关系。若对所有a∈A,均有(a,a)∈ R,则称R是A上的一个自反关系
对称关系(symmetric)
集合A上的二元关系R,对任何a,b∈A,当aRb时有bRa
非对称关系(asymmetric)
集合A上的二元关系R,对任何a,b∈A,当aRb时有bR a
反对称关系(antisymmetric)
consistent相容关系
指集合A上具有自反性与对称性的二元关系。定集合A上的关系R,若R是自反的、对称的,则称R是A上的相容关系。相容关系R只要求满足自反性与对称性,因此,等价关系必定是相容关系但反之不真
transitive传递关系
指由甲、乙和乙、丙都有,可推知甲、丙也有的那种关系。集合A上的二元关系R,对任何a,b,c∈A,当aRb,bRc时,有aRc,用符号表示:R是A上的传递关系⇔∀a∀b∀c(a∈A∧b∈A∧c∈A∧aRb∧bRc→aRc)。