CP-Homework2

:material-circle-edit-outline: 约 566 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

[!ABSTRACT]

Modern Compiler Implementation in C.pdf P85

3220104929 250306

3.6

（a）

	nullable	FIRST	FOLLOW
S	no	u
B	no	w	z, v, x, y
D	yes	x, y, \(\epsilon\)	z
E	yes	y, \(\epsilon\)	z, x
F	yes	x, \(\epsilon\)	z

(b)

	u	v	w	x	y	z
S	uBDz
B			Bv, w
D				EF	EF
E				\(\epsilon\)	y	\(\epsilon\)
F				x		\(\epsilon\)

(c)

T[B,w] 项有两个 production，所以这个文法不是 LL(1) 的

(d)

为了使其转化为最小的 LL(1)文法，需要消除左递归

将 \(B\rightarrow Bv|w\) 转化为 \(B\rightarrow wT,T\rightarrow vT|\epsilon\)，其它不变即可

3.9

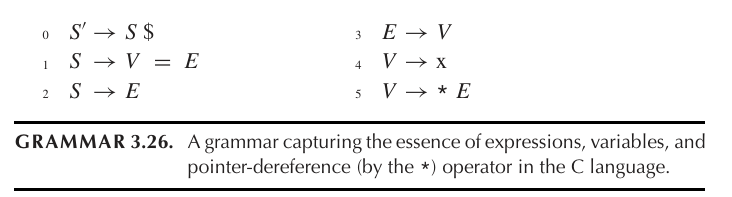
我们可以得到 LR(0) Item 的 NFA：

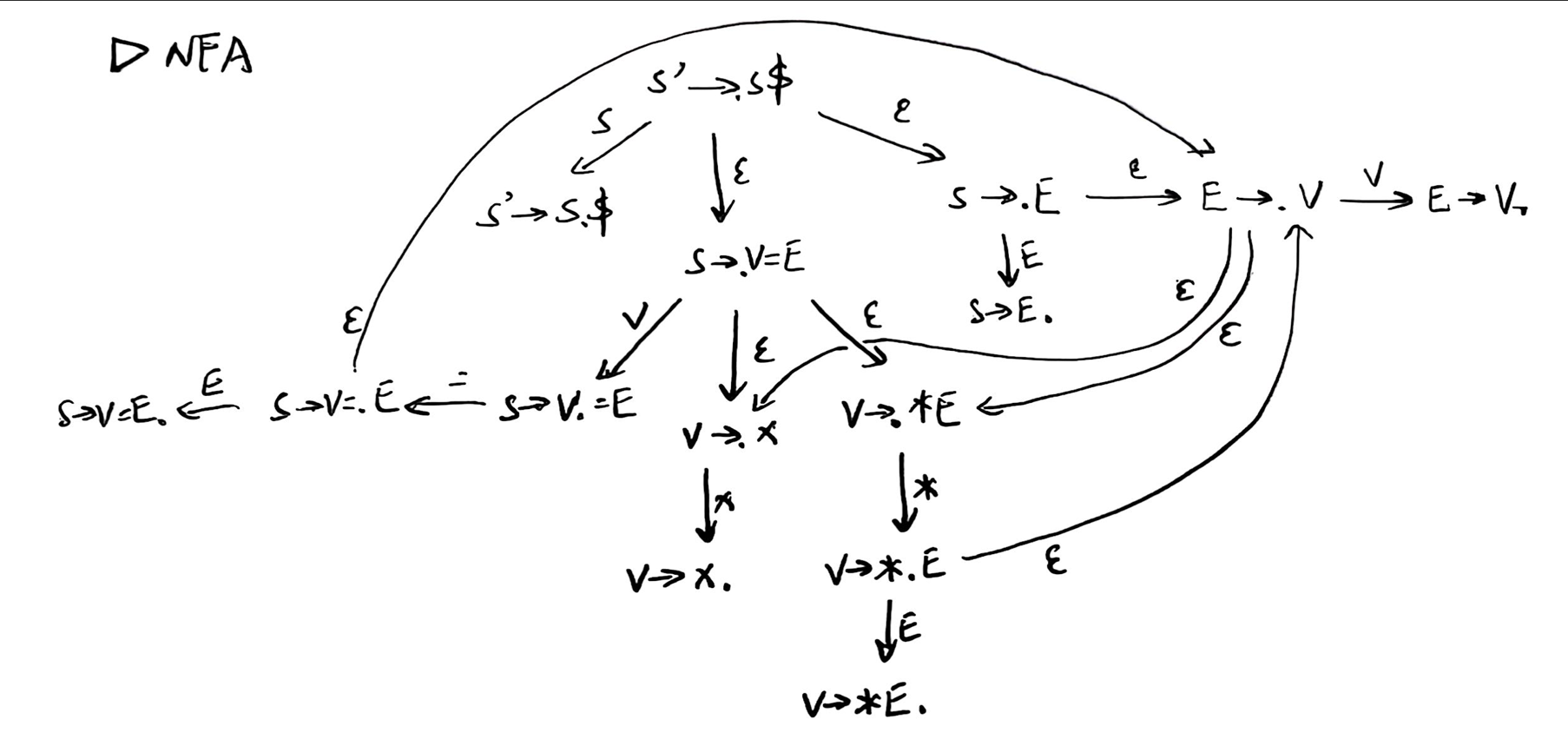
将其转化为 DFA：

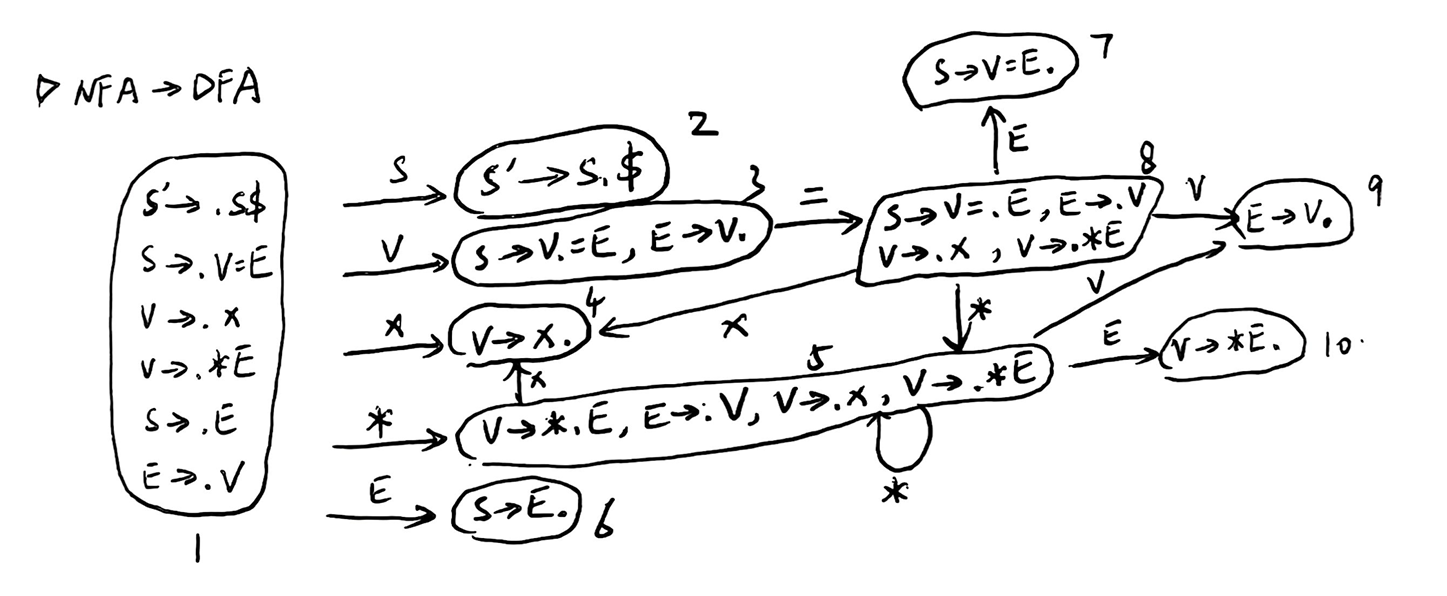
再获取各个非终结符的 follow 集合：

• \(Follow(S) = \{\$\}\)
• \(Follow(V) = \{=,\$\}\)
• \(Follow(E) = \{=,\$\}\)

据此可以构造出一个 SLR(1) Parsing Table：

	S	$	E	V	x	*	=
1	g2		g6	g3	s4	s5
2		accept
3		r3					s8, r3
4		r4					r4
5			g10	g9	s4	s5
6		r6
7		r7
8			g7	g9	s4	s5
9		r9					r9
10		r10					r10

出现冲突的项是 T[3,=]

3.13

我们可以得到 LR(1) Item 的 NFA：

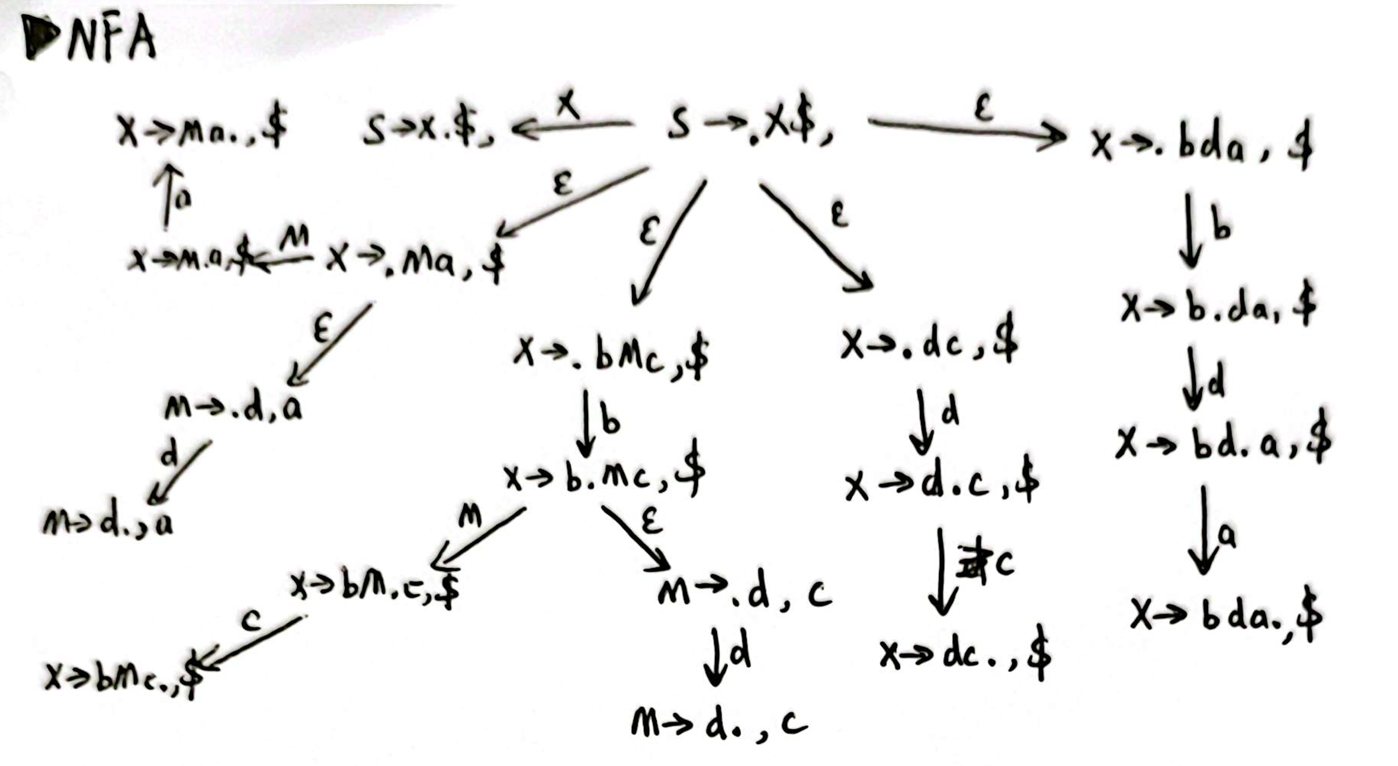
将其转化为 DFA：

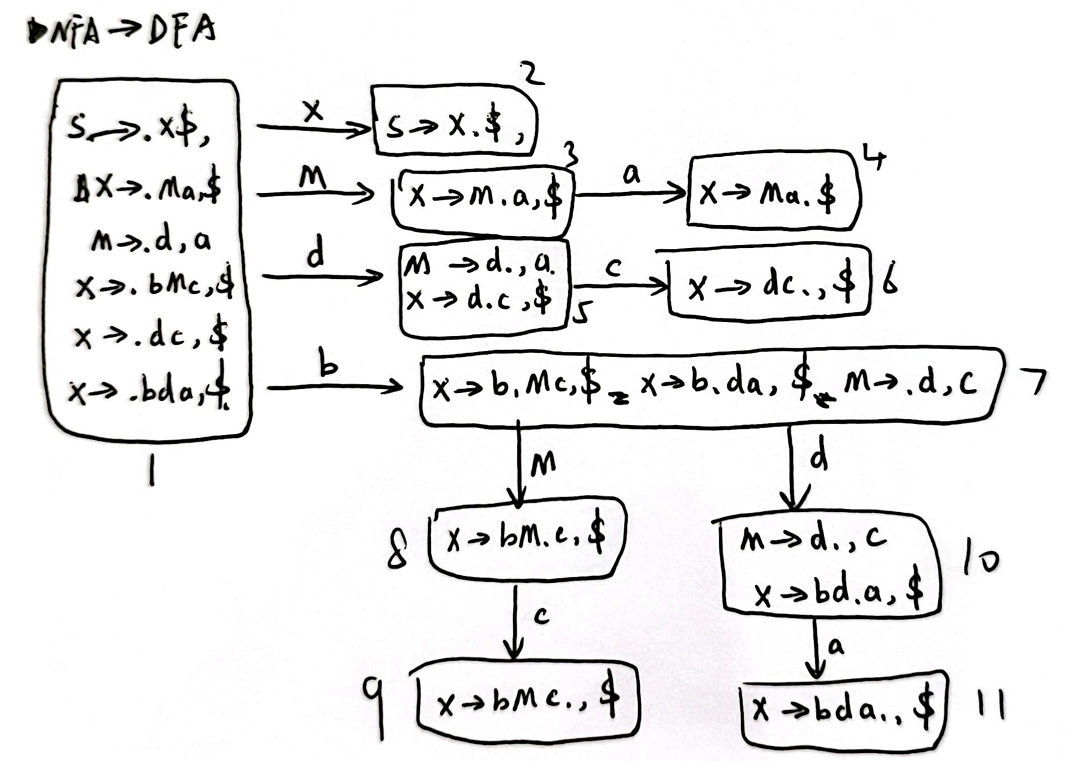
据此可以构造出一个 LALR(1) Parsing Table：

	X	M	$	a	b	c	d
1	g2	g3			s7		s5
2			accept
3				s4
4			r1
5				r5		s6
6			r3
7		g8					s10
8						s9
9			r2
10				s11		r5
11			r4

可以看到不存在冲突项，所以该语法是 LALR(1)文法

我们可以得到 LR(0) Item 的 NFA：

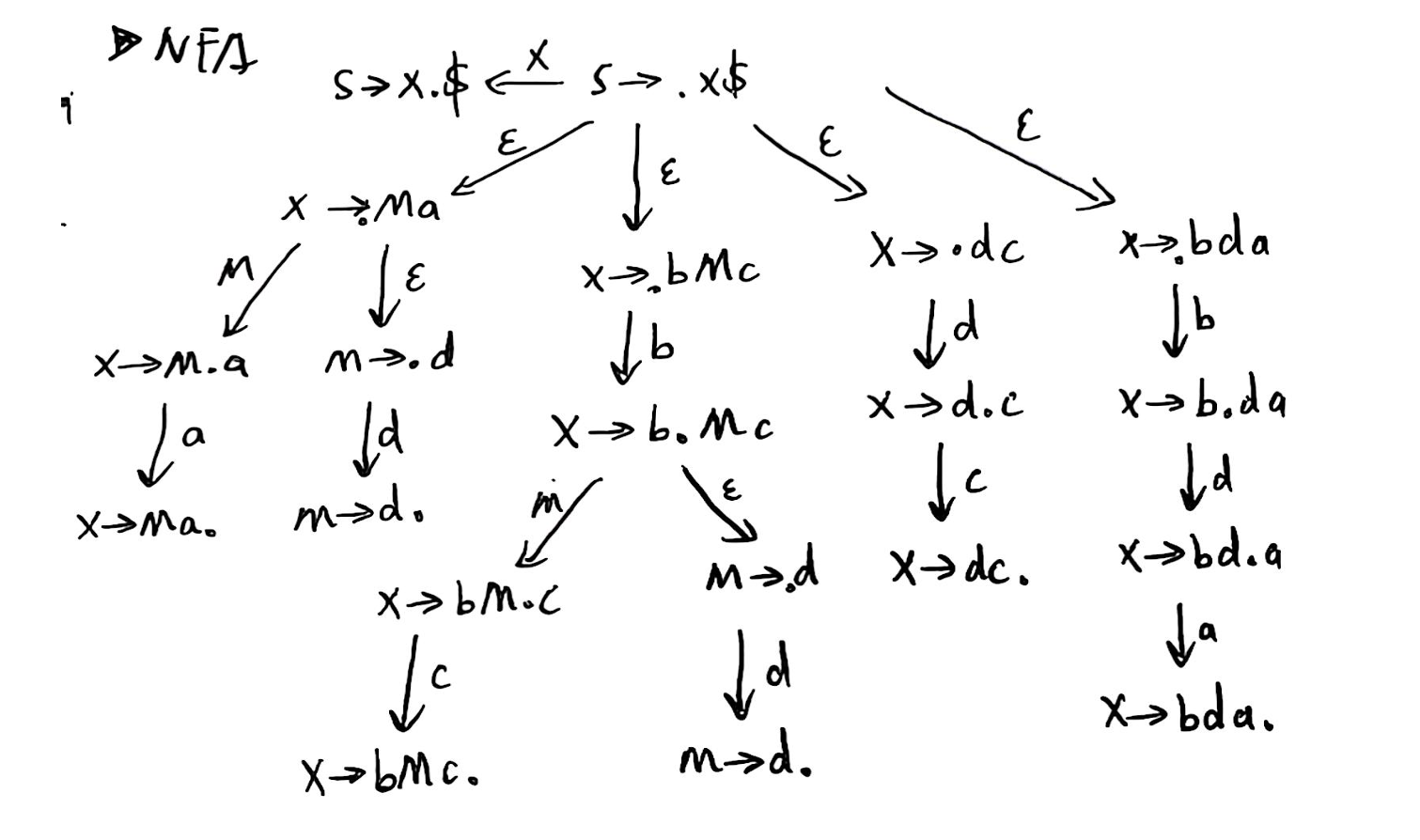
将其转化为 DFA：

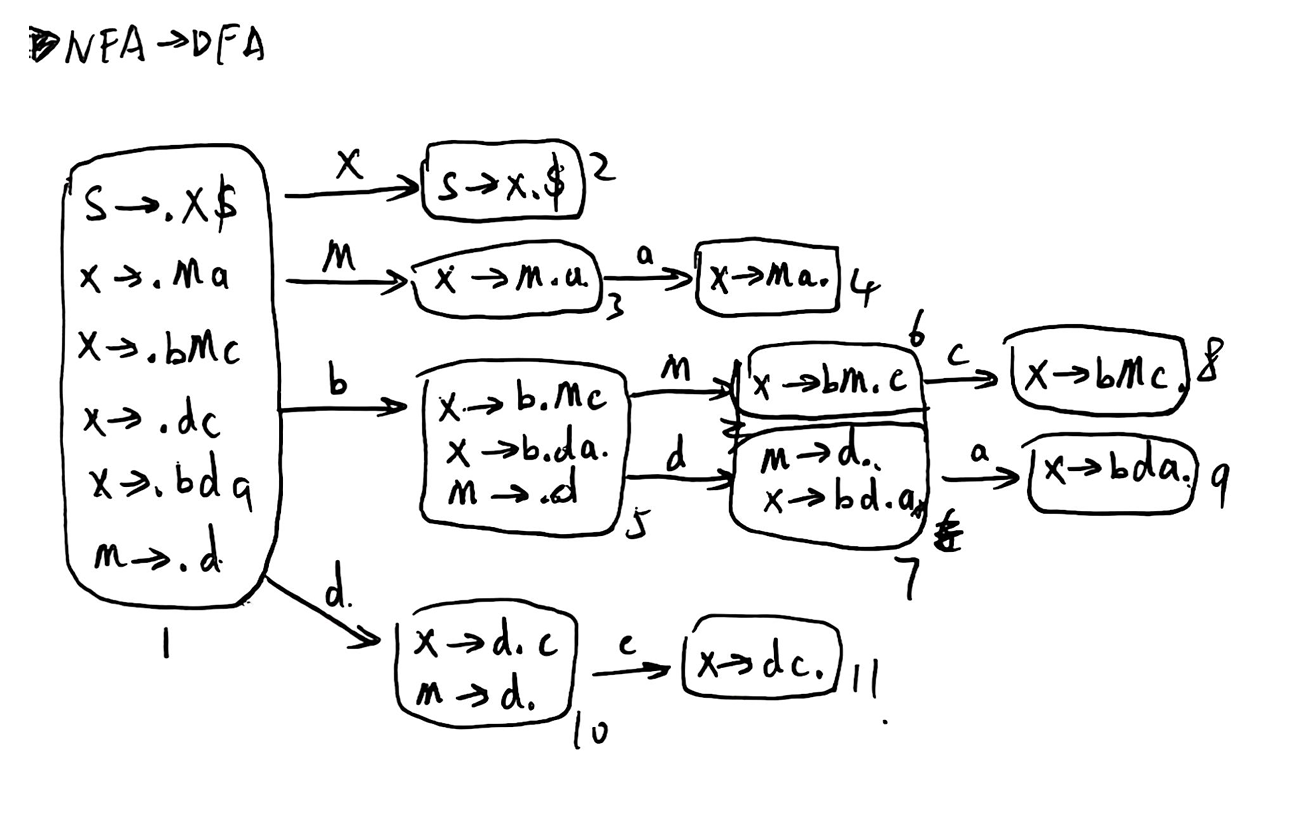
获取非终结符的 follow 集合：

• \(Follow(X) = \{\$\}\)
• \(Follow(M) = \{a,c\}\)

据此可以构造出一个 SLR(1) Parsing Table：

	X	M	$	a	b	c	d
1	g2	g3			s5		s10
2			accept
3				s4
4			r1
5		g6					s7
6						s8
7				r5, s9		r5
8			r2
9			r4
10				r5		s11, r5
11			r3

可以看到存在冲突项 T[7,a], T[10,c]，所以该文法不是 SLR(1) 文法

3.14

	nullable	FIRST	FOLLOW
S	no	(, ], )
X	no	), ]
E	yes	\(\epsilon\)	], )
F	yes	\(\epsilon\)	], )
A	yes	\(\epsilon\)	], )

据此可以构造出一个 LL(1) Parsing Table：

	]	(	)
S	E]	(X	F)
X	F]		E)
E	A		A
F	A		A
A	\(\epsilon\)		\(\epsilon\)

可以看到不存在冲突项，所以该语法是 LL(1)文法

对于该文法，我们增加一个起始符号 \(S^\prime\) 以及对应的产生式 \(S^\prime \rightarrow S\$\) ，我们可以得到 LR(1) Item 的 NFA：

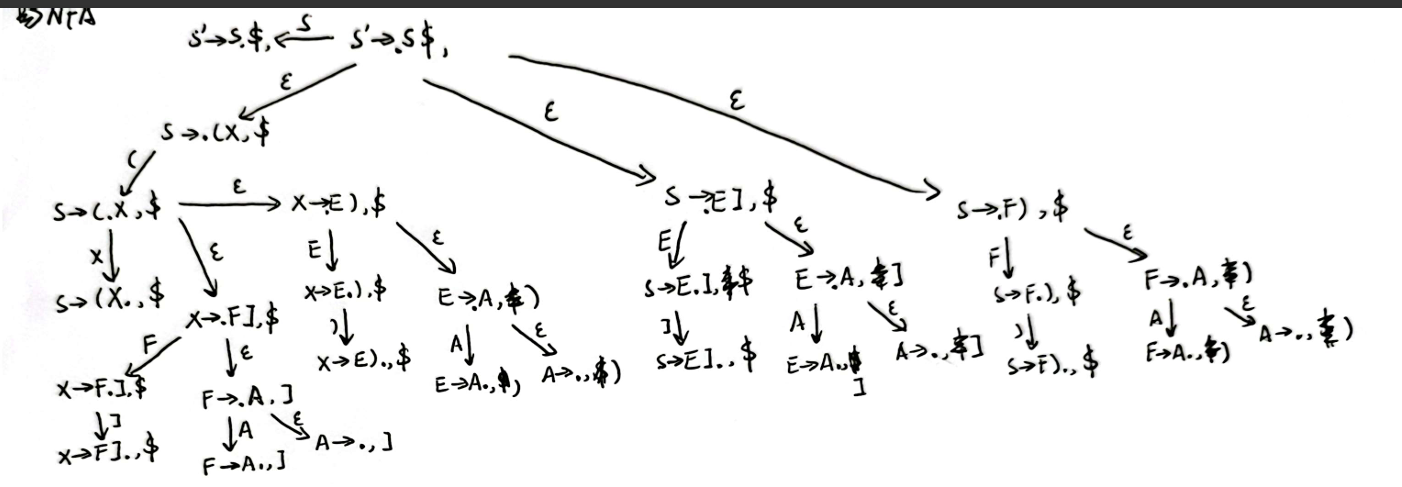
将其转化为 DFA：

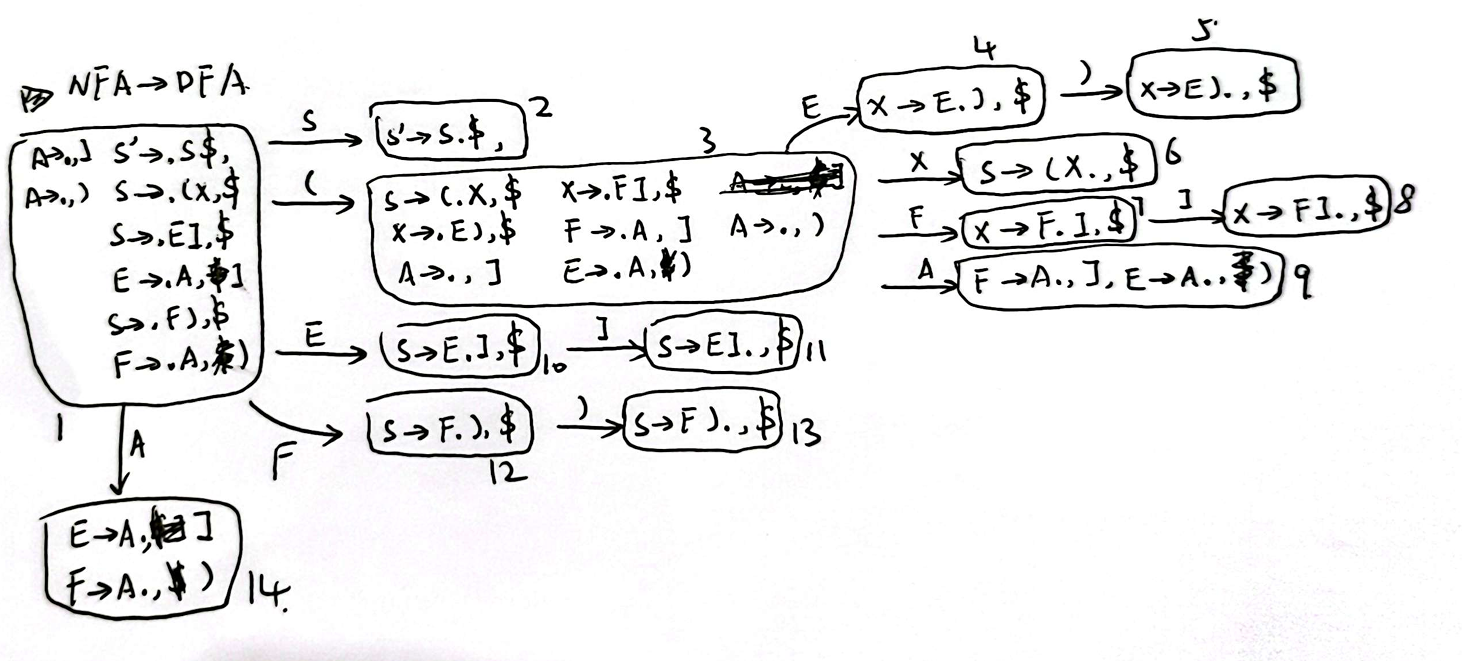
如上图所示，state 9 和 state 14 具有相同的核心，但合并后会出现 reduce-reduce conflict，所以该文法不是 LALR(1)文法