Instruction Selection
开始将规范树转化为汇编代码了

Instruction Selection:apping IR into abstract assembly code
Register Allocation:Deciding which values will reside in registers,Replace abstract registers with real register
Instruction Selection: Why and What
The intermediate representation (Tree) language expresses only one operation in each tree node.
Areal machine instruction can often perform several of primitive operations.
The instruction selection phase: Finding the appropriate machine instructions to implement a given intermediate representation tree
Tree Patterns
Each machine instruction can be expressed a fragment of an IR tree, called a tree pattern.
Instruction selection: tiling the tree with a minimal set of tree patterns.
Tiling: cover the tree with nonoverlapping tree patterns
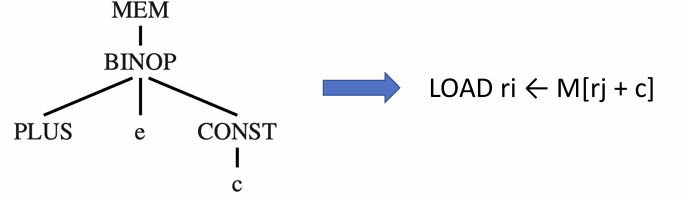
The tiles are the set of tree patterns corresponding to legal machine instructions
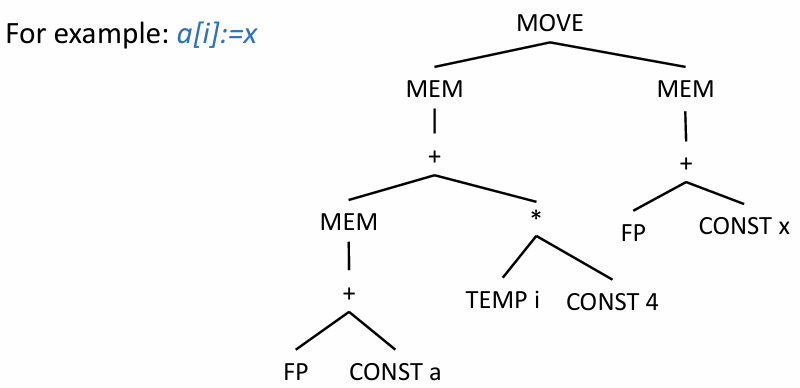
To illustrate instruction selection, we use the Jouette architecture invented in the textbook
The Jouette architecture
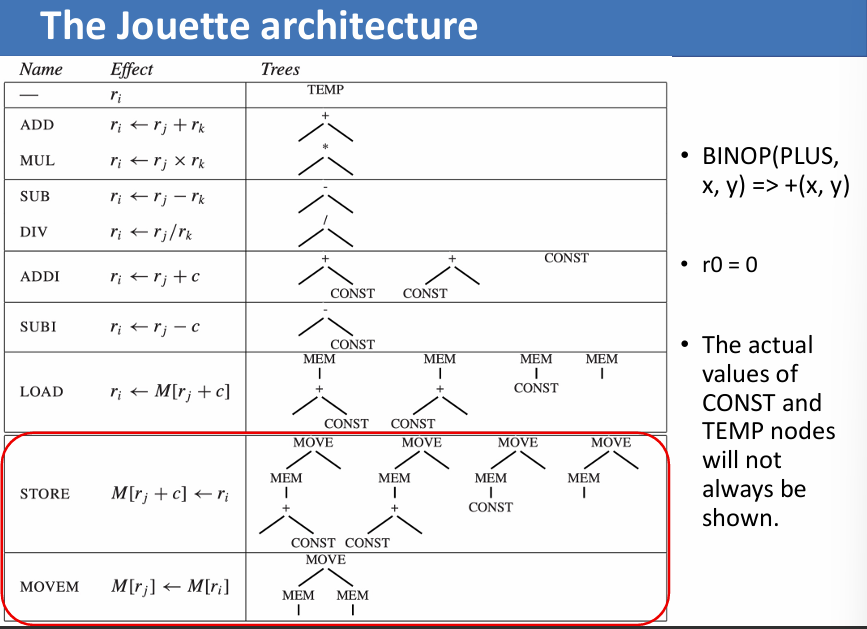
Specification about Jouette Architecture
Register r0 always contains zero
Some instructions correspond to more than one tree pattern
Tree Patterns- Example
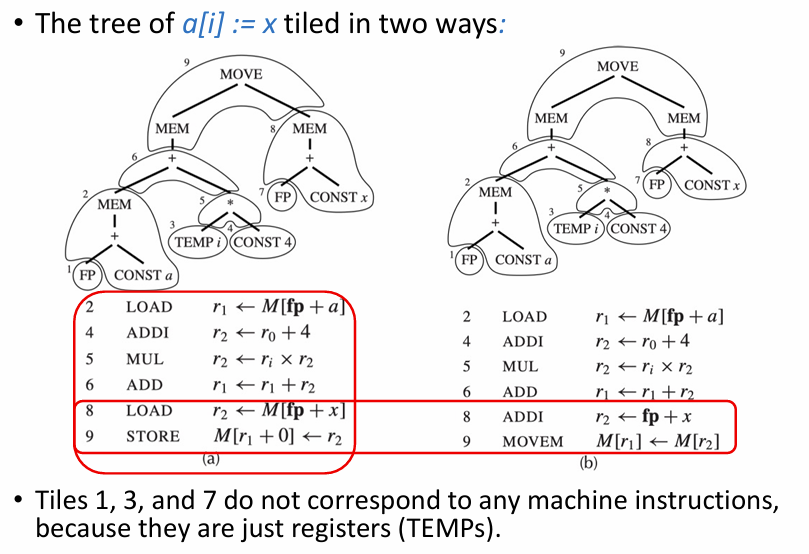
It is always possible to tile the tree with tiny tiles, each covering only one node
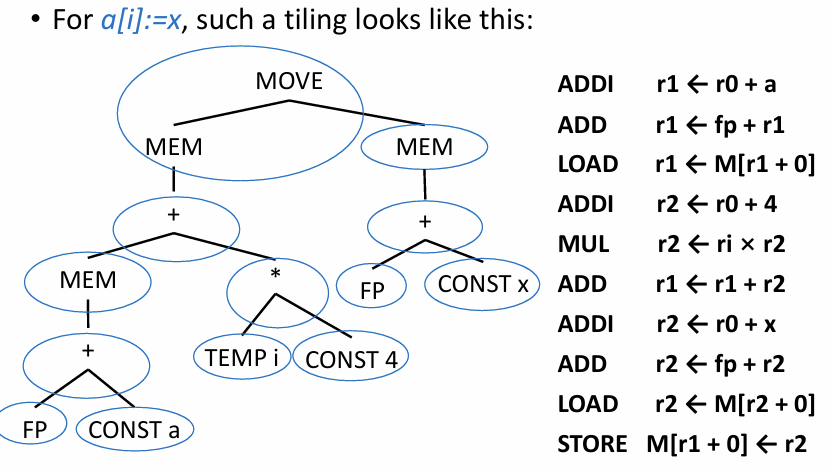
Optimal and Optimum Tilings
- Best tiling: an instruction sequence of least cost
- the shortest sequence of instructions
- Orthe least-cost sequence has the lowest total time if the instructions take different amount of time to execute.
- Optimum tiling: the one whose tiles sum to the lowest possible value
- 全局最优,cost 最小的覆盖
- Optimal tiling: the one where no two adjacent tiles can be combined into a single tile of lower cost
- 局部最优,如果选择任意两个瓦片进行合并,代价没有变得更低,那么当前的就是最佳(Optimal)覆盖
- Every optimum tiling is also optimal, but not vice versa
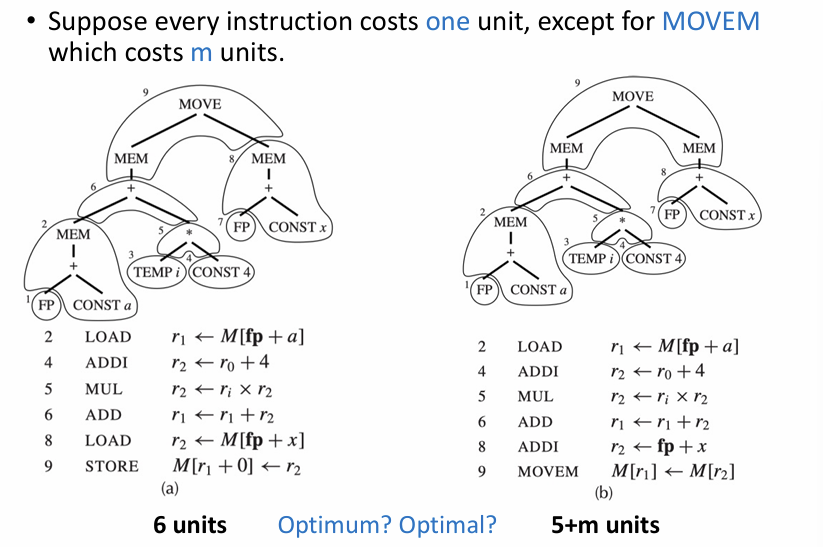
Algorithms for Instruction Selection
Maximal Munch
always finds an optimal tiling, but not necessarily an optimum
- Assume larger tiles = better
- Main idea: Greedy algorithm
- 自顶向下遍历 IR tree,用尽可能大的瓦片进行覆盖当前的结点,再递归检查剩下的
- 能保证任意两个瓦片都不能合并
Largest tile: the one with the most nodes
- 具体流程
- Starting at the root of the tree, find the largest tile that fits.
- Cover the root node– and perhaps several other nodes near the root– with this tile, leaving several subtrees.
- Repeat the same algorithm for each subtree.
The instructions are generated in reverse order
If twotiles of equal size match at the root, then the choice between them is arbitrary

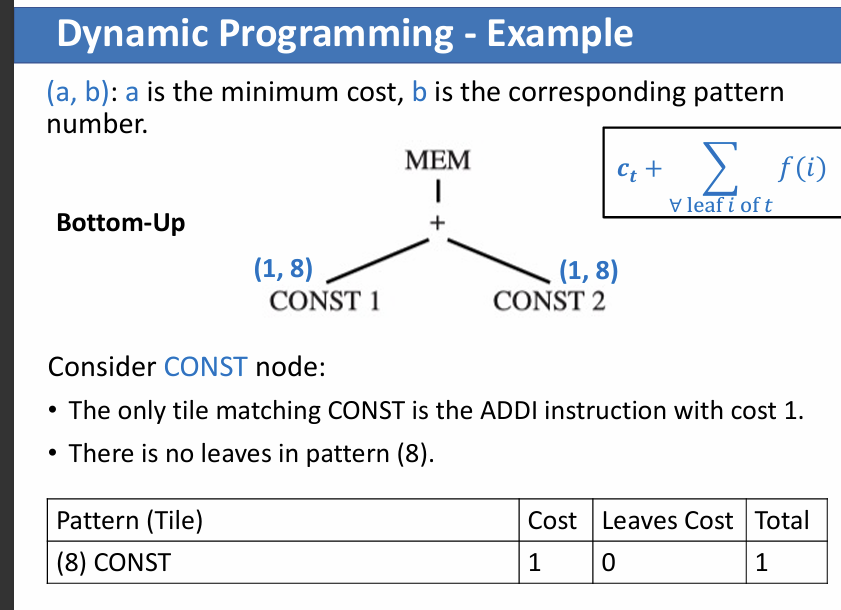
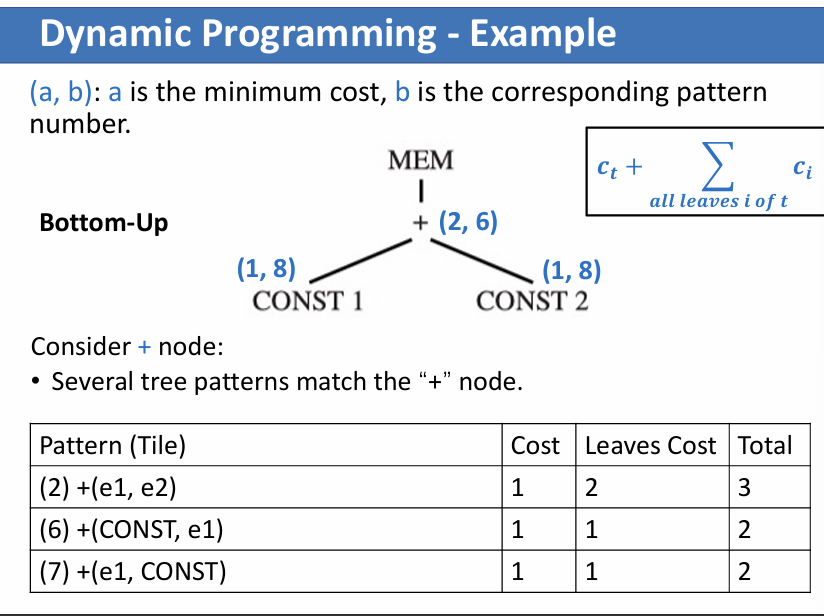
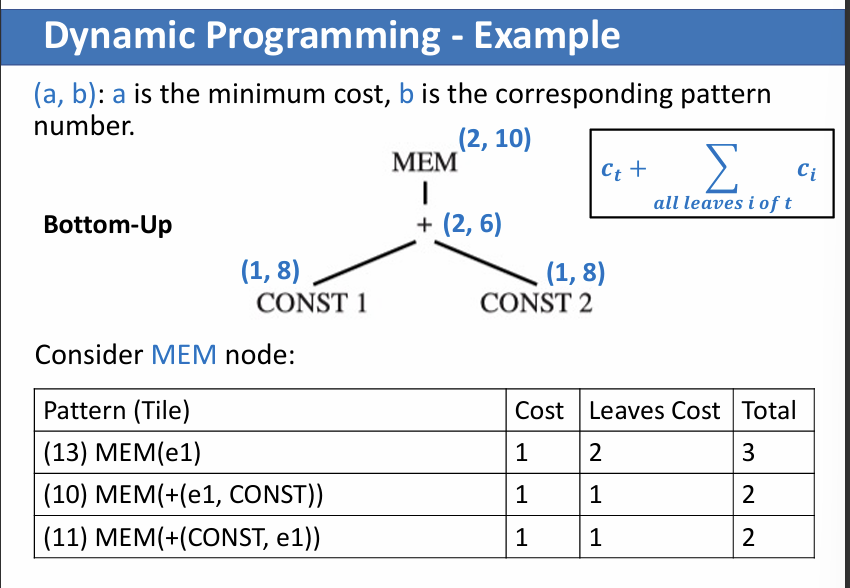
Dynamic Programming
can find the optimum based on the optimum solution of each subproblem
- It works bottom-up
- Assign a cost to every node in the tree



Tree Grammar
tree patterns 可能会非常多,非常复炸,人工实现 tiling 算法很麻烦
我们就希望用 Tree Grammar 描述 tree patterns,使用一个通用的动态规划算法来解析 Tree Grammar 生成 inst selector
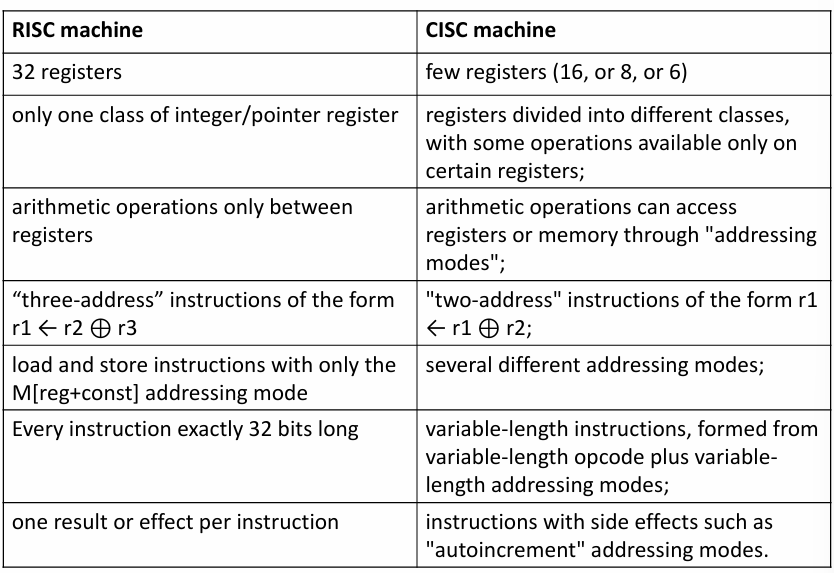
CISC Machines
我们之前都是 RISC 机器,如果是 CISC 机器有更多问题要解决