Skip to content

Lexical Analysis

:material-circle-edit-outline: 约 600 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

Regular Expressions

  • [abcd] 表示 (a|b|c|d)
  • [b-gM-Qkr] 表示 [bcdefgMNOPQkr]
  • M? 表示 (M|ϵ)
  • M+ 表示 (M·M*)
  • . 表示除换行符外的所有单个字符
  • "a.+*" ，引号中的字符串匹配其自身

NFA 转 DFA

记 \(M^\prime=(K^\prime,\Sigma ,\delta,s^\prime,F^\prime)\) 为 DFA，\(M=(K,\Sigma ,\Delta,s,F)\) 为 NFA，他们是等价的

则：

  • \(K^\prime=2^K\)
  • \(s^\prime=E(s)\)
  • \(F^\prime=\{Q|Q\subseteq K,Q\cap F\neq\empty\}\)
  • 转移方程：

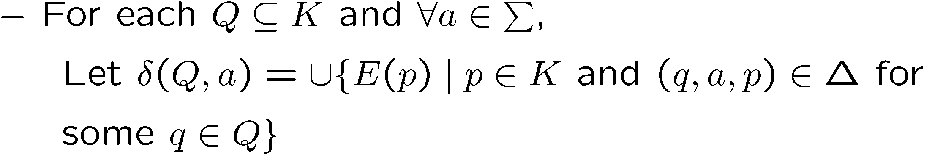
image-20241014104223738

也就是说，我们取 NFA 状态的集合作为 DFA 的一个状态

对于 NFA 所有可能的状态集合，其转移方程为，集合内所有状态的转移关系的结果的 E()

从 \(s^\prime=E(s)\) 往后推即可

注意转换后的 DFA 状态都是 集合，是 NFA 状态的集合

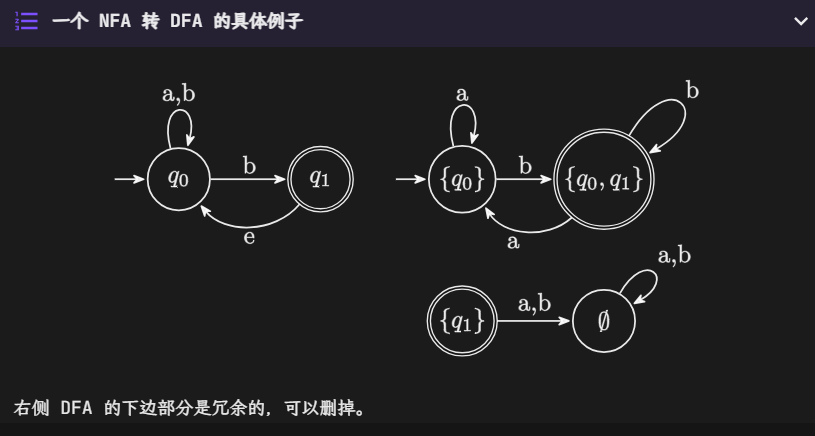
image-20241231105850436

DFA 最小化

算法描述：

  1. 将目前的终止状态放入一个集合，将其它状态放入另一个集合
  2. 遍历字母表，如果两个状态输入相同的字符转化到不同的状态，则拆分到不同集合，如果相同则保留在同一个集合
  3. 遍历结束后，处于同一集合的状态属于等价状态，合并为新状态
  4. 回到步骤 1，直到步骤 2 没有拆分出任何新集合

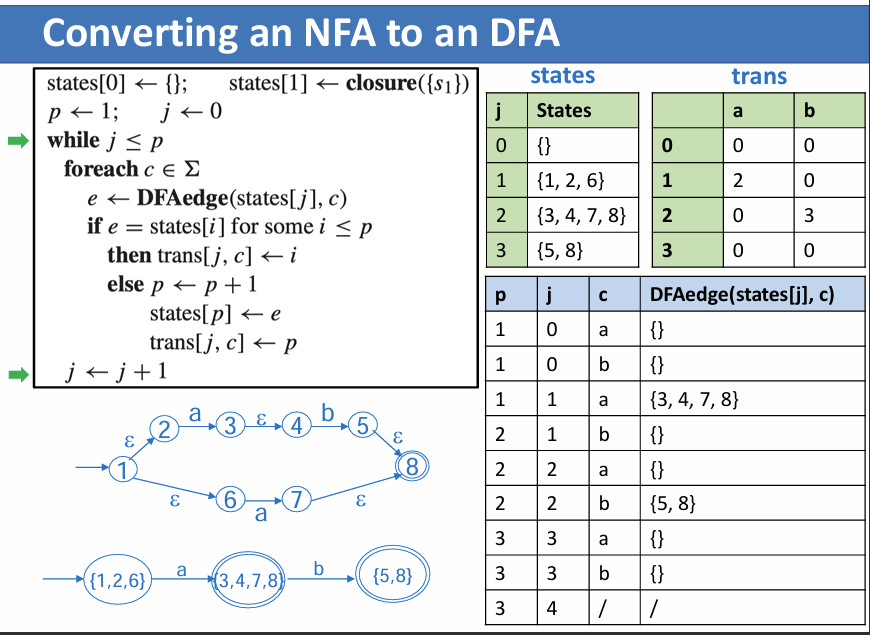
image-20250326163415309

其实就是先取所有通过 \(\epsilon\) 相连的状态组成新的集合作为 DFA 的状态，然后按字母表有序地检查：当每一个字符输入后，状态集合里各个状态会转化到哪些状态，将其组成集合作为新的状态。如此往复，直到找不出新的状态为止

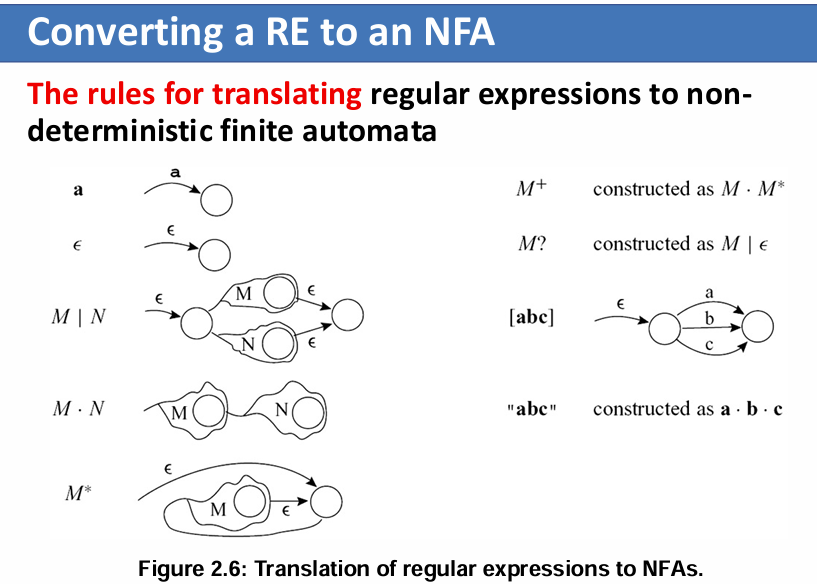
image-20250326195640148

助教说最好按左边的样子来画

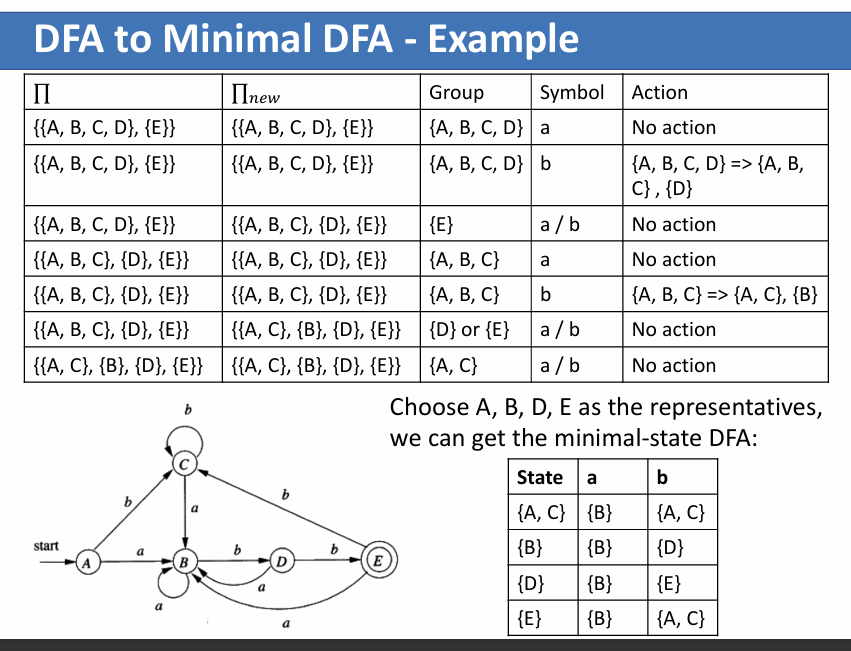
image-20250326220134892

简单来说，就是初始化为 \({S-F,F}\) 两个状态集合，然后每轮循环里对所有集合进行检查：遍历字母表，检查集合里各个状态是否转换到了相同状态，如果不是，则将转换到相同状态的状态取出来组成新集合。如此循环，直到一轮检查后没有新的集合出现。

Lex

Lex 和其他类似的词法分析器中规定了两条规则以消除二义性：

  • Longest Match : 输入的字符串中的最长的能与任一正则表达式匹配的子串为匹配到的 token
  • Rule Priority : 对匹配到的 longest substring，选择第一个与之匹配的正则表达式