Skip to content

Register Allocation

:material-circle-edit-outline: 约 738 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

Register allocation (Graph coloring) is an NP-complete problem

Coloring By Simplification

Build & Simplify

首先画图，每个结点代表一个变量，一条边代表他们有冲突（不能被分配同一个 reg）

然后对图进行化简，记我们有 k 个 reg，如果一个结点的邻居数量少于 k，就删掉这个结点

即，一个结点的邻居数量少于 K，那么我染色完它的邻居，一定能留一个寄存器给它

然后用 stack 按序储存删掉的结点，如此不断重复，直到没结点了，或剩下的都是 significant degree 的结点（邻居数 \(\ge\) k）

Spill

只剩下 significant degree 的结点时，我们选择一些结点储存到 mem 而非 reg 里，这些节点与其它结点不再冲突，然后我们会将其删除并 push 进 stack

spill 后继续 Simplify，如此循环，直到生成空图

下图中 spill 了 b

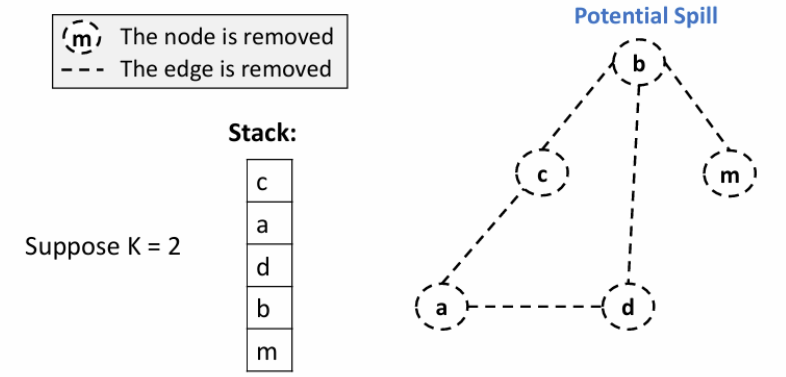
image-20250615162817027

Select

从 stack pop 结点，一个一个染色，重建冲突图

乐观染色：这里的 b 虽然被设置为了 Potential Spill，此时已有两个邻居染色，但这里要染它时是由空闲颜色的，所以可以染色，其不是 actual spill

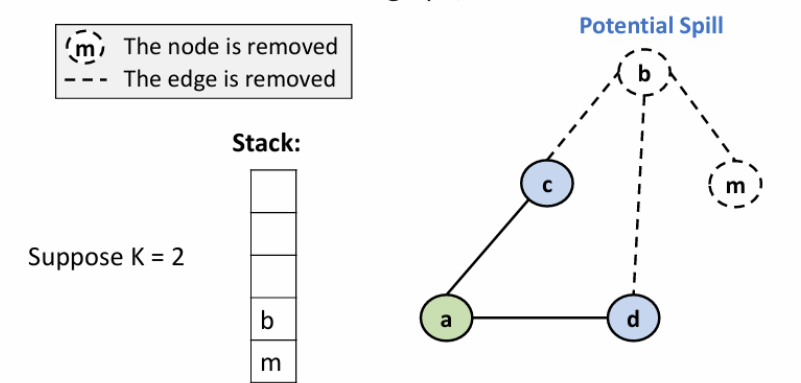
image-20250615163023231

每次发现 actual spill 就得对原程序增加相应的内存访问指令：

  1. fetch them from memory just before each use
  2. and store them back after each def.

然后由于程序被重构，我们又可以构建新的冲突图，在重复上面的步骤

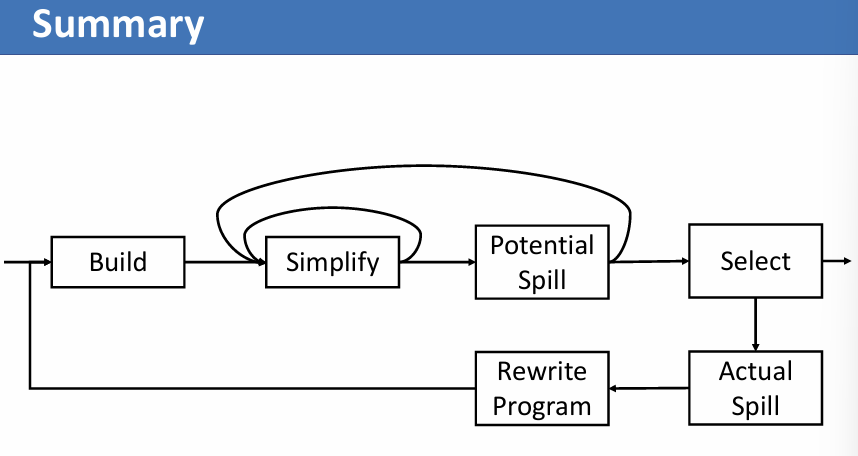
image-20250513155236263

Coalescing

如果两个结点是虚线（合并边）连接的，即这其中一个变量复制于另一个变量，且二者没有冲突边，那么就可以将他俩合并

但是新节点的邻居可能变多，所以我们采取保守合并，保证合并后的图不会变成非 k-colorable graph

有两种具体的实现方式

  1. Briggs
    • 新节点应当有少于 K 个邻居是 significant degree 的
    • 确保 simplify 后能剩下少于 K 个邻居，于是新节点也可以被 simplify 掉
  2. George
    • 对于合并前的 A 和 B，需满足其中一个条件：
      • A 所有邻居都与 B 有冲突
      • A 所有邻居都是 insignificant degree
    • 符合第一个条件的边不会被重复增加至新节点
    • 符合第二个条件的边能被优化
    • 于是新节点的边被压制在 B 合并前的数量

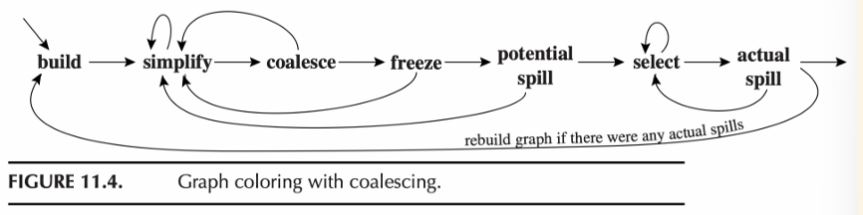
image-20250615164622195

注意：

  1. build 时需要注意 MOVE 并画出合并边
  2. simplify 先只处理非 MOVE 相关结点
  3. Coalescing 后再 simplify，二者循环直至去除所有合并边
  4. 如果没法去除所有合并边，进入 freeze 阶段，找一个 low degree 的 MOVE 相关结点，我们 freeze 这个 MOVE 操作，将虚线变为实线，放弃合并

Precolored Nodes

预着色结点与其它所有结点冲突，且无法被删除，无法被 spill

我们的目标就不是生成空图，而是生成只剩下 Precolored Nodes 的图

Chapter11.pdf 75有例子