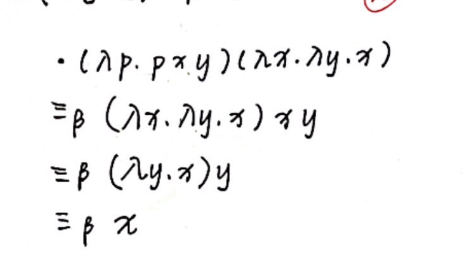Skip to content

\(\lambda\) 演算

:material-circle-edit-outline: 约 1514 个字 :material-clock-time-two-outline: 预计阅读时间 5 分钟

\(\lambda\) 演算里面全是表达式，没有语句

表达式和语句

编程语言由表达式或语句组成，表达式是有结果（value）的式子，语句本身是不确定的，例如逻辑判断语句

定义

一个复杂的PL可以被形式化为两部分，一个是核心演算 \(\lambda\) 演算，一个是可被翻译为 \(\lambda\) 演算的导出形式

\(\lambda\) 演算将所有的计算都归约到函数定义和函数应用这样的基本操作

\(\lambda\) 演算是一个系统，在这个系统里函数可以被当作另一个函数的参数

\(\lambda\) 演算是由特定形式语法所组成的一种语言，其基本项叫 \(\lambda\) 项（term），就像代数里的基本项是数字

\(\lambda\) 演算定义了三类形式不同的基本表达式：

  • 变量（名字）： \(x\) 这个变量本身是一个有效的 \(\lambda\) 项
  • 抽象（定义）：\(\lambda x.t\) 是个 \(\lambda\) 项，前提是 \(x\) 是变量
    • 这个表达式本身描述了一个函数，\(x\) 是形参， \(t\) 是函数表达式
    • 前面的 \(\lambda\) 用于声明这是一个函数
  • 应用（调用）：如果 \(t\) 和 \(s\) 是 \(\lambda\) 项，那么 \(ts\) 也是一个 \(\lambda\) 项
    • \(ts\) 这个项表示 \(t\) 函数输入 \(s\) 参数、

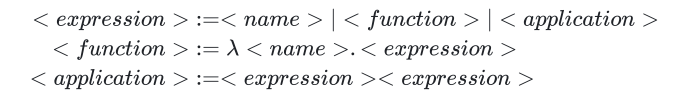
image-20240911145602258

一个 \(\lambda\) 项是有效的，当且仅当 其可由这三种形式组合得到

image-20240911150459139

消歧约定

定义了两个规则，用于避免一个表达式能读出不同含义的情况

image-20240911150624311

  • 在一个括号内（最外层我们假设括号时隐藏的），最左边的 . 囊括其右边所有东西
  • 嵌套应用时应是每轮将最右边的整体单独作为参数往前面一个整体传

自由变量和绑定变量

绑定变量BV 自由变量FV
类比函数形参，\(\lambda\) 旁白那个变量 类比全局变量，BV的补集
可以自由改名，就和形参一样 不能自由改，就像全局变量
只在自己的表达式内部起作用 与其它表达式可能有交互

image-20240911151612523

仔细看懂上面第一个式子

自由变量判定

注意下面 \(FV, BV\) 的值域是变量的名字

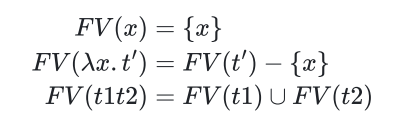
image-20240911211438819

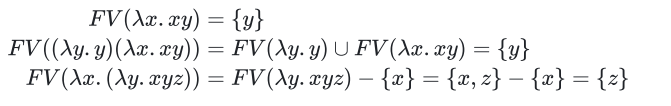
image-20240911152329703

绑定变量判定

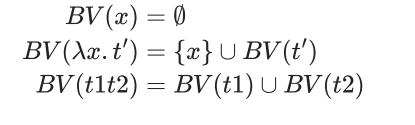
image-20240911211454135

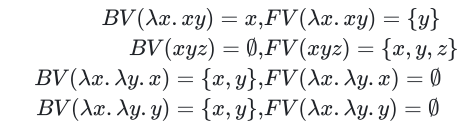
image-20240911152334315

封闭

image-20240911152836213

我们可以推论出，闭项相对于任意项都是封闭的

\(\lambda\) 形式系统

\(\lambda\) 记法是 \(\lambda\) 演算的一部分，这种演算用于对 \(\lambda\) 表达式进行推理，包括公理语义、操作语义和指称语义三种

  • 公理语义是推导表达式之间等式的形式系统
  • 操作语义是基于称为规约（reduce）的等式推理的一种有向形式。用CS的术语来说，规约也可以看作是一种形式的符号计值
  • 指称语义和其他逻辑系统的模型论在精神上是类似的，比如等式逻辑或一阶逻辑

等式语义

Equation Semantics

等式语义包括两种

  • 定义等价：两个函数一模一样，参数名字也一样
  • 语义等价：两个函数形式变一下，运行效果是相同的

代换

我们先讲下一个叫代换的记号

\([N/x]M\) 表示将 \(M\) 里的 \(x\) 替换成 \(N\)，这个操作有个前提，\(BV(M)\cap FV(N) = \emptyset\)

语义等价

语义等价有三种

  • \(\alpha\) 等价就是将函数里的变量名换个名字
  • \(\beta\) 等价就是将函数里的变量名换成要带入的变量名，再去掉 \(\lambda\) 符号（就是带入变量）
    • 而且对象函数得是闭项，毕竟不能将同名的全局变量替换为要带入的形参
  • $\eta $ 等价就是先 \(\beta\) 等价再 $\alpha $ 等价

image-20240911213828653

image-20240911213834048

\(\beta\) 等价又叫 $\beta $ 规约，形式上更像是在化简

image-20240911213841447

下面这张不知道正确答案，去问一下

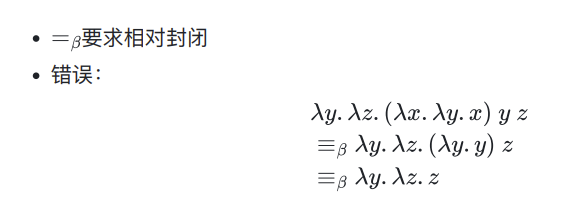
image-20240912094713051

性质

image-20240911154825408

操作语义

image-20240912095041219

替换

正如我们之前用 \(t\) 和 $s $ 代替某些 \(\lambda\) 项，在进行操作语义（化简）的过程中我们可以用符号表示某些 \(\lambda\) 项以图方便

一个注意点是，我们对一个 \(\lambda\) 项进行 \(\alpha\) 等价后，其本质还是同一个\(\lambda\) 项，所以替换的符号是不变的

这一点在化简一个 \(FV \cap BV \neq \empty\) 的表达式时有奇效：

image-20240912095907469

下面这个可以反复做下

image-20240912100112946

函数组合

image-20240912101722158

\(\lambda\) 记法里的 \(f\) 和 \(g\) 不是函数名，其本身就是一个 $\lambda $ 项，和 \(t\)，\(s\) 一样，不要搞混了

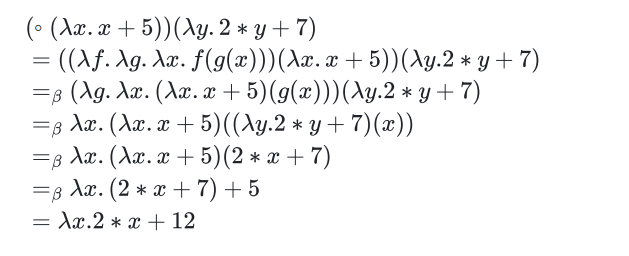
image-20240912102259340

Curring

\(\lambda\) 演算里的所有函数都是只有一个参数的前缀表达式，如果想要一个多参函数，文明可以进行 柯里化，将其转化为多个单参函数

例如双目运算符 \(+\)，对于表达式 \(+12\)，先对双目运算符 \(+\) 应用 \(1\) 得到单目运算符 \(+1\)，在对其应用 \(2\)

image-20240918143034709

总结

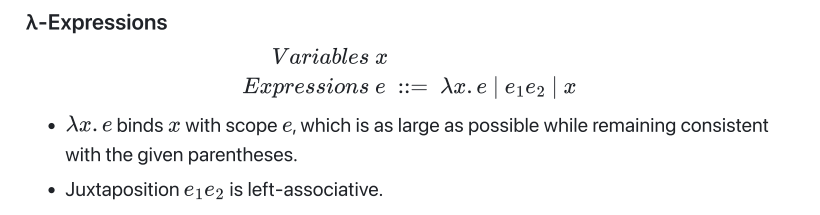
image-20240918143111693

image-20240918143119414

应用

Representing Booleans

定义两个能体现 TRUE 和 FALSE 性质的 \(\lambda\) 表达式，很明显必须是闭项（无自由变量的，独立的，不被上下文影响的），是不可化简的（原子的），

很明显我们可以定义出很多对这样的表达式，下面举个例子

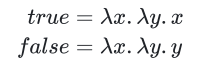
image-20240918143424679

这对表达式将 true 行为规定为取两者中的前者，false 取后者

这里给的例子中，\(true\) 和 \(false\) 是正则的，即原子的/不可化简的

\(not\) 可以被定义为 \(\lambda b.b(false)(true)\)

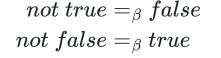
image-20240918144559767

考试就可能给你这个展开后的表达式，让你反推 \(true\) 是什么

再次提醒，这部分所有推断都只是一个例子

\(and\) 也可以记为 \(\lambda a.\lambda b.aba\) ，\(or\) 可以记为 \(\lambda a.\lambda b.aab\)，\(xor\) 可记为 \(\lambda a.\lambda b.a((not)b)b\)

其实就是通过列真值表推断的

Representing Natural Numbers

我们用 \(z\) 代表自然数的起点（不用映射为 \(0\)，就是一个原子的起点），其它自然数都是由其递推出来的

后面略，见1 Lambda(2).pdf P37~41，当练习题

image-20241004115635511