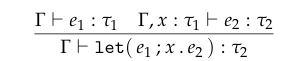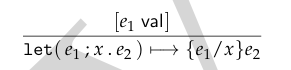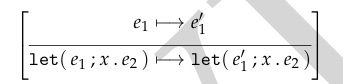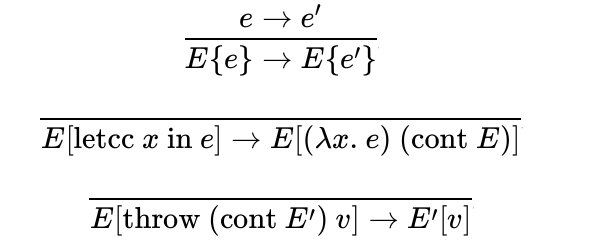PPL HW4
[!ABSTRACT]
3220104929 241126 book.pdf ppl-assignment-4(1).pdf
静态语义和动态语义
[!QUESTION]
Question 1 (2 pts) 代码的编译包括词法分析(将代码分割成若 ⼲ 单词)、语法分析(按照语法,将单词组合成树)、语义分析(表达式中进 ⾏ 类型推断和类型检查等)等步骤,请问其中哪些步骤属于静态阶段?
三者均在代码运行前即可完成,所以均属于静态阶段
[!QUESTION]
Question 2 (2 pts) E 的语法表共 10 ⾏,在这 10 ⾏ 中,哪些是 operator?(你可以使⽤⾏号来回答)
6,7,8,9
let 是变量替换,并非运算
[!QUESTION]
Question 3 (2 pts) 课本通过规则 (4.1) 定义了 E 的静态语义,这⾥需要你简要解释规则 (4.1h) 的含义。
在上下文 Γ 中,变量 x 的类型并没被声明
如果在上下文 Γ 下,表达式 \(e_1\) 的类型是 \(\tau_1\),且已知 \(x\) 的类型也是 \(\tau_1\) 的情况下可以确定表达式 \(e_2\) 的类型为 \(\tau_2\)
则我们可以推断,在上下文 Γ 下,将表达式 \(e_2\) 中的变量 \(x\) 替换为表达式 \(e_1\),新的表达式类型不变
就是将一个表达式里的变量替换为与变量同类型的表达式,整个表达式类型不变
[!QUESTION]
Question 4 (2 pts) 请简要解释规则 (5.4h) 的含义。请注意规则中含有的⽅括号,这也是需要解释的主要部分。
方括号表示条件,用于限制规则的适用性,只有当 \(e_1\) 已经是值时,才能直接应用此规则
如果 \(e_1\) 还未求值,需要先对 \(e_1\) 进行求值,例如
let(2 + 3; x. x + 1)需要先计算2 + 3的结果5,然后再应用规则
\(e_1\) val 的含义是 \(e_1\) 是一个值
如果 \(e_1\) 已经是一个值(即满足 [\(e_1\) val]),那么 let(\(e_1\); \(x.e_2\)) 的求值过程可以转化为用 \(e_1\) 替换 \(e_2\) 中的所有 x
[!QUESTION]
Question 5 (3 pts) 证明......

延续( continuation )
[!QUESTION]
Question 6 (2 pts) 写出延续
[!QUESTION]
Question 7 (6 pts) 规约步骤

[!QUESTION]
Question 8 (5 pts) 规约步骤

全函数与 Gödel's System T
[!QUESTION]
Question 9 (2 pts) 阅读规则 (8.2),解释
在形如 \(apply{f}(e′)\) 的函数应用中才会出现函数名 \(f\),
而 \(e_1\) 可能会调用 \(f\),如果直接用 \(e_1\) 可能会导致结果依然出现 \(f\),所以需要先将 \(e_1\) 里的 \(f\) 做代换
[!QUESTION]
Question 10 (4 pts)
- 根据语⾔ ED 按值调⽤解释下的结构化动态语义,写出这段代码的运 ⾏ 过程, 在每⼀步注明使⽤的规则
- ED 语⾔是静态作⽤域的还是动态作⽤域的?

- 静态作⽤域
[!QUESTION]
Question 11 (2 pts) “急切解释” 和 “惰性解释” 与我们之前讨论的 “按值调 ⽤” 和 “按名调 ⽤” 有何异同?
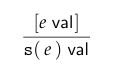
[!NOTE]
急切解释(Eager Evaluation)
- 在急切解释中,
e会被立即计算并简化到一个值- 因此,
s(e)只有在e已经计算为值的情况下才能被认为是值惰性解释(Lazy Evaluation)
- 在惰性解释中,
e并不会立即被计算,只有在实际需要时才会被求值- 由于
e未必需要是值,s(e)的值判断并不依赖于e的立即计算按值解释(by-value interpretation):先求值(保留方括号中内容)
按名解释(by-name interpretation):不求值直接绑定
- 相同之处
- 两类概念都在确定 前提是否需要先计算结果以进行判断
- 不同之处
- 解释适用于讨论所有表达式,调用仅限于讨论函数调用时的参数传递
[!QUESTION]
Question 12 (3 pts) 解释递归式含义
如果 \(e=z\) ,那么结果为 \(e_0\)
否则记 \(e=s(e^\prime)\),调用 \(x.y.e_1\),\(e^\prime\) 绑定至 \(x\),以 \(e^\prime\) 为操作数递归,将结果绑定至 \(y\)
[!question]
Question 13 (5 pts)
- 逐步规约
- 给出两个整数的加法函数