Recursive
:material-circle-edit-outline: 约 430 个字 :material-clock-time-two-outline: 预计阅读时间 1 分钟
全函数 Total function
对于集合 \(A\),一个函数 \(f\) 能作用在 \(A\) 中任意元素上得到结果,那这个 \(f\) 就是 \(A\) 上的全函数
a 输入给 f 能有非空输出,就记作 \(f(a) \downarrow\)
记作 \(f:A\rightarrow B\)
说白了就是函数定义域里面每个元素都有对应的输出,就是我们之前理解的函数
部分函数 Partial function
定义域里部分元素只能得到空集
The Schema of Iteration
\(n\) 次迭代的两种表示方法:

如果某个函数能被表达为上面两种形式,那么其就是一个基于丘奇树的全函数,

例子
下面的乘法是不是递归表达式





后面这段没听到,,,智云重听,PPT 重看
外延性原理
两个函数对任何输入都有一样的输入,那这两个函数就是等价的
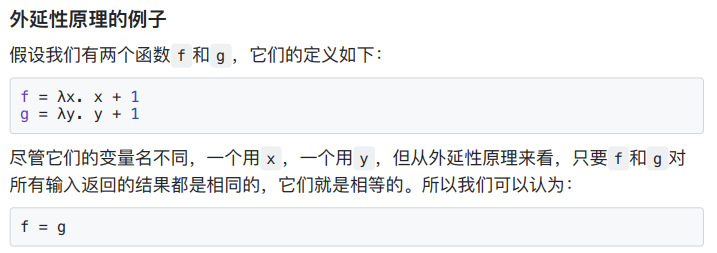
第一章 $\lambda $ 演算已经有各种等价了。。。
原始递归(primitive recursion)

从丘奇递归角度来看,我们第 \(n\) 层的递归是无法知道 \(n\) 是什么玩意儿,因为它的输入值是上一次层递归的返回值,没有输入 \(n\) 这个数

这个 pred 就属于原始递归,即可以输入这个 \(n\),当前递归知道自己在第几层

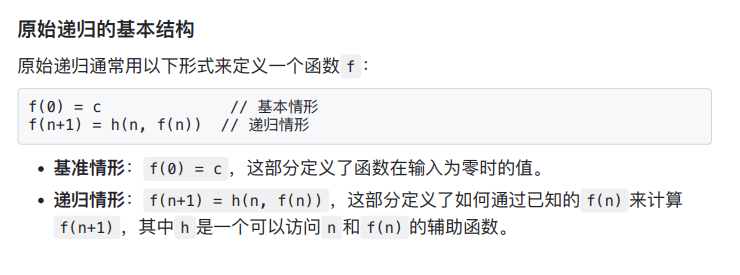
- 特点
- 全函数:原始递归定义的函数总是对所有自然数有效。
- 可构造性:可以通过简单的基本情形和递归步骤来构造复杂的函数。

例子


乘法是丘奇递归,吗?
pair


tmd 就是带入
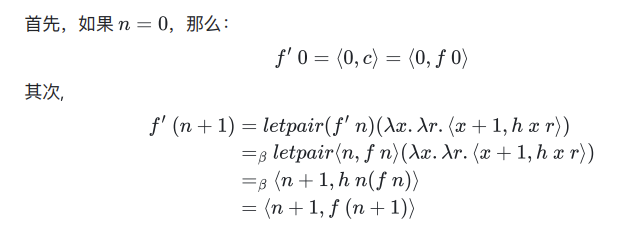

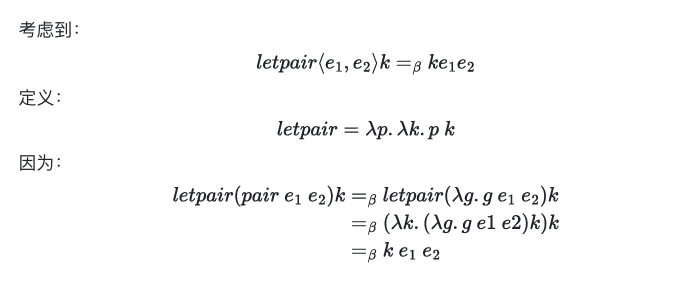
letpair 就是把 pair 里的东西应用于目标

麻,PPT 重新看一遍复习,漏了好多