Simple Types
整数变量放整数,类型变量放类型,前者常用希腊字母,后者常用罗马字母 \(\tau\)
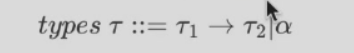
前者是函数的类型,后者是变量的类型
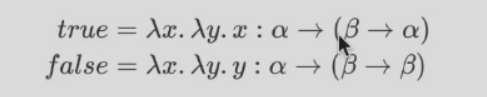
纳尼,true 和 false 类型不一样
谁说 x 和 y 类型不一样
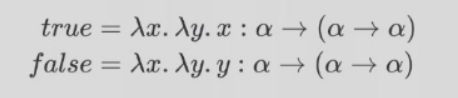
这就是我们布尔量的类型,那是不是这个类型的东西都是布尔量呢?我们之后来看看
类型判断
首先,类型可以推导
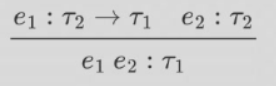
我们用 \(\Gamma\) 记录上下文,也就是所有已出现变量的类型
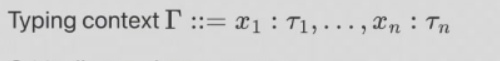
中间这个符号是根据前面的条件推导出后面的结论
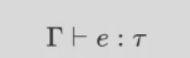

这个意思是,如果 “x的类型是 \(\tau\)” 这个判断包含在 \(\Gamma\),那么废话
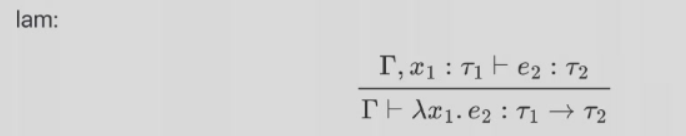
这个是lambda函数
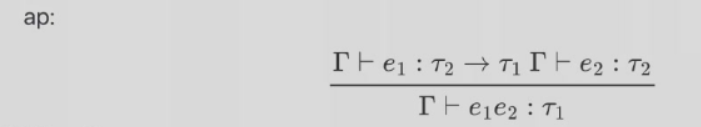
注意第二个 \(\Gamma\) 之前是空格,\(e_1\) 是函数
上面三个是最基本的推导规则
利用规则推导 true 的类型
注意看每一步都是怎么写出来的,其实很简单,但是要知道怎么写
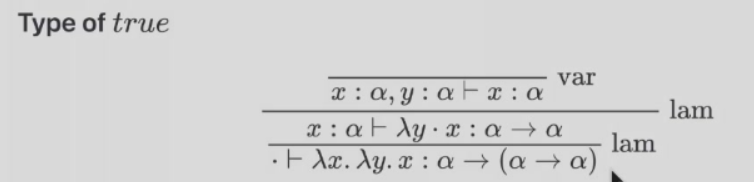
最后一行的最左边有一点,表示已经没有上下文(前提条件)了,或者说左边的东西都到右边了
也就是说,最后的右边部分是无条件成立的
利用规则推导 false 的类型
有一个问题,\(\lambda x.\lambda x.x\) 就是 false,但是比较难判别
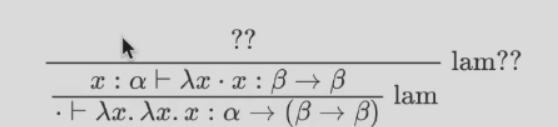
我们可以悄悄地把 \(x\) 改名为 \(x^\prime\)
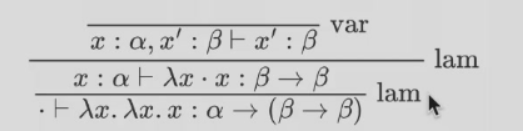
这下完了,true 和 false 的形式好像不止一种,很蛋疼,我们希望只有一个固定的形式
true 和 false 形式唯一化
很明显,上面的类型不一定就是布尔量,但是我们可以限制,例如其可能可以经过规约后变成布尔量
实际上,只要类型符合上面所述的,经过任意次 \(\beta\) 规约后得到的 normal form 就是布尔量
normal form 是指不能再被替换(\(\beta\) 规约)的表达式,也就是终结符
\(\beta\) 规约前后类型是不会变的
类型规约的规则
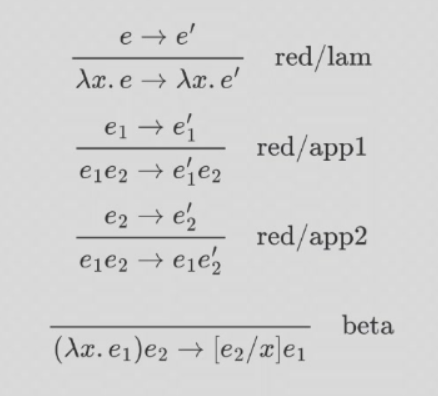
normal form
一个 \(e\) 无法再规约就是 normal form,
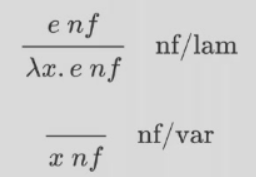
\(nf\) 即 normal form
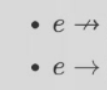
箭头右边不用放东西,这两符号放 \(e\) 后面就是标记 \(e\) 还能不能规约,是不是 nf
积类型
积类型就是PP里的复合类型,比如 C 的 enum 和 struct
二元积
笛卡尔积结果的类型,就一个有序二元组
通过投影进行消去,二选一分量
空积(nullary product)是唯一的无任何值的空元组,类型为 unit
- 惰性动态语义:⽆论分量是否是值,有序对都是值
- 急性动态语义:分量都是值时,有序对才是值
有限积
即 \(n\) 元组

空积与二元积
语法
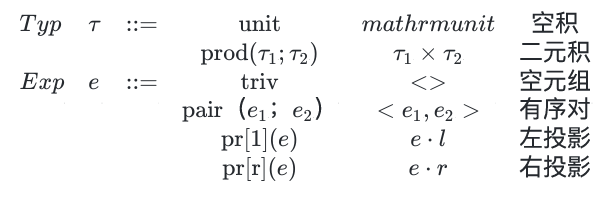
静态语义
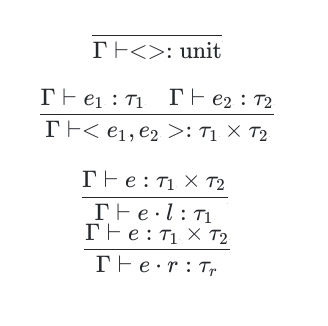
\(\cdot l/r\) 表示左投影/右投影
动态语义
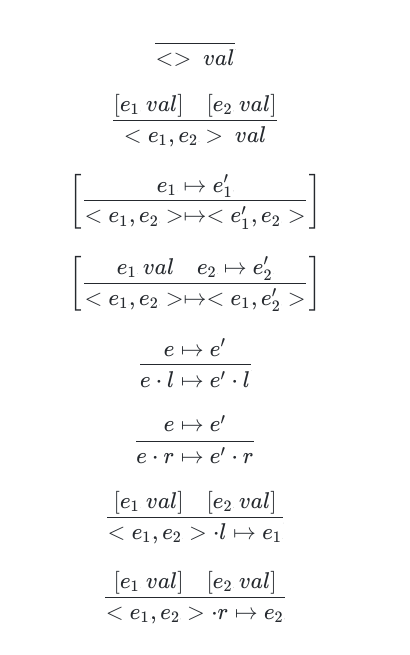
定理10.1:安全性

即,\(e\) 只有两个状态,要么哈可以推,要么推到头了
和类型
空和与二元和
语法

和类型在PL里类似 C 的 enum,里面有很多东西,但用的时候不会同时出现,只能选择其⼀