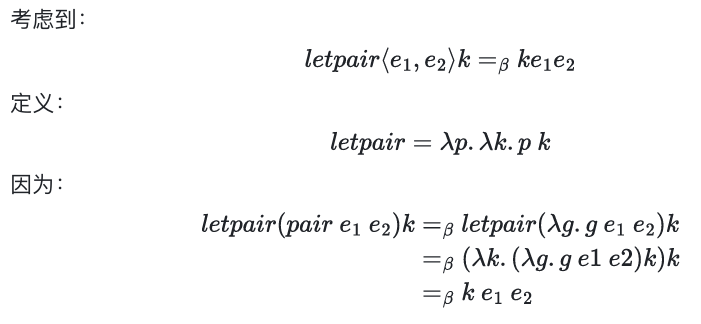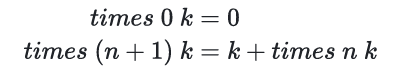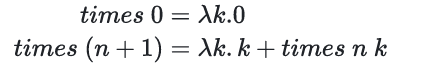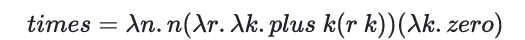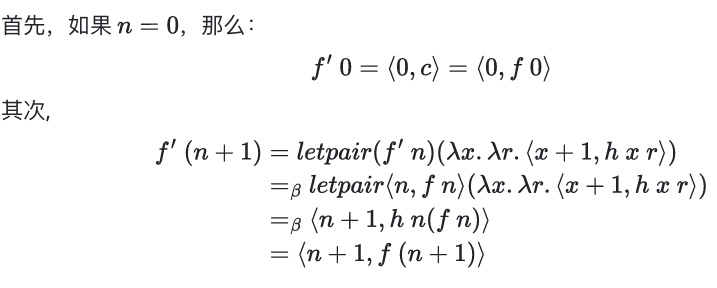Recursive
5 Recursive.pdf 编程语言原理(本)2024-10-23 第 7-8 节
continue our exploration of the λ-calculus and the representation of data and functions on them.
丘奇递归 The Schema of Iteration
丘奇递归
我们用下面形式表示一个递归
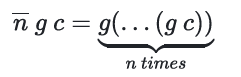
等价于:
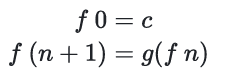
我们称这种形式为 \(\bar{n}\) 的框架,Schema of Iteration
The class of function definable this way is total
[!EXAMPLE]
在函数的递归定义中,除了递归调 ⽤ 的
fn即times nk外,还有额外的参数k这意味着函数不仅依赖于递归结果,还依赖于一个外部的固定参数
通常这样的外部参数是可以存在于递归计算中的
但是为了维持递归的纯洁性,可以抽象和函数化参数
k,让它更符合原始的递归定义
抽象化 k:把 k 变成函数的一个外部参数,⽽ 不是递归函数内部的核心变量
现在这个
times n返回的是一个函数,后者需要再输入 k于是,我们可以用 lambda 表达式这样表示这个递归:
整理后得到最终的
times表达式:
\(n\) 表示对后面的表达式应用 \(n\) 遍,还是挺好理解的,就是注意 \(r\) 传入的是上一轮的结果
柯里化
当一个函数有多个参数时,我们可以使用嵌套的 λ 抽象来定义,将多参数函数分解为多个单参数函数,从 ⽽ 实现灵活的函数调 ⽤
例如,plus = λx. λy. x + y,这 ⾥ 的 plus 是 一 个 “ 柯里化 ” 的函数,即一个多参数函数被拆分成多个一元函数
也就是说,plus 首先是一个接受参数 x 的函数,返回另一个接受参数 y 的函数
如此,我们可以说,plus k 是一个输入一个参数的函数:

Extensionality principle (外延性原理)
函数的定义不 ⼀ 定需要完全 ⼀ 样,只要它们对相同输 ⼊ 的响应是 ⼀ 样的,我们就认为这两个函数是相同的 $$ ∀x, f(x) = g(x) => f = g $$
原始递归( primitive recursion )
前言 pred
pred0 = 0, pred(n+1)= n
我们是无法直接写出 pred 的丘奇递归形式,因为递归形式为 \(f(n+1)=h(n,f(n))\),\(h\) 需要访问 \(n\) 才行,但是传入的是 \(f(n)\)
具体见 5 Recursive.pdf 25-26 页
原始递归
原始递归模式模式如下: $$ f(0) = c\ f(n+1) = h(n, f(n)) $$ \(h\) 是一个新的函数,它不仅接受递归调用的结果 \(f(n)\),还接受当前递归的输 ⼊ 值 \(n\)
对于前驱函数,我们可以定义: $$ pred(0) = 0\ pred(n+1) = h(n, pred(n)),其中 h(n, _) = n $$
特点
全函数:原始递归定义的函数总是对所有 ⾃ 然数有效,是 全函数
可构造性:可以通过简单的基本情形和递归步骤来构造复杂的函数
和丘奇递归的区别就是,递归情形有没有用到 \(n\)
例子
加法函数是一个丘奇递归函数:
$$
add(0, y) = y —— 基本情形\
add(n+1, y) = add(n, y) + 1
——递归情形
$$
乘法函数是一个丘奇递归函数:
$$
times(0, y) = 0
—— 基本情形\
times(n+1, y) = add(y, times(n, y)) —— 递归情形
$$
上面都只用到了上一次的递归结果 \(f(n)\),没有额外用到 \(n\)
pair
积类型的一个特例

letpair 就是专门讲 pair 应用于函数的操作符

lambda 演算联练习:
pair 在 lambda 算子上的定义:

letpair 定义: