PCF 的声明和语法惯用形

:material-circle-edit-outline: 约 747 个字 :fontawesome-solid-code: 4 行代码 :material-clock-time-two-outline: 预计阅读时间 3 分钟

编程语言原理（本）2024-11-20 第 7-8 节 10 PCF 的语法.pdf

编程语言原理（本）2024-11-27 第 7-8 节

let

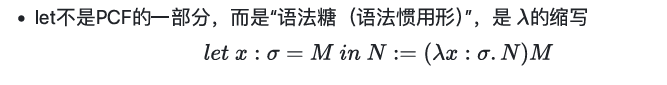
let 就是一个特殊的 lambda 表达式的名字，没有增加 PCF 计算能力

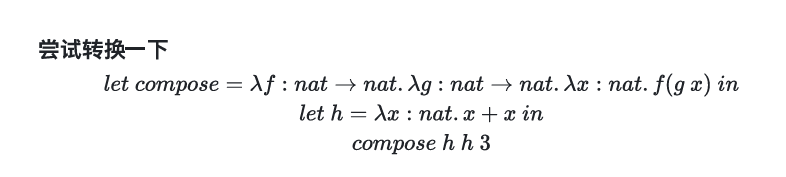
答案是 12

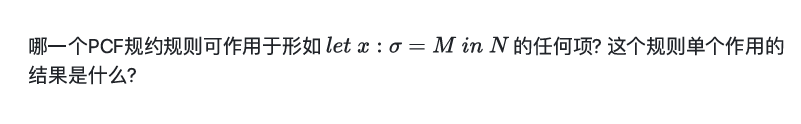
let 规约，把 N 里所有 x 替换为 N

变量查找规则

静态作⽤域（Lexical Scoping）和动态作⽤域（Dynamic Scoping）是两种常⻅的变量查找规则

静态作⽤域

let x:nat=3 in
let f(y:nat):nat = x+y in
let x:nat =4 in
f 5

结果为 3+5 = 8

第二行由于第一行，f 被定义为了 3+y

并因此第三行的操作被无效化了

静态作用域就是在函数定义时给自由变量赋值（编译时就锁死了）

查找变量时，系统从函数或表达式的定义位置开始，沿着代码的作⽤域链向外查找，直到找到匹配的变量。如果找不到，就会抛出⼀个错误。

动态作⽤域

let x:nat=3 in
let f(y:nat):nat = x+y in
let x:nat =4 in
f 5

结果为 4+5 = 9

第三行的操作是有效的

动态作用域就是在函数定义时不给自由变量赋值，根据执行时候自由变量的值来执行（实时更新）

查找变量时，系统根据执⾏时的调⽤栈进⾏查找。也就是说，程序执⾏时，当前函数的外部作⽤域（即它调⽤的函数所在的环境）会决定变量的值

函数计算的范式 normal form

范式：通常指⼀个表达式已经被完全求解，不能再继续简化或者求值

递归终⽌前的每⼀步都是 没有范式 的表达式

T 语⾔是全计算的，类型系统保证计算能够终⽌

PCF 语⾔是部分计算的基础，程序即使是良类型的，计算也 可能不终⽌

我们只需要知道，任意函数都能找到对应的不动点函数

所有这样的算⼦都有不动点，因此这样的等式系统是有解的，这个解由⼀般递归给出，但不能保证为⼀个全函数，使具有数学意义的⽅法就是写出其部分函数的算法

递归定义

letrec ⽤来表示递归定义的变量或函数。与普通的 let 语句不同， letrec 允许在定义过程中使⽤该变量（或函数）本身

letrec f = \x -> x + f(x) in f 5

递归的核⼼就是函数引⽤⾃⼰

不动点算子

不动点算⼦ 的作⽤是对⼀个函数 f 寻找⼀个值 x ，使得 f(x)= x

即 x 是该函数的“不动点”。

阶乘的 fix 归约

BNF 表达的 PCF 语法

语法扩展

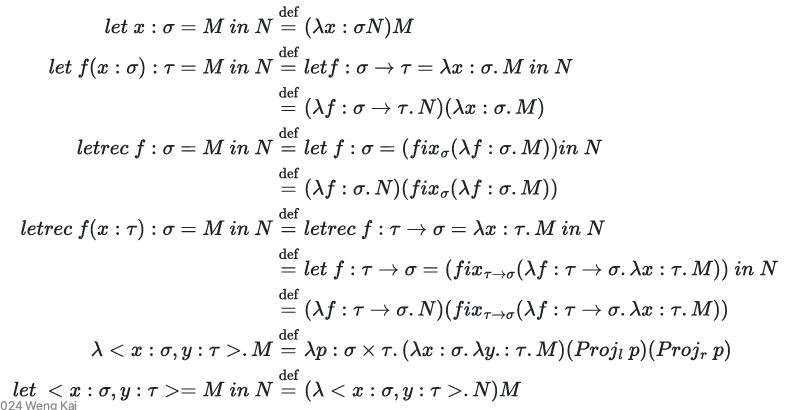
例⼦

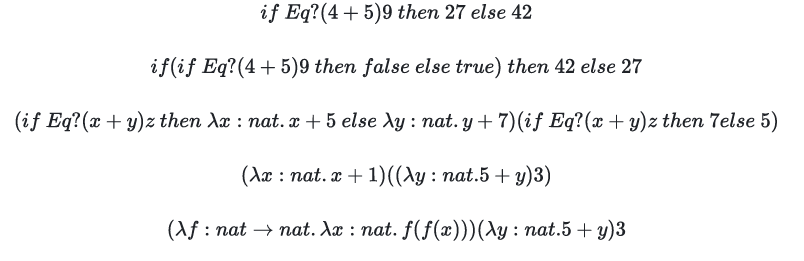
第三行是一个 ap，前面是一个函数，化简的第一步是，把后面那个 if 分别带入前面 if 的两个结果里

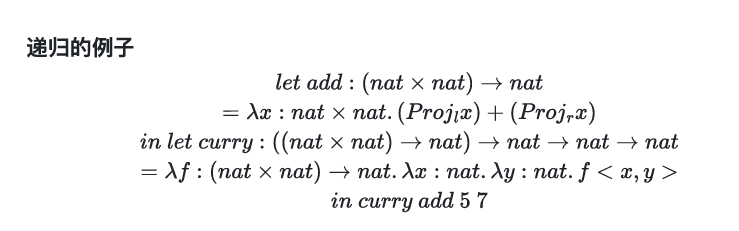
例题

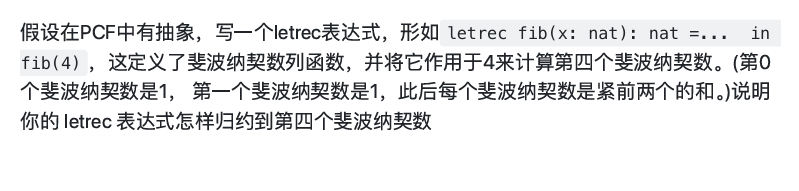
letrec fib(x: nat): nat = 
if Eq? x 0 then 1
else if Eq? x 1 then 1
else fib(x-1) + fib(x-2)
in fib(4)

fib(4)->fib(3)+fib(2)->...->f(1)+...+f(1)+f(0)+...+fib(0)

这题有问题，跳过了