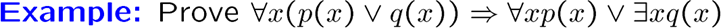Chapter 1 The Foundations: Logic and Proofs
2024.6.1补天ing
离散数学研究的是关系,关系可以表示为 list,matrix,graph
Proposition and Logical Operation
Proposition
命题与逻辑运算符
命题能判断真假,不过不能两个都是
x+1=2 就不是命题,无法判断真假
Logical Operation
-
我们需要五个连接词来描述复合命题
- negation:
¬
- conjunction:
∧,合取符号
- disjunction:
∨,析取符号
- implication:
→
- biconditional:
p ↔ q: p if and only if q≡
- negation:
- 优先级
- 否定优先
- 交并次之
- 推断最后
tautology: 同义反复,即命题的左右式本质上是一样的
还有真值表,学过了
Propositional Formula
我们不能胡乱拼凑原子命题为复合命题,会出现无意义的情况,所以我们需要规定什么是Propositional Formula
我们规定下的命题公式又叫 well formed formula,wff
- 每一个命题变量都是公式
- 两个公式通过上面的五个连接词拼一起,还是公式
- 通过有限次的1,2规则得到的都是公式
公式是可以转化为自然语言的
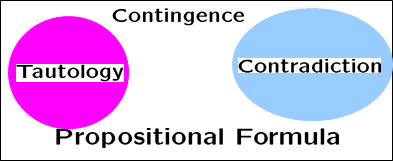
公式的分类
根据公式的真值,我们可以对公式进行分类
- tautology,永真式,例如
p → p ∨ q - contradiction,永假式,一看就懂
- contingence,不是上面两种就是这种
Propositional Equivalence
命题等价
两个命题的 biconditional 是 tautology 的就是等价的
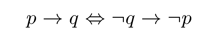
注意,后面我们会学到,我们关于公式的计算规则都是析取和合取的,没有条件和双条件的运算律,所以我们需要全部转化
下面的等价式请记忆
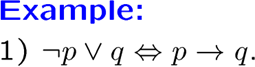
还有一些都快接近公理的运算律,注意到没有条件的,所以公式里有条件就转化!!!

注意结合律只能同类型符号
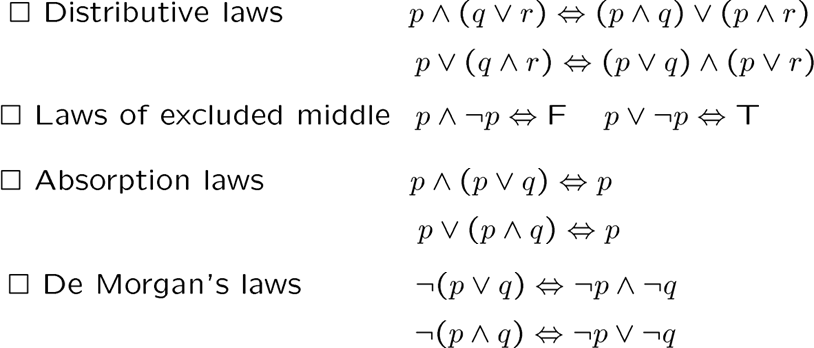
例题
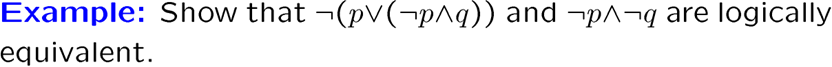
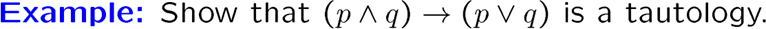
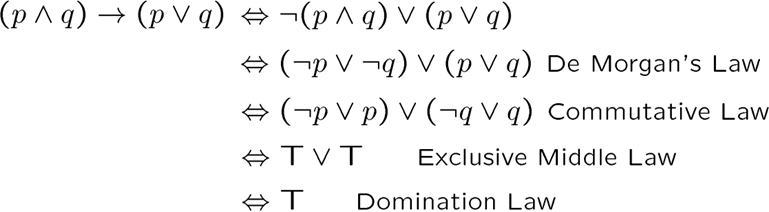
Propositional Normal Forms
任何公式都能转化为下面两种范式:
- 析取范式(disjunctive normal form (DNF)) 先 ∧ 再 ∨
- 合取范式( conjunctive normal form (CNF))
先 ∨ 再 ∧ 。
- 这个我们忽略不学,因为这个表示的是极大项,我们主要考虑极小项
两种范式里面,否定只能放在原子命题上,不能加在公式上
在这里,最小单元叫 literal,包括否定符号和原子命题

由上图可见,这两范式还是不唯一的,我们尝试规定更严格一点,保证范式唯一
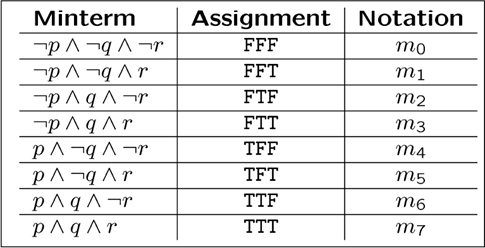
full disjunctive form
又叫 disjunction of mint-erms
就是数逻里真值表转极小项的规则,每个并都要求所有原子命题参与
min-term,又叫 极小项
他吗的原来数逻里的极小项就是这个
- 获取极小值公式步骤
- 先求范式
- 再用双重否定和分配律凑,如下图
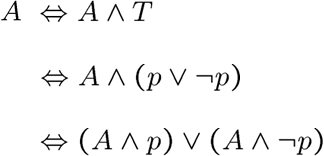

证明理论
- axiom 公理,不证自立
- theorem 定理,可证明
- lemma 可用于证明大定理的小定理
- 。。。
都是很弱智的规则,就省略了,可以看PPT



反证法
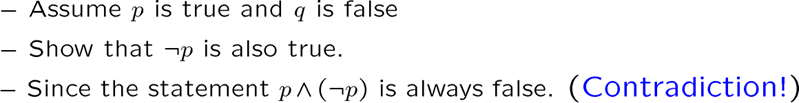
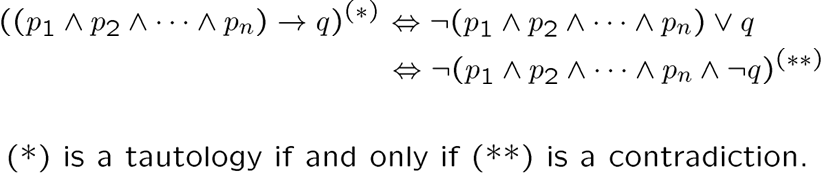
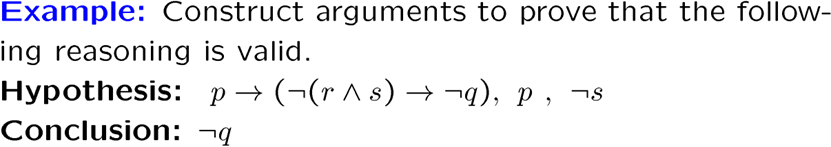

Predicates and Quantifiers
谓词与量词,用于界定 universe of discourse 论域
谓词

就,一个包含未知数的公式,本身不是命题,但是带入未知数的值后就是命题了,这个包含未知数的公式就是一个 Predicate
Predicate 其实是一个布尔函数,取值要么是T要么是F

量词
谓词可以通过量词的量化变成命题,量词为谓语提供了一个范围
一个全称量词,一个存在量词

注意下面例子里谓语的转化

然后谓语和量词不能交换次序,谓语和谓语、量词和量词才可以
更多例子

Banding Varibles
被量词限制的变量就是 Banding Varibles ,是 bound 的,否则就是 free 的
显然存在 free 变量的公式肯定不是命题函数,命题函数的所有变量都应该被 bound
等价谓词公式
下面是一些比较重要的结论
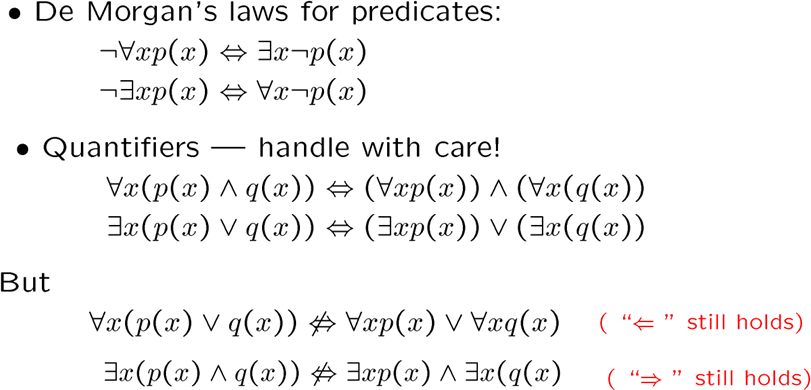

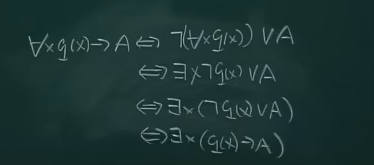
Prenex NF
前缀范式,就是把公式里所有的量词全部放前面

注意全称量词只能在析取时取出,存在量词只能在合取时取出
Methods of proof
牛皮,看这个例题