6

20240604补天ing
最量大管饱的一集
我们学了加法原理、乘法原理,排列组合,可重复排列组合,用构造性的方法运用鸽子洞原理,怎么生成全排列
Recurrence relation
- 递归关系的一些概念
- 一个递归关系基于一个序列,表示这个序列的的任意 term 均可由前面的元素推出来,除了源头
- solution 是满足这个递归关系的序列
- 递归的源头是 initial condition
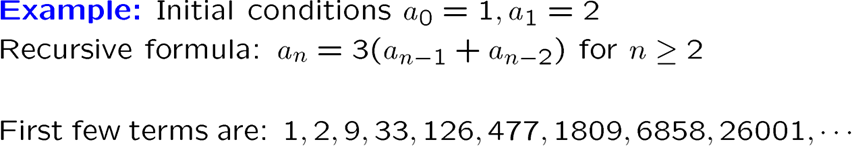
汉诺塔问题

首先,我们需要将最底部的盘子移动到右边最底部,所以肯定得让上面的盘子都移动到中间,是不是有递归的感觉了
记移动次数为 \(H_n\):

例题

就是高中的找递推关系,考试必考

都是很简单的例题,但是第一次做卡住是正常的,啃了一次就有感觉了
用特征方程解递归关系
解递归关系就是解递归方程
常系数线性齐次递归方程
常系数线性齐次递归方程的定义:

注意下面的都不是线性齐次递归方程
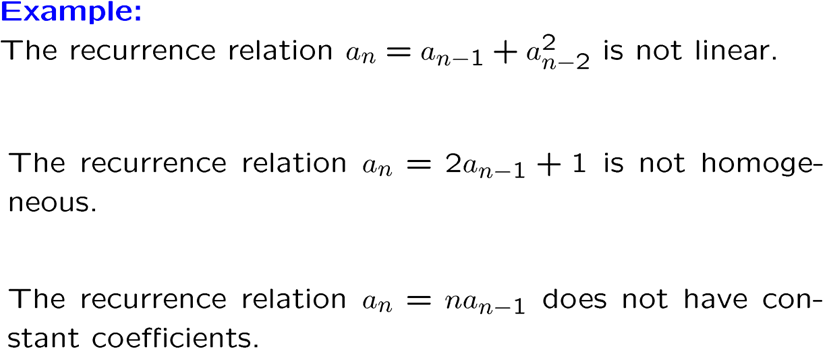
这种形式的方程的解一定是 \(a_n=r^n\) 的形式,其中 \(r\) 是常数,所以我们直接将这个带入原方程,得到 特征方程(character equation),根叫特征根
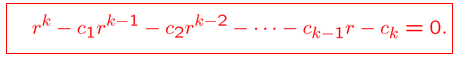
现在变成怎么解这个特征方程,我们根据指数大小来分情况讨论解法
k=2
\(k=2\) 时递归方程为 \(a_n=c_1a_{n-1}+c_2a_{n-2}\), 特征方程只有两个解
如果两个特征根不相等
求出特征解为 \(r_1\) 和 \(r_2\),则递归方程解一定形如 \(a_n=\alpha_1 r_1^n+\alpha_2 r_2^n\),两个 \(\alpha\) 都是常数
证明包括两步,一个是证明 \(\{ a_n=\alpha_1 r_1^n+\alpha_2 r_2^n\}\) 是解,直接带入递归方程即可
还有一个是证明如果 \(\{a_n \}\) 是解,必为\(a_n=\alpha_1 r_1^n+\alpha_2 r_2^n\),证明如下:
这里是待定系数法求出 \(\alpha_1\) 和 \(\alpha_2\) ,然后直接得出结论了,这里不懂啊啊啊啊啊
下面举个例子,请弄清楚每个公式每个变量

斐波拉契数列也可以这样
突然反应过来特征方程的解法高中学过

如果两个特征根相等
解的形式变成 \(a_n=\alpha_1r_0^n+\alpha_2nr_0^n\),就是多乘一个 \(n\),证明方法一样
例题如下

k>2
其实就是有多个特征根,解法都一样
根都不一样


存在相同和不相同的根
乱七八糟的,懒得看定义了


常系数线性非齐次递归方程
常系数线性非齐次递归方程增加了一项 \(F(n)\),不等于0,且只有 \(n\) 一个变量

每一个非齐次递归关系都有一个对应的齐次递归关系

意思是,\(\{ a_n^{(p)}\}\) 是非齐次递归关系的一个特殊解(猜出来的),这个特殊解加上对应的齐次递归关系的解就是通用解
死去的线性代数开始攻击我
例题:


如果 \(F(n)\) 满足下面这个形式,我们又可以讨论一下这时的解的形式

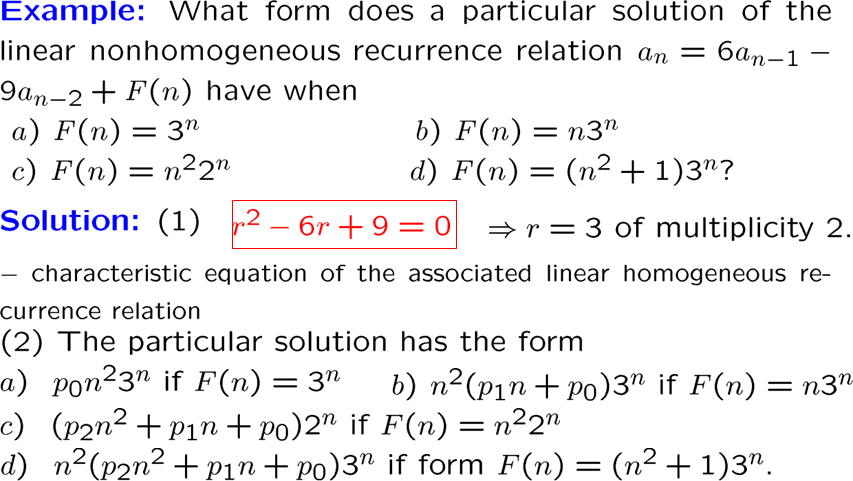
用生成函数解递归关系
什么是生成函数
上面的特征方程虽然是线性代数的方法,但是高中其实都学过了
我们接下来通过生成函数使用微积分求解递归关系
我们首先讨论的,是然后将一个序列转化为对应的函数,如何将一个函数转化为对应的序列
每个序列都有一个对应的生成函数,表示这个函数生成于这个序列,下面是其中一种生成函数的展开式,叫 formal power series ,注意这个式子收敛到的函数才是生成函数

序列的值作为这个模板函数的因数,无限序列可以直接表示成幂级数
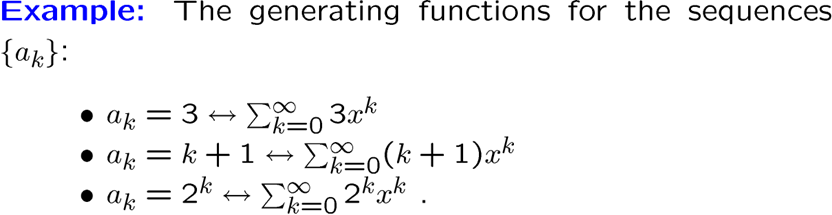
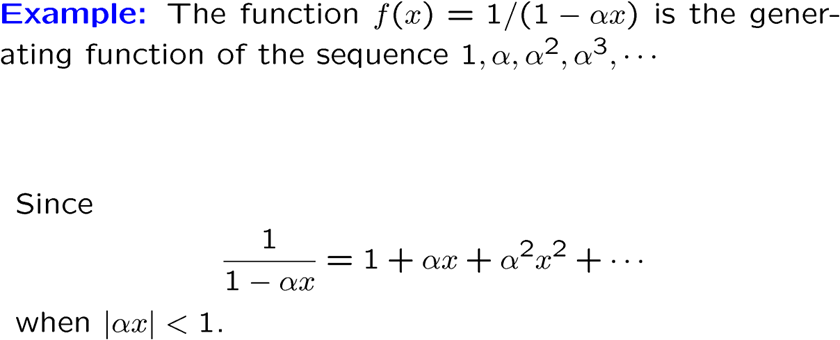
死去的级数开始攻击我
从此,我们的无限序列都可以表示为幂级数了,复习一下幂级数的基本性质
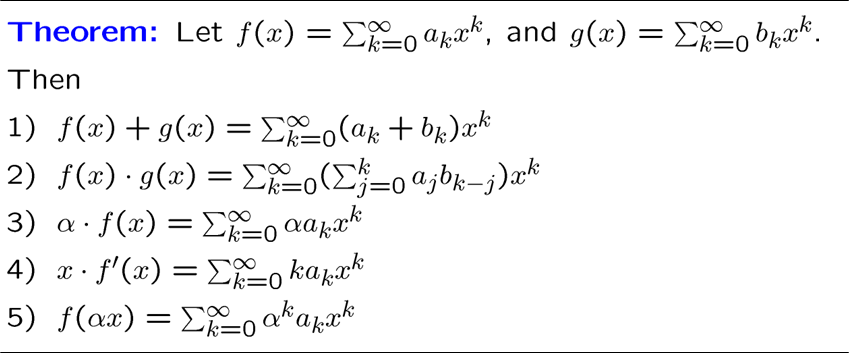
第二个其实就是卷积
什么是卷积:
卷积计算——1. 关于卷积的基本概念_卷积算子-CSDN博客
【CNN】很详细的讲解什么以及为什么是卷积(Convolution)!-腾讯云开发者社区-腾讯云 (tencent.com)
一堆例题
现在我们现在学习的任务就是,根据生成函数求对应的序列,根据序列求生成函数
或者说是,泰勒展开和级数的收敛运算

这个平方可以变成两个相乘,用卷积搞定
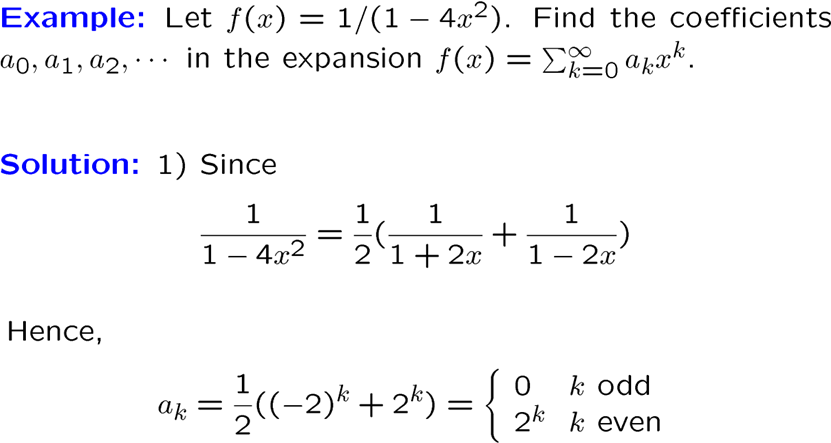
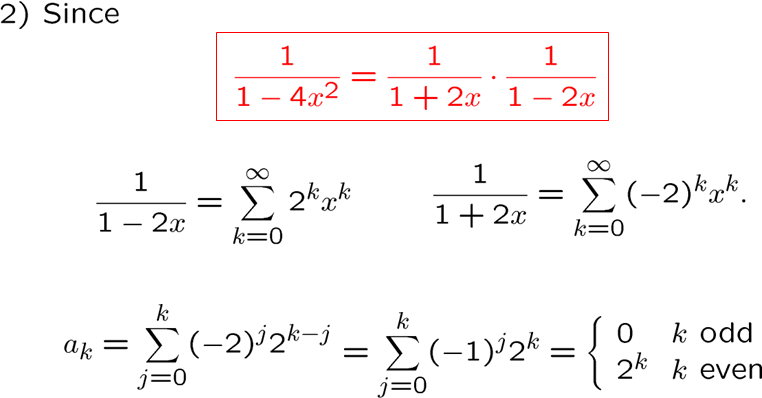
一种看成和,一种看成积
下面通过序列求函数

广义二项式形式的生成函数
广义二项式系数
注意 \(u\) 的取值范围是实数

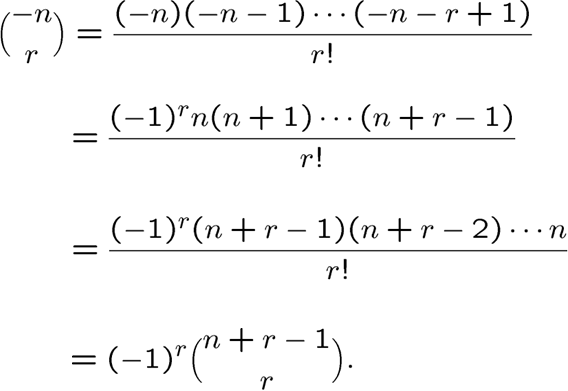
广义二项式系数的运用
于是,\(u>0\) 时我们得到的就是多项式展开表达式,实际上是一个泰勒展开
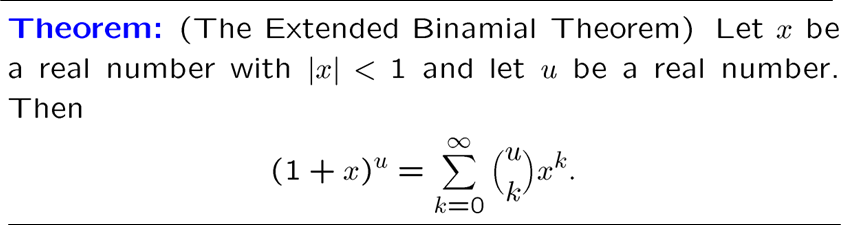
\(u<0\) 时,我们可以得到两个新的等式
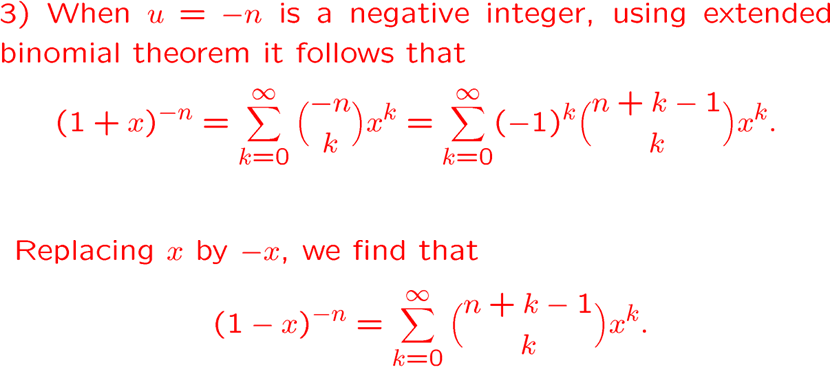
生成函数表

熟悉的级数表
用生成函数解递归方程
下面的例题过一遍,看下具体是怎么操作的


上面这题看起来是杀鸡用牛刀,主要还是初始化一下思路,看下是怎么通过递归方程得到生成函数,怎么展开生成函数,进而由生成函数得序列
下面是更实际的例题,这个是线性非齐次,可以直接用特征方程解,当然我们这里还是用生成函数试试

递归方程用同样的讨论转化为生成函数
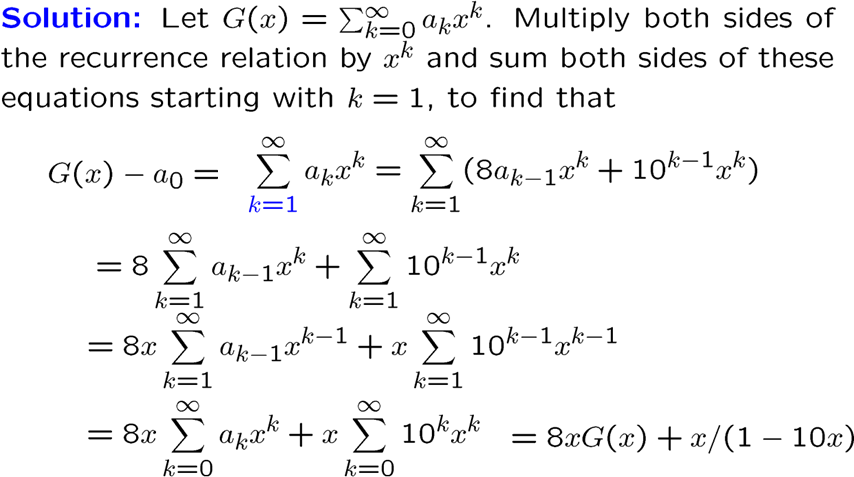
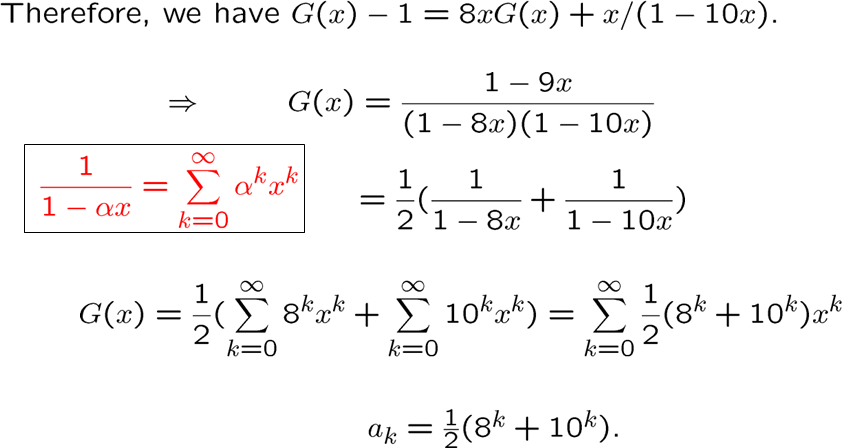
其实这些题目主要还是考变化的数学功底,学的识只是概念和思路
用生成函数解计数问题
我们之前学过的解计数问题的工具有加法原理,乘法原理,隔板之类的
我们接下来试试生成函数来计数
学这部分前,请先回顾多项式展开式怎么求某个特定项的系数
用生成函数做组合
这一块完全不懂
我们找个切入点,先看看 \(\{C(n,k)\}\) 的生成函数
二项式展开可以看成是 \(n\) 个 \((1+x)\) 相乘,我们可以将每个 \((1+x)\) 都看成一个因子,要么取 \(1\),要么取 \(x\),我们可以通过这些因子构造生成函数

我们再看看 \(\{C(n+r-1,r)\}\) 的生成函数
下面这个生成函数就是组合用到的生成函数,牢记


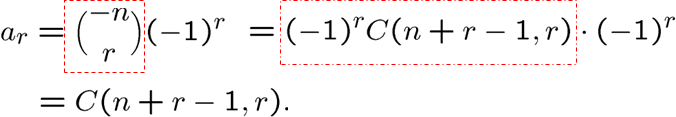
例题

就看这个多项式乘积里面, \(x^{17}\) 这项的系数是多少,这就是答案

同上


没搞懂为什么要变量替换
哦哦,r得从n开始,因为题目规定
我们用函数模型计数,从几类当中选几个,多少类就是几个因子,多少个就是乘幂来定义,最后算对应的系数,完成
用生成函数做排列
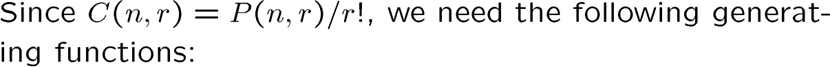
我们需要改进我们的生成函数,满足组合数的关系,下面是我们用到的指数型生成函数

其它都和组合的做法一样
例题
记得先看是排列问题还是组合问题


5个因子,分类讨论,分别构造生成函数

本关考验你的数学分析能力
计数问题这里没搞懂的是为什么可以这样,再看看
容错原理的应用
容错原理
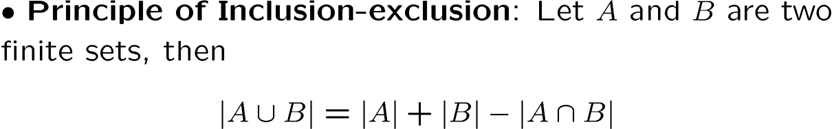
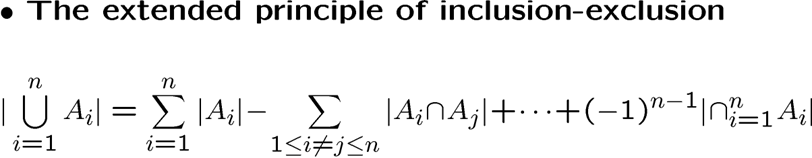
容错原理还可以有另一种形式,从性质角度出发

这种形式是我们接下来采用的
用容错原理解决计数问题
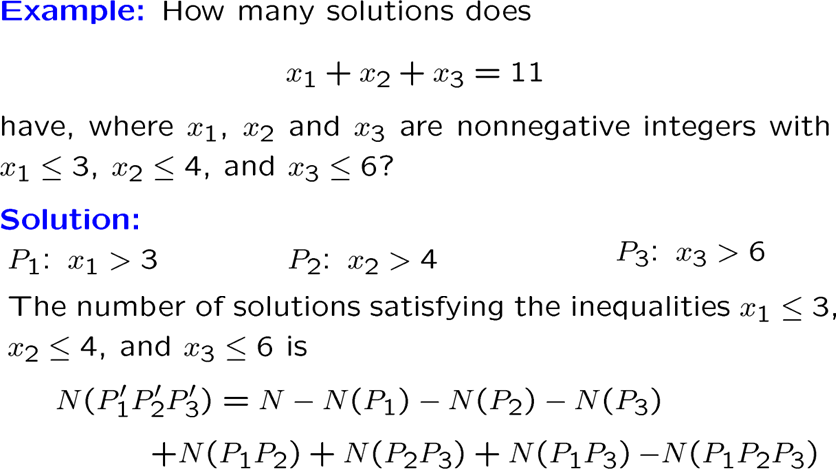


这些N怎么算的没搞懂
用容错原理解决满映射个数问题
满映射英文为 onto function
我们想看看两个集合之间存在多少个满映射

例题

思路就是总的减去P1没被映到的减去P2没被映到的减去P3没被映到的