7

20240605补天ing PPT 离散数学2024-05-10第3-5节 (zju.edu.cn)
我们目前讲完了下面的两个,现在开始学中间的 relation,计算机里面最重要的就是关系
关系定义
用集合表示二元关系,就是两个集合的笛卡儿积的某个子集

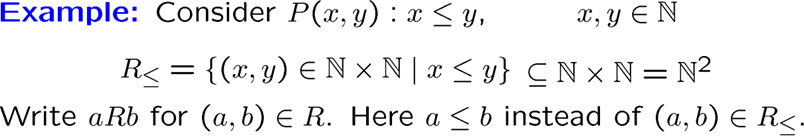
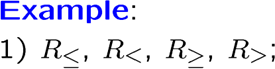
集合上的关系有一种特殊的,叫恒等关系:
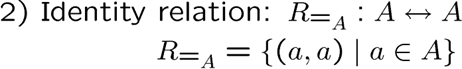
还有整除关系,空关系,完全关系:

关系存在定义域和值域
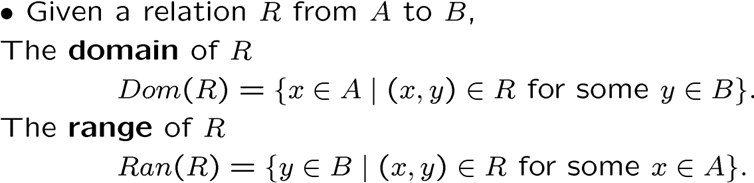
函数是关系,关系不一定是关系,前者要求定义域占满整个集合
关系运算
二元关系其实就是带结构的序偶集合,所以集合运算规则可以用于关系,比如交并补差
有一个新的运算叫 合成(composite):
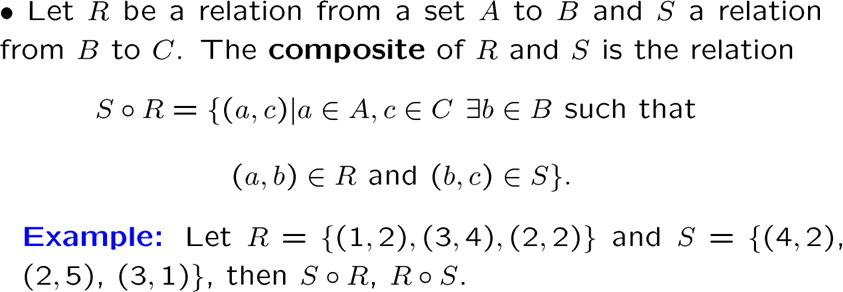
通过合成,我们可以得到乘幂关系:
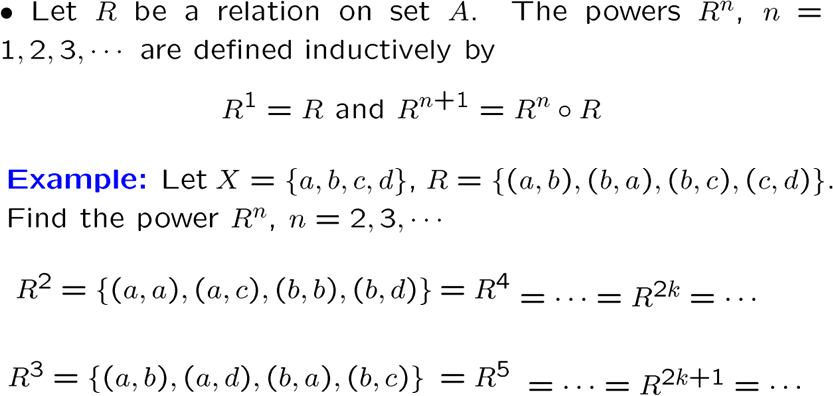
逆关系:

关系性质
自反与反自
自反性质,就是任意输入存在与输入一致的输出
反自性质,就是任意输入不存在与输入一致的输出
注意不自反不等于反自
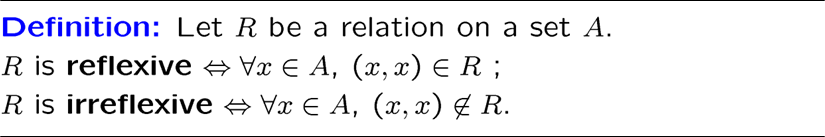

R1是自反,R2是反自,R3既不自反也不反自
我们看看一个集合存在多少个自反的二元关系
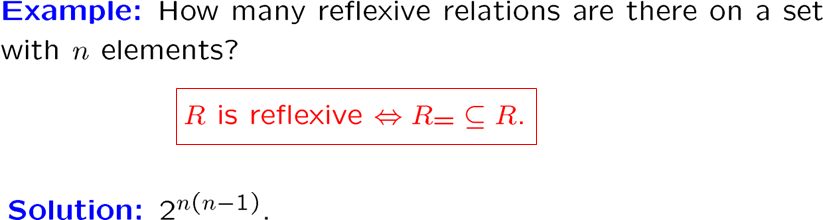
就是笛卡尔积后去掉n
感觉有问题,但没时间想了
反自关系一样
对称与反对称
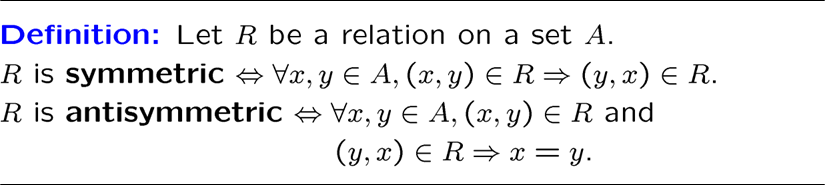
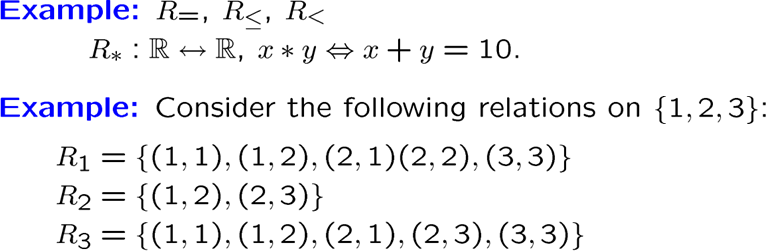
R3既不对称也不反对称,恒等关系既对称又非对称
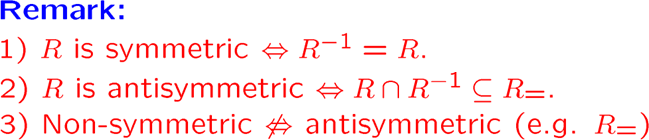

传递性
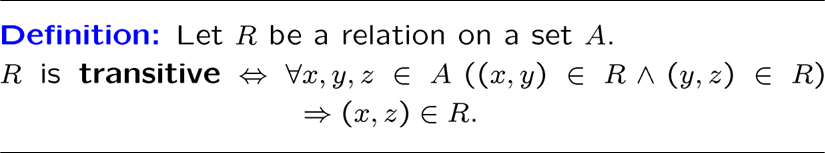
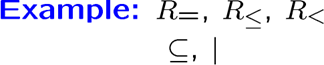
上面几个都是传递关系
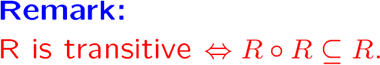
我们可以得到一个结论:

关系表达
有向图本来就可以用关系矩阵表示。。。
关系矩阵
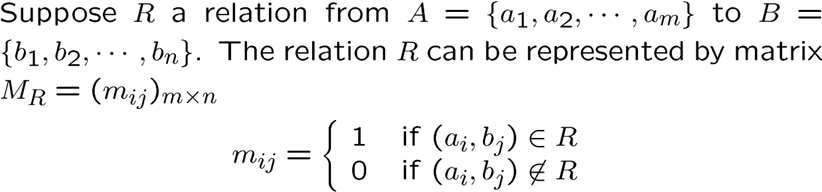
注意起始点对应行
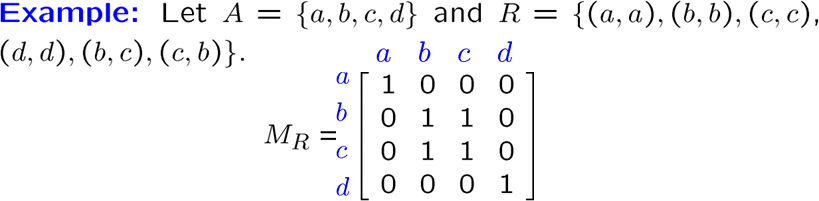
我们来看怎么用关系矩阵表示关系性质:

自反就要求对角线全为1,对称就要求是对称矩阵
传递性比较麻烦,需要计算来验证

我们来看怎么用关系矩阵表示关系运算:

关系矩阵乘法用合取,加法用析取

有向图
有向图英文是 directed graphs/digraph
集合里的每个元素表示为一个结点,结点之间有关系就加一个有向边,组成有向图 \(G=(V,E)\)
有向边表示为 \((a,b)\) ,就是序偶,\(a\) 叫 initial vertex,\(b\) 叫 terminal vertex,形如 \((a,a)\) 的有向边叫环 loop
我们看怎么用有向图表示关系性质:

自反就是每个结点都有环,对称就是有向边是一对一对存在的
关系闭包
就是数据库学过的closure
一个闭包就是一个关系在某个性质上的最小拓展

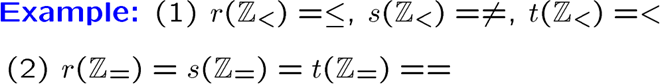
上面的 \(r\) 表示基于自反的闭包,\(s\) 是对称,\(t\) 是传递
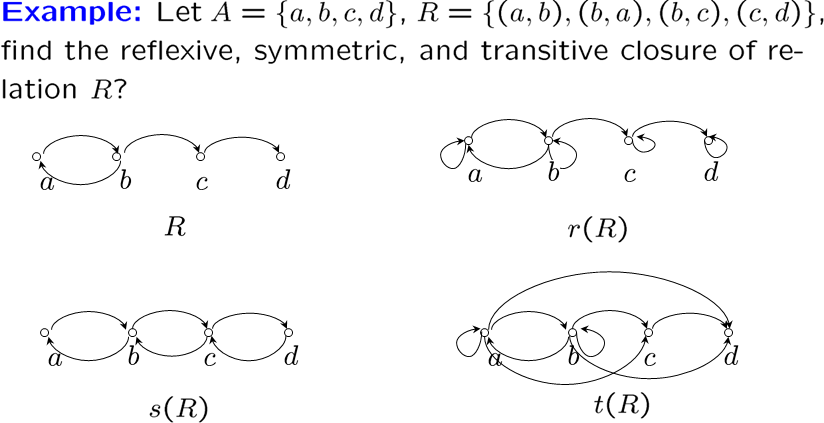
计算闭包
挺直观的:

证明上课讲过,这里略
传递闭包比较麻烦,首先我们需要了解图论里的道路:

我们有结论:\(R\) 的有向图有长度为 \(n\) 的从a到b的道路 iff \((a,b)\) 属于 \(R\) 的 \(n\) 次合成
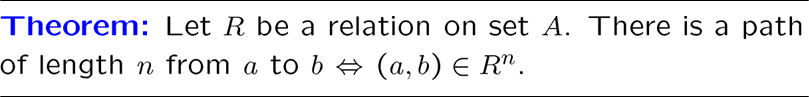
这不废话,当然严格证明可用归纳法
我们再定义一个所谓的连通性关系 \(R^*\),其囊括 \(R\) 所有可组成道路的序偶
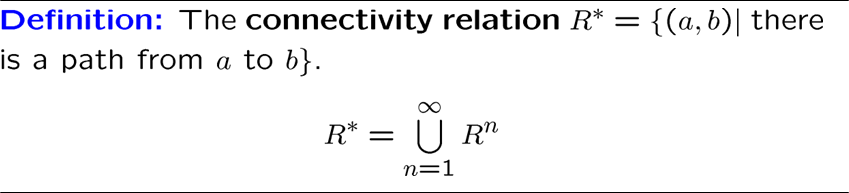
终于,我们可以表示基于传递性的闭包了:

证明略,见PPT27页
可见,我们求传递性闭包实际上就是求连通性关系,所以我接下来看看 \(R^*\) 怎么求
传递性闭包(连通性关系)算法
上面都是无限集,我们算法只能用于有限集,所以需要限制一下
首先需要一个引理:
- 集合 \(A\) 有 \(n\) 个元素,关系 \(R\) 基于 \(A\)
- 如果 \(a\) 和 \(b\) 之间存在道路,那么一定有长度不超过 \(n\) 的道路
- 进一步,如果 \(a \ne b\),那么一定有长度不超过 \(n-1\) 的道路
也是很显然的了,特别长的肯定有重复的元素,我们就去掉所有重复的,保留一个在道路里
有限的连通性关系定义为:
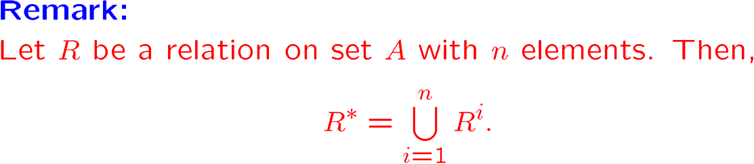
最后给出传递性闭包算法:

0-1矩阵,就是我们上面说的关系矩阵
这算法很好理解,我们的连通性关系是所有 有道路的序偶 的集合,然后幂为 \(n\) 的乘幂矩阵实际上表示的一些序偶,这些序偶拥有长度为 \(n\) 的道路,这算法就是长度从1到n遍历所有道路
如果没搞懂请回去看乘幂与合成的关系
再次强调,对于0-1矩阵,析取等价于乘,合取等价于加,因为操作数只有0和1,结果也只能是这两者
下面是例题

程序描述,附带复杂度分析

⊙是一个逻辑运算符,表示同或运算,即两个输入变量值相同时F=1,或者你可以理解为 两个相同尺寸的矩阵 的 相同位置的元素 相乘,这里用于算乘幂矩阵
很明显,这个算法复杂度很大,我们尝试改进
Warshall's Algorithm
我们上面的算法用的是分类的方式去遍历,接下面我们用松弛的方式,即从有约束条件的情况出发,一点点放宽条件,迭代得到普遍结论
我们关注道路里的内部节点,记为 \(v_1,v_2,v_3,...\) ,为了方便我们一般按矩阵从左到右的顺序
思路就是,先找出所有道路的内部节点只有 \(v_1\) 的序偶,然后允许加入 \(v_2\),以此类推,一步步放宽

- 对于一对序偶,如果其存在只包含前 \(k\) 个结点作为内部节点的道路,那么只可能属于两种情况
- 要么其存在只包含前 \(k-1\) 个结点作为内部节点的道路
- 要么 \(v_k\) 正好能连通两者

由此我们可以确定矩阵每一项该怎么算出来
无脑计算步骤
- 先找到该矩阵的对角线,并从对角线的左上方开始为第一个元素
-
以对角线上第一个元素为中心,按列展开,寻找中心所在的列中所有不为0的元素
-
将“ 该中心所在的行 ”加到“ 该中心所在的列 ”中所有不为0的元素所在的行上
-
加完之后,以对角线上第二个元素为中心,按列展开,寻找该列中所有不为0的元素
-
重复“ 操作3 ”
-
一直到将对角线上所有元素都展开后结束。
还是看例题更容易理解:

\(W_0\) 就是 \(M_R\)


这算法就是fds的 Floyd-Warshall 算法,有向图求所有通道
元素分类
一个关系涉及的元素很多,我们尝试将元素分类,从而分解问题,降维打击
等价关系
等价关系 \(R_\sim\) 是一种特殊的关系,自己和自己组合,且自反对称传递都满足

下面证明同余模是等价关系


等价类
等价类的概念建立于等价关系上,比如上面的同姓关系,你姓张,那你的等价类就是所有姓张的人

等价类表现在有向图上就是等价类内部的任意一对结点都有来回的通道
等价类性质:
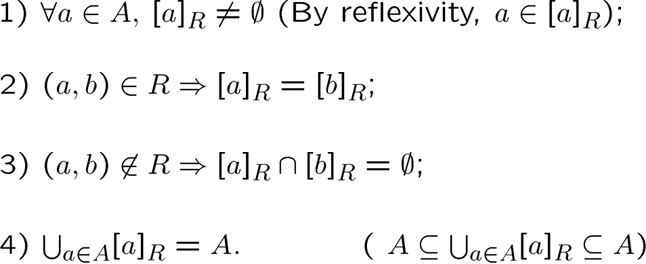
第四条意思是所有的等价类并在一起就是整个集合
所有等价类组成的集合实际上是集合与关系的商
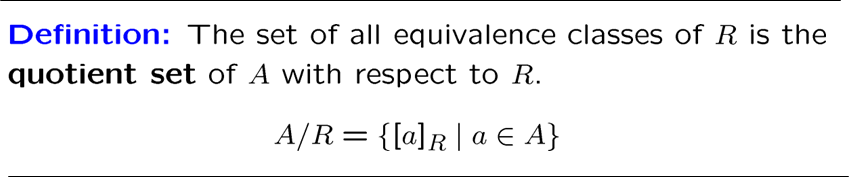
死去的线代二开始攻击我
划分

死去的数分开始攻击我
很明显,一个关系的所有等价类组成了一个关于集合的划分,相对的,对于一个集合的任意划分,我们都能找到对应的等价关系,将该划分的集合作为等价类
偏序(部分次序)
我们给集合内部进行了分类,接下来尝试给集合内部排序
偏序是一种特殊的关系,自己和自己组合,且满足自反、非对称、传递,相应的集合叫偏序集

死去的拓扑排序开始攻击我,拓扑排序就是输入偏序,在保留次序的前提下尽可能改成全序
我们证明整除关系是偏序:

显然同一个集合可以定义不同的关系,比如自然数集我们就有 \(\mathbb{N}_|\) 和 \(\mathbb{N}_\leq\) 两种,而且任意两自然数肯定能比出谁大谁小,却不一定能整除,即 \(\mathbb{N}_|\) 有部分元素对是无法判断次序的,所以才叫偏序
元素 \(a\) 和 \(b\) 之间是能比出谁大谁小的,就叫 comparable,否则就 incomparable
偏序下的大于小于符号如下:
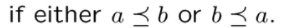


字典序就是一种完全序

哈斯图
我们可以画 hasse diagram 来表现偏序里的次序,画法如下
- 画出偏序的有向图(不要忘了偏序是一个关系)
- 去掉所有的环
- 去掉所有由传递性得到的边
- 起点放下方,终点放上方,边去掉箭头
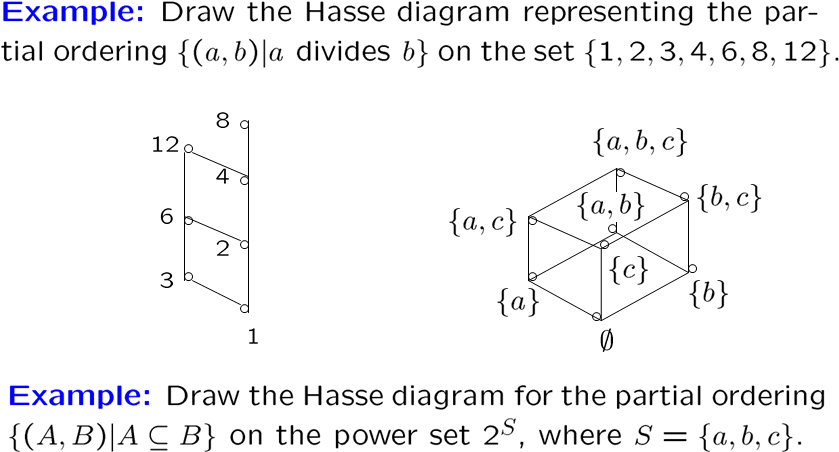
其它相关概念
找不到更大的是极大,比其它任意元素都大是最大,问题就在偏序里面可能存在不能比较的元素,有不能比的就不会有最大的

上界可以不是 \(B\) 里的元素,只要大于等于 \(B\) 里所有元素即可,上确界就是最小的上界

死去的数分一开始攻击我
下面例题好好看看,理解下概念

唯一的极大元是不是最大元?
答案是不能保证,考虑无限集,比如 \(\mathbb{N}_\leq \cup {a}_{(a,a)}\)
良序
任意非空子集都有一个完全序上的最小元的集合就是一个 well-ordered 集,归纳法就得至少良序集才能用

格
一个 lattice 就是偏序集里的一对元素,这对元素既有上确界也有下确界
