8

20240606补天ing PPT 离散数学2024-05-31第3-5节 (zju.edu.cn)
图论,其实fds里代码都全写过一遍的了,主要学学概念
图的分类
无向图
无序偶我们用的是花括号(就是集合),有序偶用的小括号,序偶默认都是有序偶
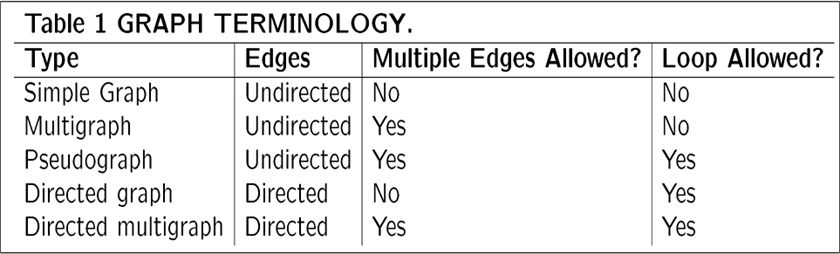
- simple graph 简单图:不同结点才有边,且只能有一条边
- multigraph 多图:不同结点之间可以有多条边,被称为平行边
- pseudograph 伪图:结点自己可以有边(loop)
有向图
有向图都允许有loop
- directed graph :不允许有平行边,注意有向边平行得方向一致
- directed multigraph :允许有平行边
图的术语
无向图
- \(adjacent/neighbor\) 点与点相邻,两个结点相邻表示他们之间有条边
- \(incident\) \(with\) 点与边关联,边与其两端结点有关联,端点又叫 \(endpoint\)
- \(degree\) 度数,一个结点的度数即其有的边
- \(deg_{isolated\;vertex}=0\),孤立点
- \(deg_{pendant\;vertex}=1\),悬挂点
无向图有个握手定理,就是度数和等于边的两倍

有向图
- \(adjacent\) :要求是起点与终点相邻,终点被起点相邻,有方向

度数也有出入两种

注意一个环对两种度都贡献了 \(1\)
有向图也有个握手定理,就是度数和等于边的两倍
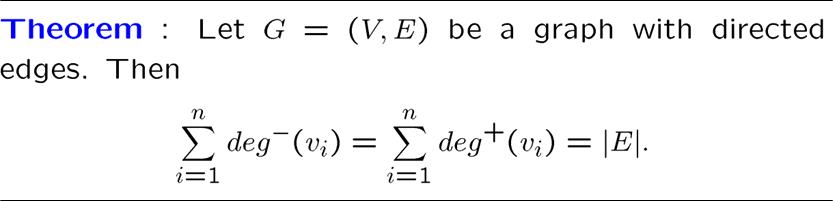
特殊的图

完全图:无向简单图,已经无法增加任何边了,用 \(K_n\) 表示

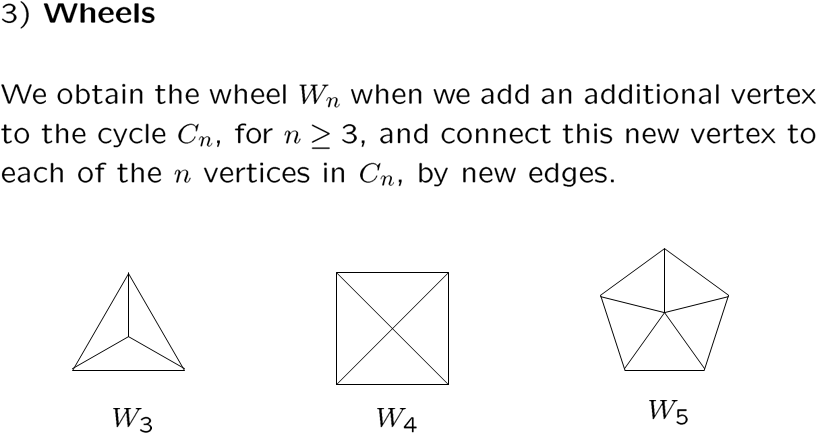
有且只有一个顶点与cycle的所有顶点相连

\(n\) 维立方体,我们知道二维立方体就行了,超立方体没学过
两部图,结点分为两部分,所有边都是跨越这两个部分的,同一部分的顶点之间不存在边
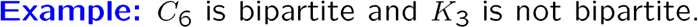
\(C_6\) 两个三角形顶点分别为一组即可
只要图里面含有奇数长度的回路,肯定不是两部图
完全的两部图叫完全两部图,记为 \(K_{m,n}\),\(m\) 和 \(n\) 为两部分各自的度

更多的图
- subgraph 子图:结点和边都是另一个图的子集、即从另一个图中拆分出来的图
- spanning subgraph 生成子图:结点一样多,边是子集
- 简单图的 union :边和点各自并
图的表示与同构(isomorphism)
图的表示
adjacency matrix 邻接矩阵
复习一下,邻接是结点与结点之间的关系
简单图必是 0-1对称矩阵
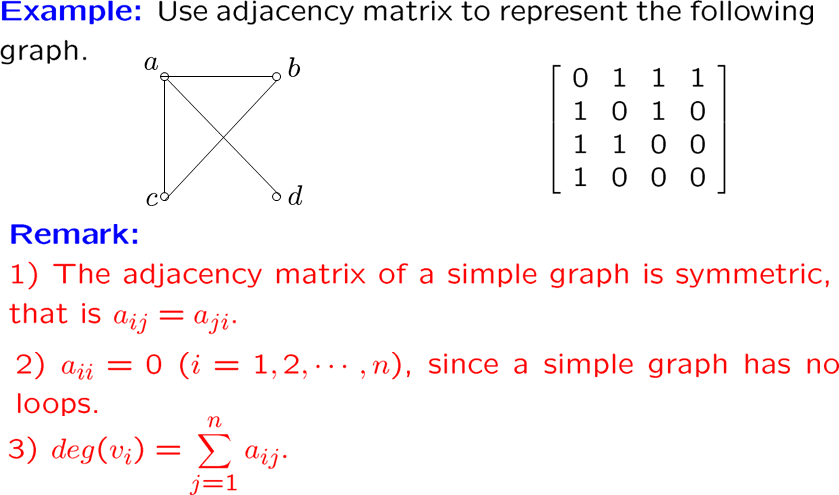
多图和伪图就不是0-1矩阵了,数字表示连接的边数

不过,无向图矩阵都是对称的,有向图就不保证对称了
incidence matrix 关联矩阵
从 点x点 的方阵变成 点x边 的矩阵

一个边只 incidence with 一个点,或者说列向量只有一个1,那就是一个 loop
平行边对应相同的列向量
同构
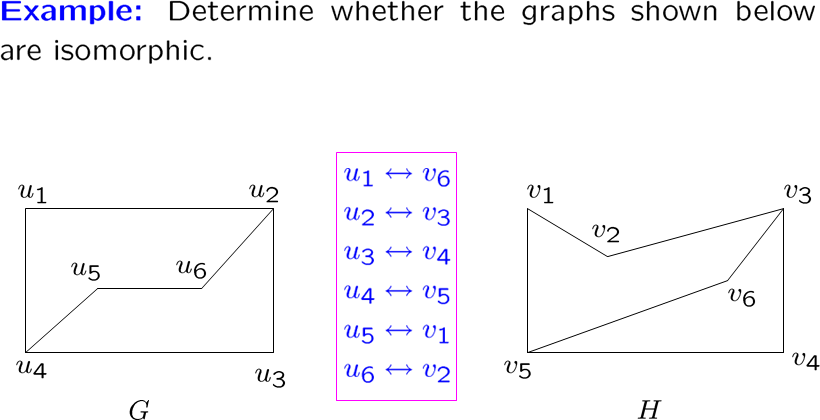
两个图,结点一样多,边一样多,如果能找出一个结点对到结点对的双射,任意一对节点对都有边,那这两个图就是同构的

这个双射也叫同构映射
死去的线代开始攻击我

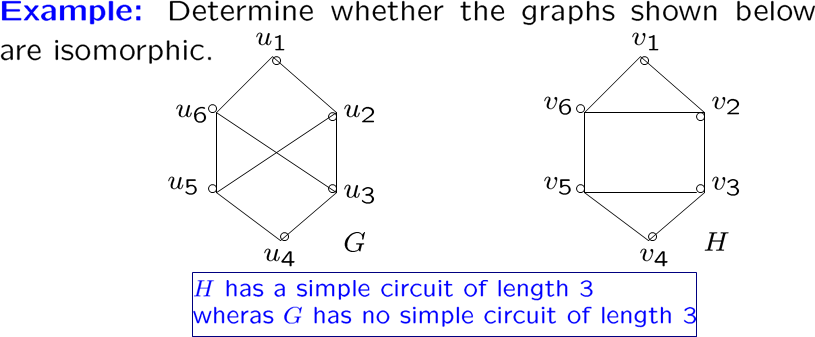
这两个是不同构的,\(G\) 中两度的结点连的都是三度的,\(H\) 中则不是
判断不同构简单,判断同构见fds笔记
离散数学2024-06-07第3-5节 (zju.edu.cn)
连通性概念
无向图
- path 道路,已经讲过了
- circuit 回路是首尾相连的道路
- simple path 是边不重复的道路

多提一嘴,无向图用 \(f(e_1)=\{x_0,x_1\}\) 来描述边
无向图里面,任意两个结点都有道路,这个图就是连通的 (connected)
定理:连通无向图的任意两个顶点必定存在简单道路
有向图
有向图用 \(f(e_1)=(x_0,x_1)\) 来描述边
有向图的 circuit 就是起点与终点一致
其它从无向图类推即可
有向图的连通性强度
在连通的有向图里,任意两顶点都有来回的两条道路就是强连通,否则就是弱连通

注意这两个概念的前提是连通图,第三个根本没连通
cut
不连通的图可以拆分为多个连通的子图,这些子图叫做 connected components
一个连通图里,那些被拿走会产生 connected components 的顶点叫 cut vertices,边则叫做 cut edge / bridge,连通性会下降
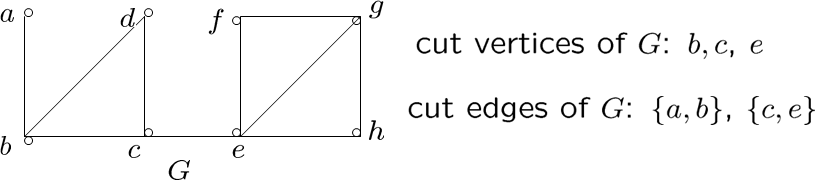
连通性计算
怎么求两个顶点之间长度为 \(r\) 的道路的数量:

类似闭包的计算,可用归纳法证明
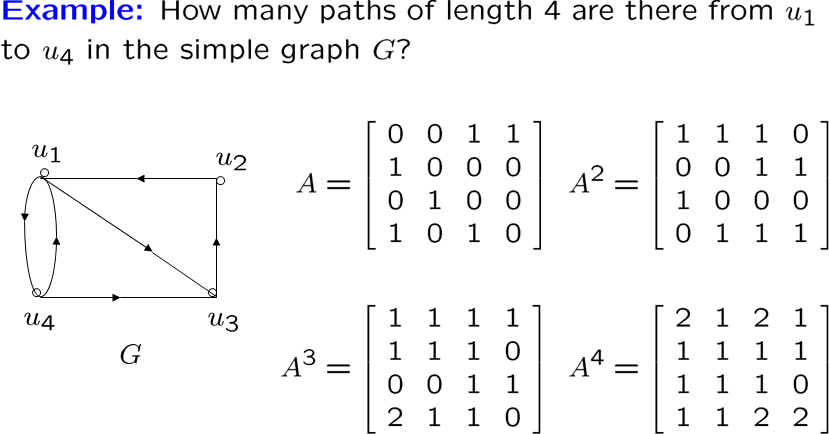
无向图的连通性,只需要算 \(\Sigma A^i\) ,看对角线之外是否全部非0,有一个为0就说明不连通
有向图。。。
道路与同构
回路常用于证明两个图不同构
欧拉图
欧拉回路是一个包含图中所有边的简单回路,欧拉道路是一个包含所有边的简单道路,欧拉图是存在欧拉回路的图
能一笔画回到起点的就是欧拉图
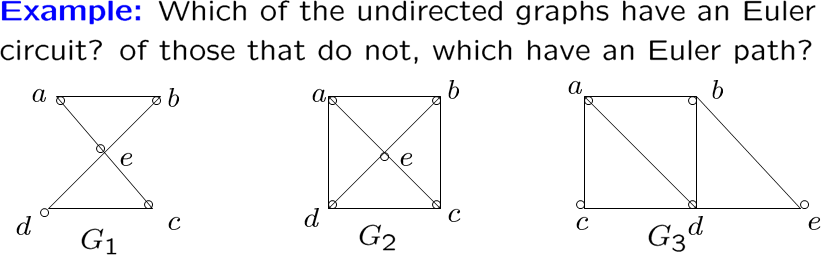
上面第一个是欧拉图,其它不是,第三个只有欧拉道路没有回路
欧拉图的充分必要条件:是连通图,且每个顶点都是偶数度
很显然,每个点都是一进一出,一个点只有奇数条边说明还有没被访问的边
只有欧拉道路、没有欧拉回路的图的充要条件:奇数度的结点有且只有两个
哈密尔顿
哈密尔顿没有充要条件
哈密尔顿道路是一个访问了所有结点结点且均只访问一遍的道路,同理有哈密尔顿回路
一个存在 Hamilton 回路的连通图叫 Hamilton 图

Hamilton 图的充分条件:一个顶点数 \(n\ge3\) 简单连通图,每一个顶点的度 \(\ge n/2\),则这个图是哈密尔顿图
以及,一个有 \(n\) 个结点的简单图,如果任意一对节点的度数之和 \(\ge n\),则这个图是哈密尔顿图
从度数和入手,反证法证明是连通图
先证有哈密尔顿道路再证是一定是回路,都是利用度数
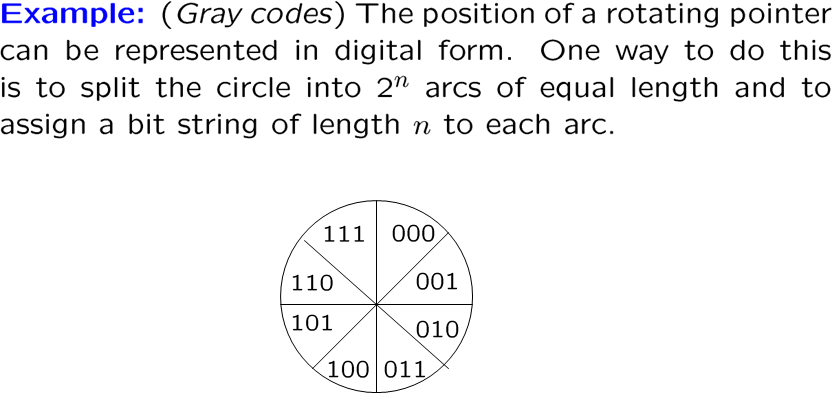
死去的数逻开始攻击我
就是设计状态机
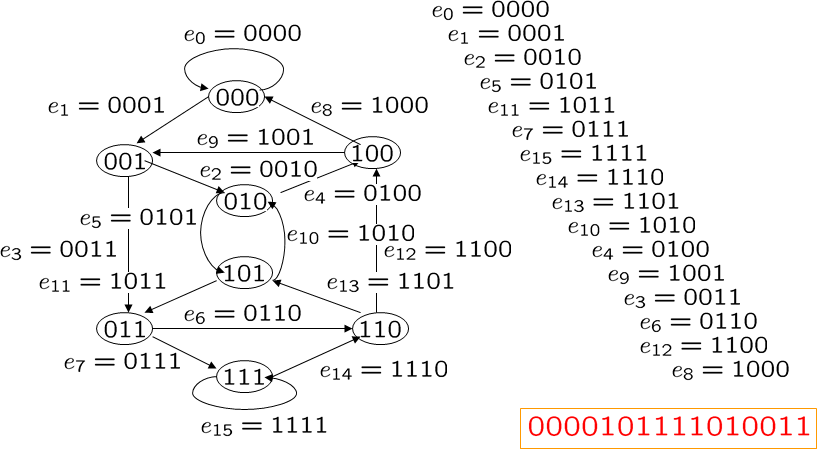
最短路径问题
死去的fds开始攻击我,dijkstra
加权图 (weighted graph) 每条边都有个权重,道路长度为权重和
松弛迭代
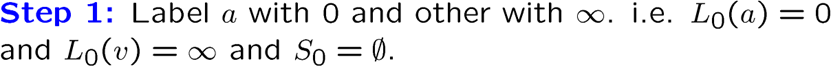
首先将起点距离设置为0,其它为无穷,表示这些边在考虑范围之外,等价于没有与起点相连,然后将起点纳入考虑范围

每轮先更新权值,然后加一个最近的点,需要判断原最短路和原最短路加新结点哪个更小,且需要更新其它点的权值
迭代到包含终点为止

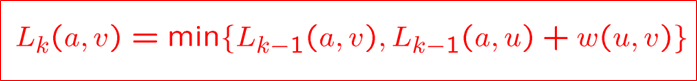
注意权值是起点到这些点的距离,没连上就是无穷大
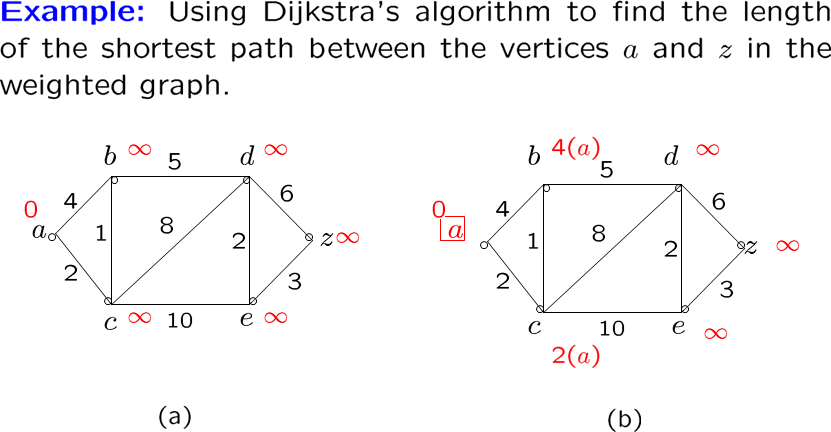
注意是先更新所有可以更新的权值,再加入一个最近的点,上面是第一轮
下面是第二轮和第三轮
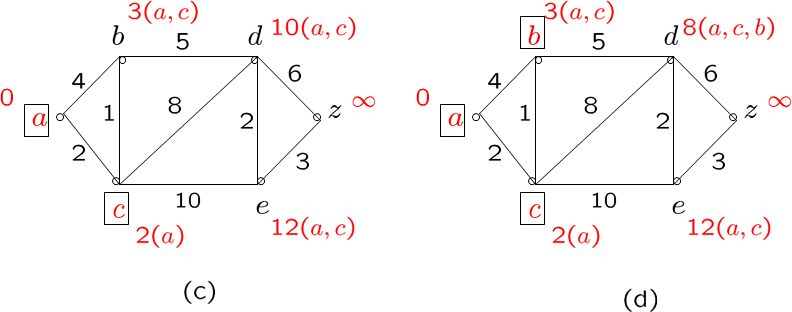
第四轮和第六轮
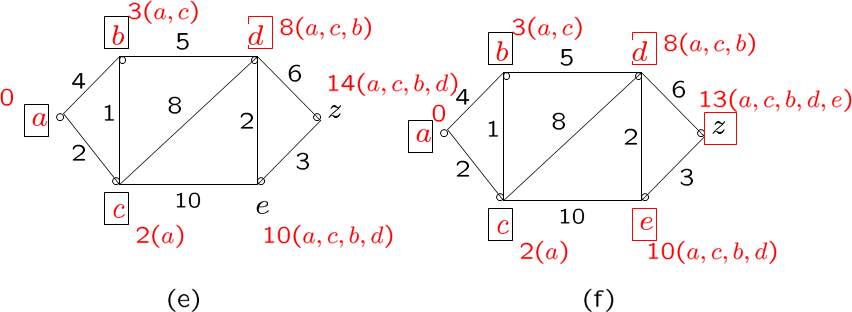
dijkstra算法可以找到加权连通简单图的最短路径,易证
平面图
如果一个图画在平面上,有办法不出现交叉的边,那就是是 planar graph,这么画的图叫原来的图的 planar representation,平面表示
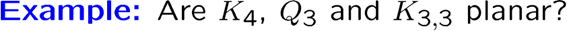
前两个是,\(Q\) 都是平面图,只需要放大其中一面,其它塞进去就行
33两部图不是
一个平面表示可以分为多个区域 region ,其中有无界的
如果一个区域D可以被包含在一个以原点为中心的圆里面,那么称区域D有界,即存在正数M,使区域D内的每个点都满足
无界区域 unbounded 即非有界区域
感觉无界区域很奇怪?注意,一张图的平面表示,不仅包括你看到的一个图形,还包括图形之外的无限的平面区域,这些就是无界区域
欧拉公式
一个连通平面简单图,有 \(e\) 条边,\(v\) 个顶点,\(r\) 个 region,那么有欧拉公式: \(v-e+r=2\)
不是平面图就没有区域概念,更没有欧拉公式
欧拉公式的一个推论 corollary:
一个连通平面简单图,有 \(e\) 条边,\(v\ge 3\) 个顶点,则有 \(e\le3v-6\)
区域的度即区域边界有几条边,显然最少为3,因为一个区域至少要三条边
所有区域度数之和等于 \(2e\)

另个推论 :
一个连通平面简单图,有 \(e\) 条边,\(v\ge 3\) 个顶点,没有长度为3的回路,则则有 \(e\le2v-4\)
即有界区域需要至少4条边才能维持

图的着色
就我们希望用最少的颜色,让任意相邻的区域颜色不同
我们可以转化为图的问题,每个区域看成点,相邻的区域画个边,变成了点的着色
这个新的图叫原来的平面图的对偶图(dual graph),最少的顶点颜色数量叫这个图的 chromatic number
四色理论:平面图的 chromatic number 不大于4
\(K_n\) 显然需要 \(n\) ,\(K_{m,n}\) 一定是 2,\(C_n\) 的 \(n\) 偶数时只需要2,奇数需要3