Skip to content

题目4

:material-circle-edit-outline: 约 276 个字 :material-clock-time-two-outline: 预计阅读时间 1 分钟

解递归关系

特征方程

image-20240604120028762

image-20240604120244680

image-20240604120342405

image-20240604120508876

image-20240604120604734

image-20240604222929336

image-20240604222938278

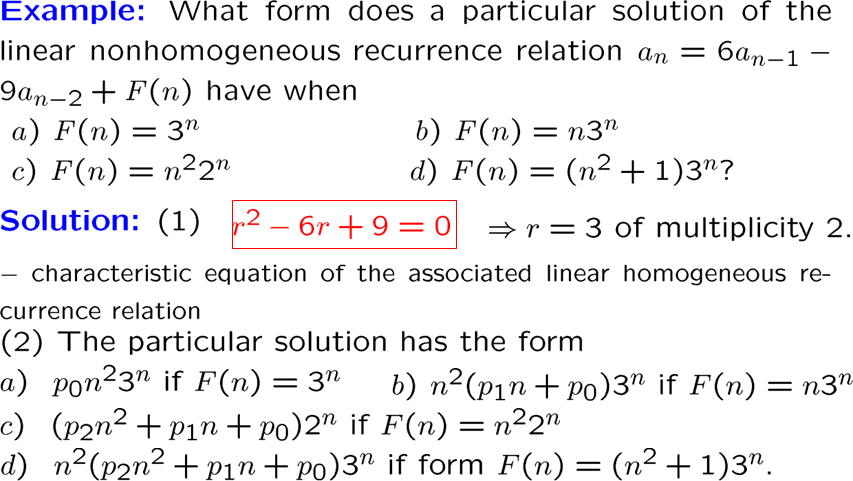
image-20240604223905354

生成函数

image-20240604144103572

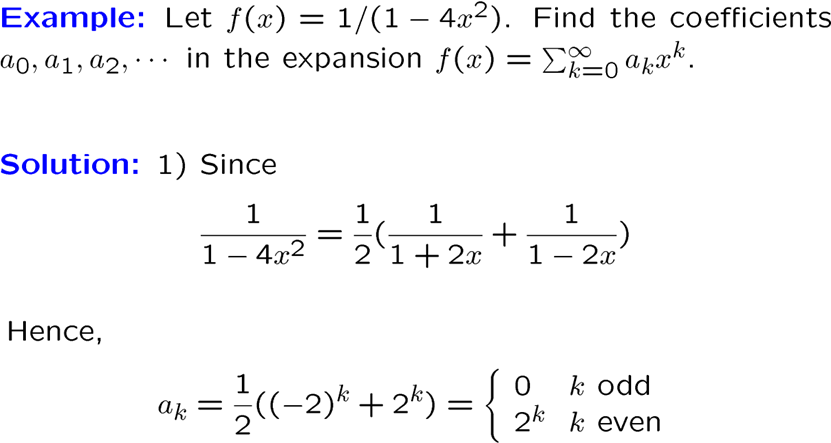
image-20240604144326852

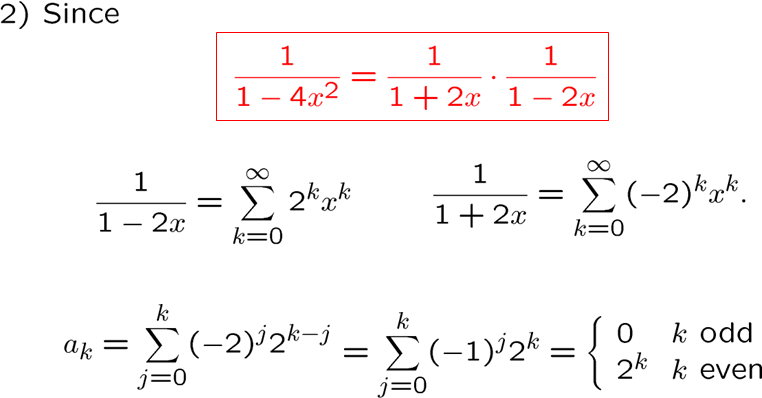
image-20240604144333780

image-20240604144455046

用生成函数解递归方程

image-20240604232200606

image-20240604232458677

上面这题看起来是杀鸡用牛刀，主要还是初始化一下思路，看下是怎么通过递归方程得到生成函数，怎么展开生成函数，进而由生成函数得序列

下面是更实际的例题，这个是线性非齐次，可以直接用特征方程解，当然我们这里还是用生成函数试试

image-20240605092635807

递归方程用同样的讨论转化为生成函数

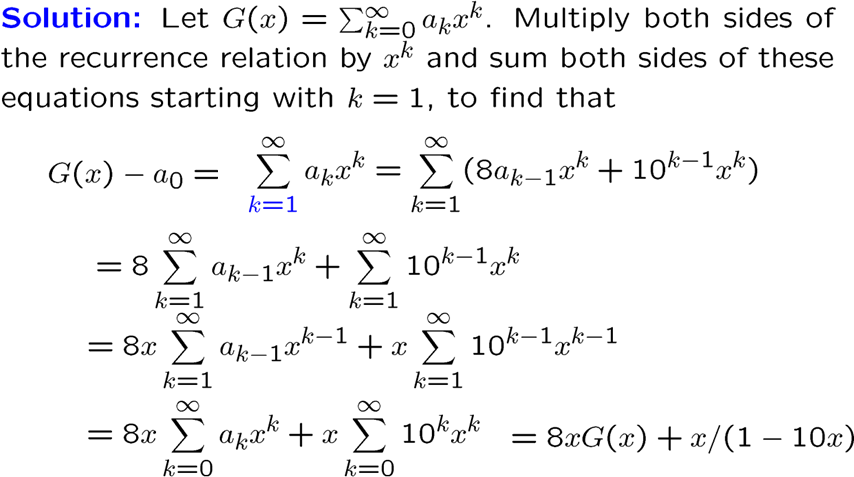
image-20240605093225728

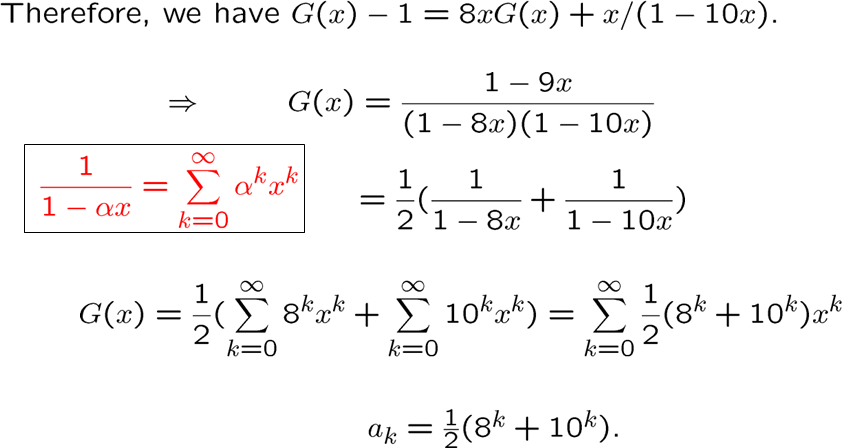
image-20240605093713265

用生成函数解计数问题

image-20240605123136663

就看这个多项式乘积里面， \(x^{17}\) 这项的系数是多少，这就是答案

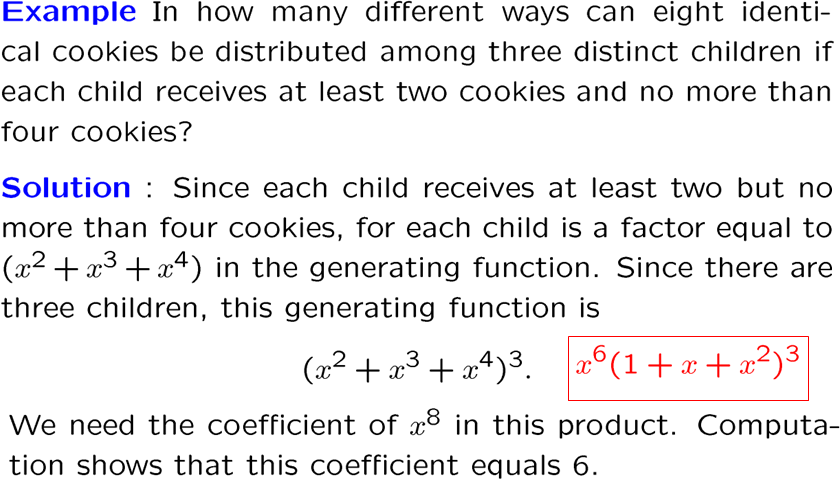
image-20240604205801789

image-20240604205906403

image-20240605123621282

r得从n开始，因为题目规定

用生成函数做排列

image-20240605124853827

image-20240605125140335

5个因子，分类讨论，分别构造生成函数

image-20240605125144881

用容错原理解决计数问题

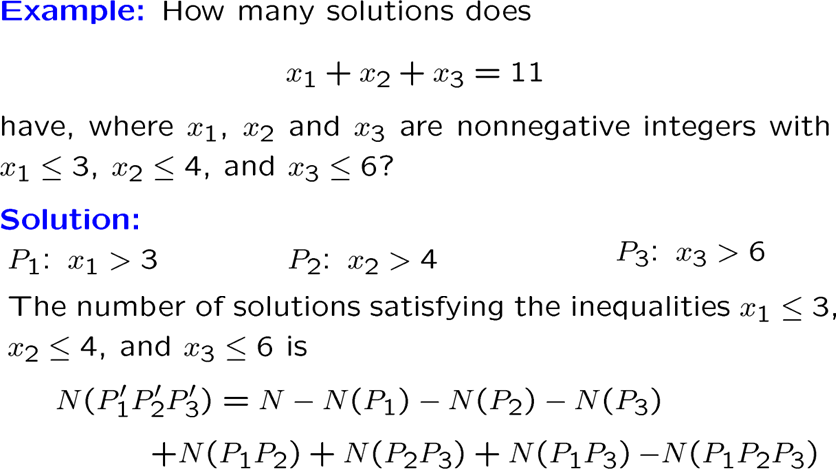
image-20240605131958920

image-20240605132511537

用容错原理解决满映射个数问题

满映射英文为 onto function

image-20240605133414956

image-20240605133027187

思路就是总的减去P1没被映到的减去P2没被映到的减去P3没被映到的

image-20240605133147819

image-20240605133357074