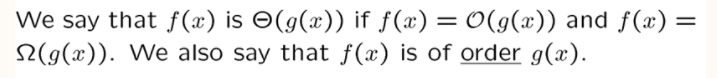Skip to content

集合与函数

:material-circle-edit-outline: 约 435 个字 :material-clock-time-two-outline: 预计阅读时间 1 分钟

集合运算

image-20240602121017011

image-20240602120304224

和命题代数几乎一模一样，实际上集合代数和命题代数都是布尔代数的同构

S 的 Power set 力集表示为 \(P(S)\) 或 \(2^S\)，包含所有 \(S\) 的子集，类似函数依赖的闭包概念

二元的 tuple 叫序偶 ordered pairs

image-20240602122255042

有限集与无限集的基数

cardinality 基数，集合元素个数

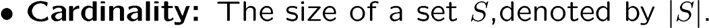
image-20240602124149547

容错原理：

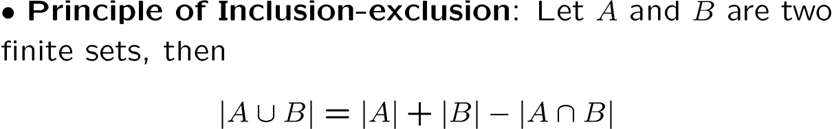
image-20240602124226264

两个集合有相同的基数，当且仅当两者之间能建立一一对应的序列

这两个集合也叫等价关系

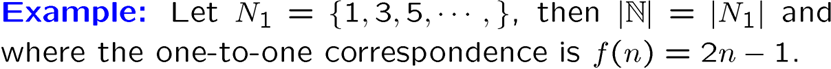
image-20240602124547159

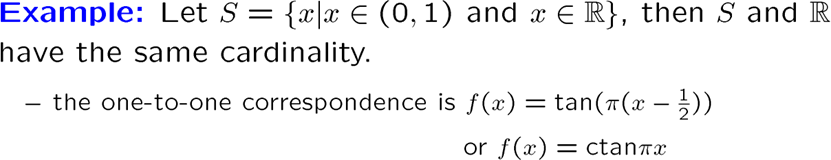
image-20240602124629838

可以看到，有限集是找不到一个真子集与其全集（proper set）基数相同的，而无限集可以

无限集可以分为可数的和不可数的，可数的就是和自然数集 \(\mathbb{N}\) 有相同基数的

image-20240602125925083

上面举的例子里，整数集可数，有理数集可数，前者是 {0，1，-1，2，-2，...}，后者表示为两素数之商，\(\mathbb{N} \times \mathbb{N}\) 也是可数的

可数不可数，形式上来说就是可不可以给元素下标，不可数的元素是不能设置下标的

无限集性质

  1. 可数无限集是最小的无限集，任意无限集都能找到比其更小的可数无限集
  2. 有限个可数集之并也可数
  3. 可数个可数集之并也可数

函数

函数就是一个集合到另一个集合的映射，且前者作为定义域，所有元素都要参与映射

  • 单射，即两个映射结果不会相同
  • 满射，即值域为整个集合
  • 一一对应，单射+满射

取整函数，往下取得是 floor function，往上取得是 ceiling function

image-20240602194735172

image-20240602194941844

image-20240621125925545