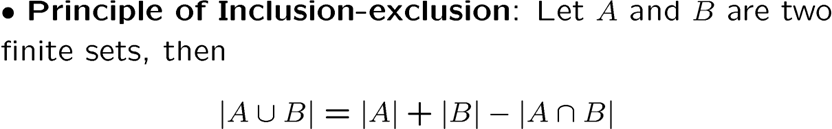递归集合与递归关系
归纳法 induction 要另外看下
递归集合
递归不止有斐波拉契函数这种递归函数,还有递归集合
递归集合定义于一个递归函数,包含初值,剩下的元素就是初值与这个递归函数生成的
例子:
一个字符串可以看成一个基于字母表集合 \(\Sigma\) 的字母序列 ,这样的字符串组成的集合叫 \(\Sigma ^*\)
两个字符串连接的操作叫 concatenation ,表示为 \(xy\)
我们可以通过递归的方式定义 \(\Sigma ^*\),先设初始值 \(\lambda\) 为空字符串,递归函数就是:
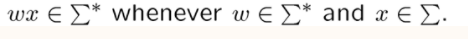
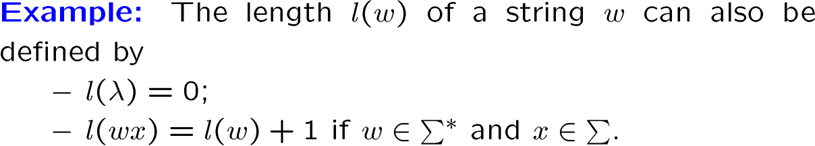
Recurrence relation
一个递归关系基于一个序列,表示这个序列的的任意 term 均可由前面的元素推出来,除了源头
递归关系的 solution 是满足这个递归关系的序列
递归的初值叫 initial condition
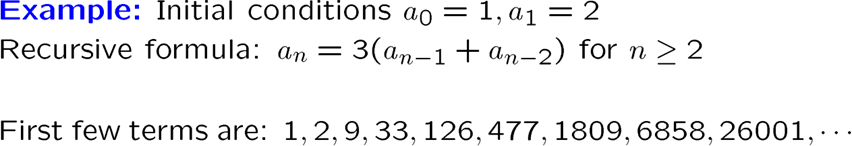
汉诺塔问题
我们需要将最底部的盘子移动到右边最底部,所以肯定得让上面的盘子都移动到中间
移动次数为 \(H_n\):

用特征方程解递归关系
常系数线性齐次递归方程

都是一次方,系数是常数,且没有常数项
这种形式的方程的解一定是 \(a_n=r^n\) 的形式,其中 \(r\) 是常数,所以我们直接将这个带入原方程,得到 特征方程(character equation),根叫特征根
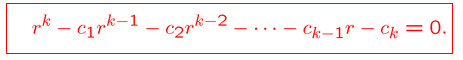
现在变成怎么解这个特征方程,我们根据指数大小来分情况讨论解法
\(k=2\) 时递归方程为 \(a_n=c_1a_{n-1}+c_2a_{n-2}\), 且特征方程只有两个解,求出特征解为 \(r_1\) 和 \(r_2\)
- 两个特征根不相等,则递归方程解一定形如 \(a_n=\alpha_1 r_1^n+\alpha_2 r_2^n\),两个 \(\alpha\) 都是常数
- 两个特征根相等,则解为 \(a_n=\alpha_1r_0^n+\alpha_2nr_0^n\),多乘了一个 \(n\)
\(k>2\)时就是有多个特征根,解法都一样
- 特征根全都不一样

- 有部分根是相同的

常系数线性非齐次递归方程
常系数线性非齐次递归方程增加了一项 \(F(n)\),不等于0,且只有 \(n\) 一个变量
每一个非齐次递归关系都有配对的齐次递归关系,叫 associated homogeneous recurrence relation,就是原递归方程去掉 \(F(n)\)
\(\{ a_n^{(p)}\}\) 是原非齐次递归关系的一个特殊解(得猜出来),这个特殊解加上配对的齐次递归关系的解,就是我们要求的通用解

如果 \(F(n)\) 满足下面这个形式,我们又可以讨论一下这时的解的形式
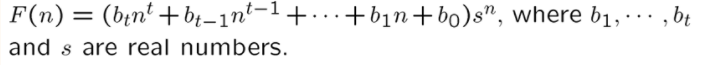
- 如果 \(s\) 不是配对方程的特征根,则解的形式如下
- 如果 \(s\) 是 \(m\) 重特征根,则解多乘个 \(n^m\)

用生成函数解递归关系
每个序列都能生成函数,可以用下面的 formal power series 进行生成

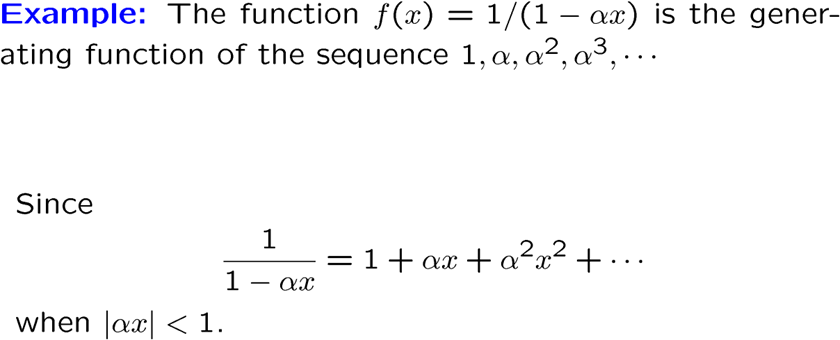
下面是生成函数的性质
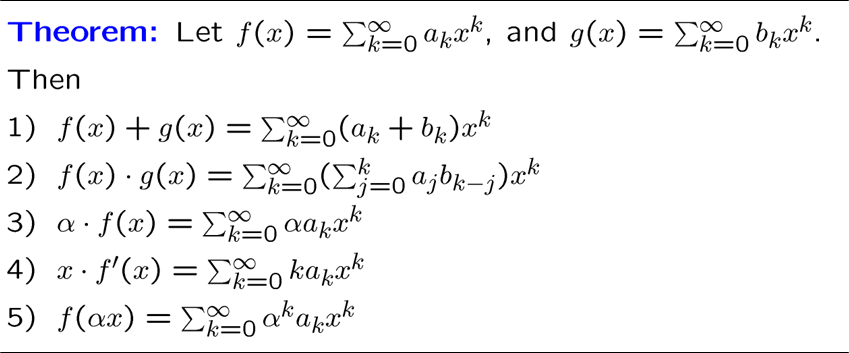
用生成函数解递归方程
做题就够了
用生成函数解计数问题
先看看 \(\{C(n,k)\}\) 的生成函数
二项式展开可以看成是 \(n\) 个 \((1+x)\) 相乘,我们可以将每个 \((1+x)\) 都看成一个因子,要么取 \(1\),要么取 \(x\),可以用来解决 \(n\) 个东西中取 \(m\) 个 \(x\) 的组合数量
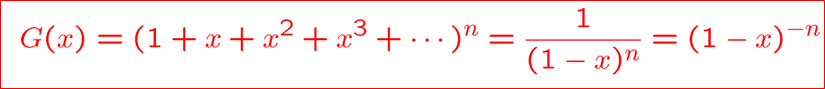

用生成函数做排列
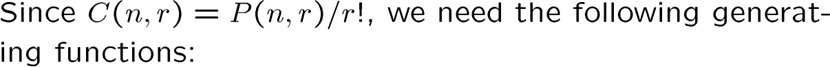

广义二项式形式的生成函数
广义二项式系数

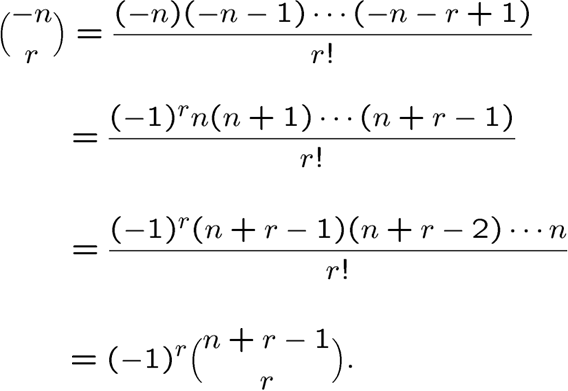
\(u>0\) 时我们得到的就是多项式展开表达式,实际上是一个泰勒展开
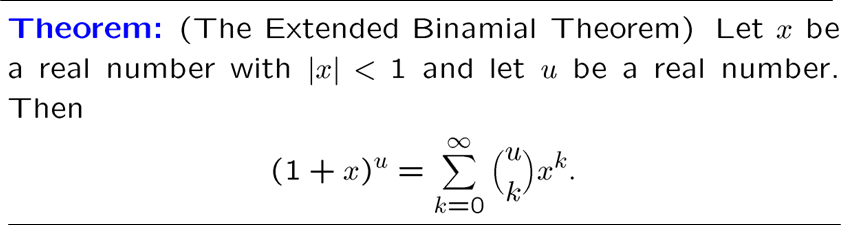
\(u<0\) 时,我们可以得到两个新的等式
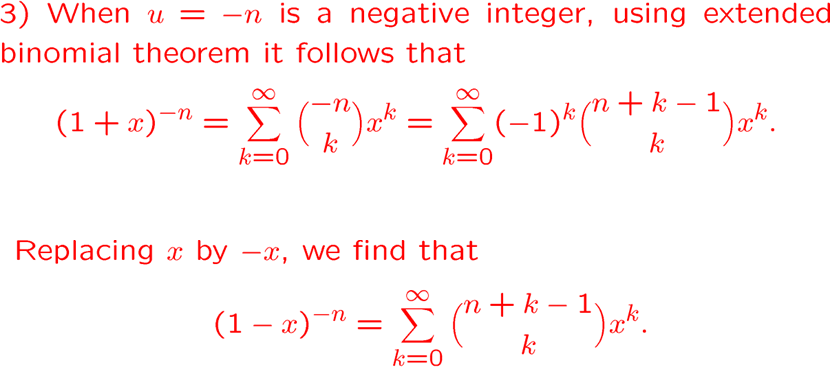
生成函数表

容错原理