Skip to content

关系

:material-circle-edit-outline: 约 1717 个字 :material-clock-time-two-outline: 预计阅读时间 6 分钟

关系定义

关系是两集合笛卡尔积的子集，包含的是某些满足特定要求的序偶

常见的特殊关系有：

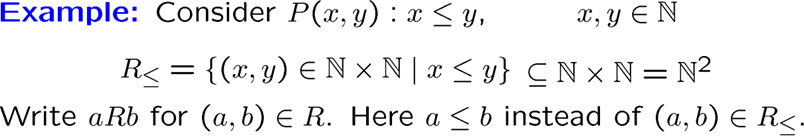
image-20240605133942449

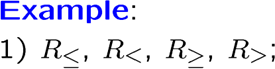
image-20240605135941169

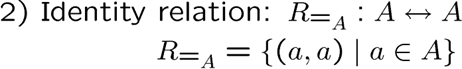
image-20240605135829048

image-20240605135954732

关系的定义域和值域

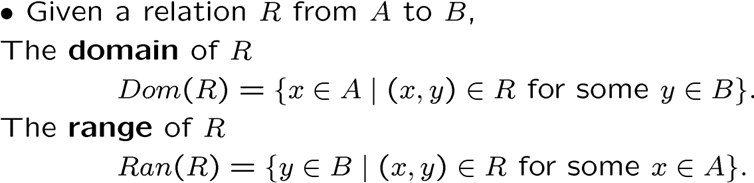
image-20240605140503858

函数是关系，关系不一定是关系，前者要求整个集合作为定义域

关系运算

二元关系其实就是带结构的序偶集合，所以集合运算规则可以用于关系，比如交并补差

有一个新的运算叫合成（composite），用了传递性，通过合成，我们可以得到乘幂关系

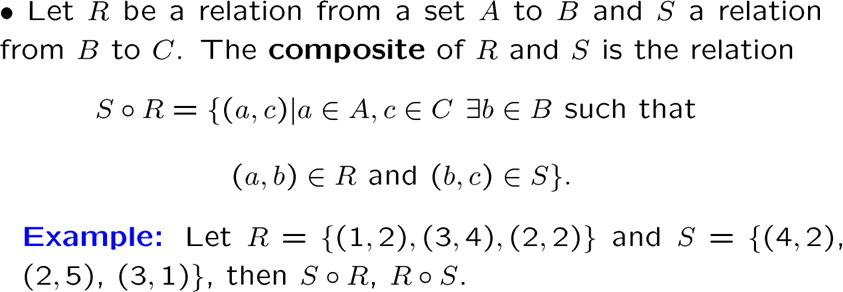
image-20240605141505821

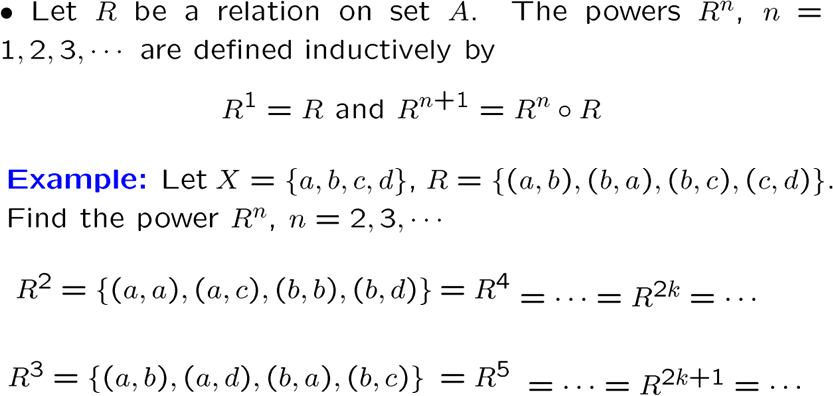
image-20240605141431449

逆关系：

image-20240605141638161

关系性质

自反与反自

自反性质，就是任意输入存在与输入一致的输出

反自性质，就是任意输入不存在与输入一致的输出

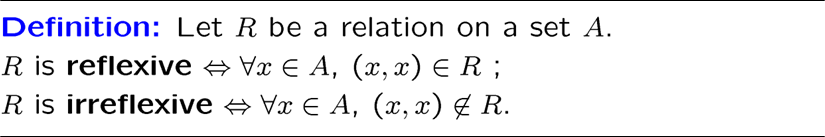
image-20240605141817277

注意不自反不等于反自

对称与反对称

反对称即只有对角线上的序偶是对称的，故恒等关系既对称又非对称

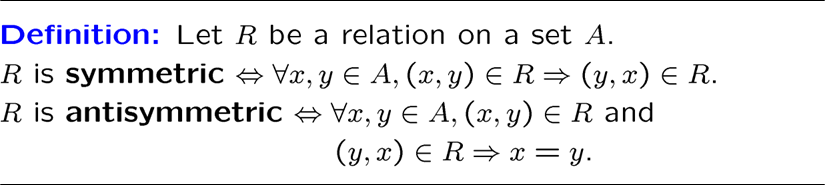
image-20240605143249338

传递性

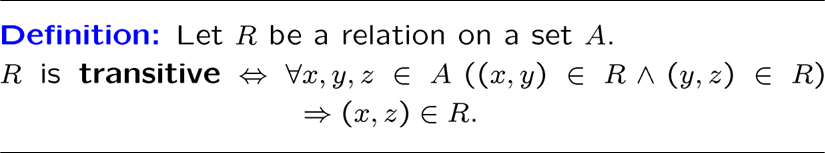
image-20240605145009150

image-20240605145005682

关系表达

关系矩阵

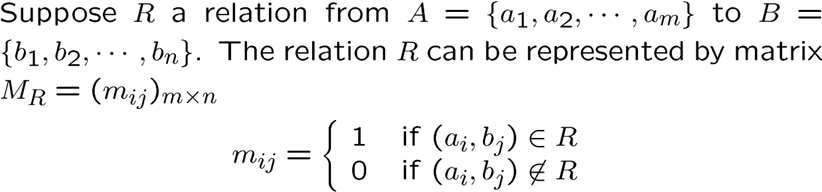
image-20240605150204274

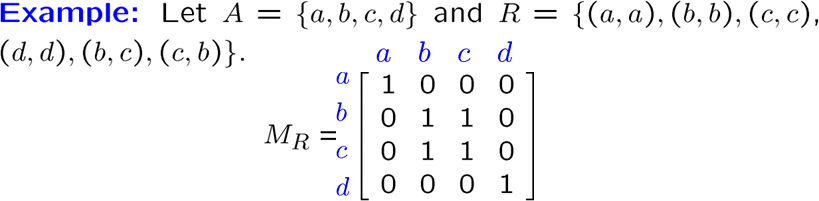
image-20240605150220910

起点对应行，终点对应列

关系性质在关系矩阵中的表现

  1. 自反 等价于 关系矩阵 main diagonal 主对角线上元素全为1
  2. 对称 等价于 关系矩阵 为对称矩阵
  3. 传递 等价于 \(M_R\) 非0位置 \(M_R^2\) 也非0

关系运算在关系矩阵中的表现

image-20240605150744038

有向图

digraph 有向图，集合里的每个元素表示为一个结点，结点之间有关系就加一个有向边

有向边表示为 \((a,b)\) ，就是序偶，\(a\) 叫 initial vertex，\(b\) 叫 terminal vertex，形如 \((a,a)\) 的有向边叫环 loop

自反则每个结点都有环，对称则有向边是一对一对的

关系闭包

闭包就是一个关系在某个性质上最小的完整拓展

image-20240605152317731

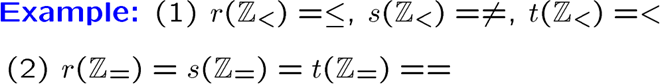
image-20240605152631242

上面的 \(r\) 表示基于自反的闭包，\(s\) 是对称，\(t\) 是传递

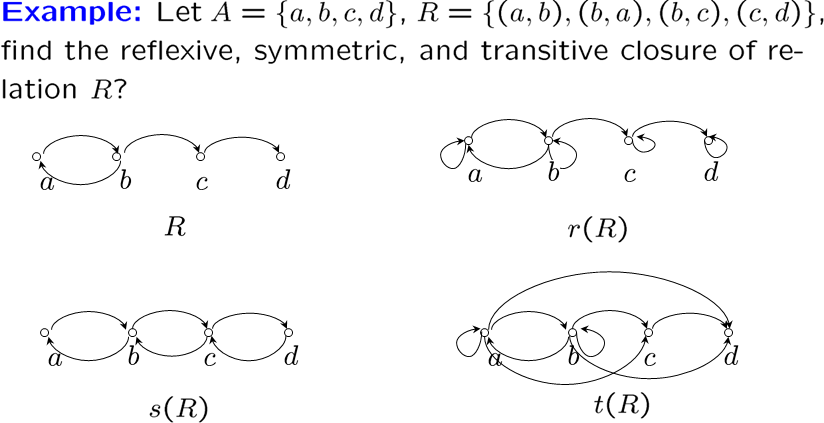
image-20240605154558654

计算闭包

image-20240605154936178

有空看看证明，PPT 有

传递闭包

  1. \(R\) 的有向图 存在长度为 \(n\) 的从a到b的道路 iff \((a,b)\) 属于 \(R\) 的 \(n\) 次合成

  2. 连通性关系 \(R^*\)囊括 \(R\) 所有可组成道路的序偶

  3. 传递闭包 \(t(R) = R^*\)

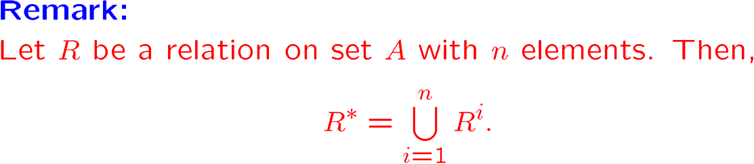
image-20240605160733917

得到传递闭包计算方式：

image-20240605161353716

\(n^4\) 的时间复杂度

我们的连通性关系是所有 有道路的序偶 的集合，这些序偶拥有长度不超过 \(n\) 的道路，这算法就是长度从1到n遍历所有道路

n次关系矩阵里面有1的序偶存在长度为n的道路

⊙是一个逻辑运算符，表示同或运算，即两个输入变量值相同时F=1，可以理解为 两个矩阵相同位置的元素相乘

Warshall's Algorithm

这算法就是fds的 Floyd-Warshall 算法，有向图求所有通道

关注道路里的内部节点，记为 \(v_1,v_2,v_3,...\) ，为了方便我们一般按矩阵从左到右的顺序

思路就是，先找出所有道路的内部节点只有 \(v_1\) 的序偶，然后允许加入 \(v_2\)，以此类推，一步步放宽

image-20240606092839350

对于一对序偶，如果其存在只包含前 \(k\) 个结点作为内部节点的道路，那么只可能属于两种情况

  • 要么其存在只包含前 \(k-1\) 个结点作为内部节点的道路
  • 要么 \(v_k\) 正好能连通两者

image-20240606141851202

无脑计算步骤

  1. 先找到该矩阵的对角线，并从对角线的左上方开始为第一个元素

  2. 以对角线上第一个元素为中心，按列展开，寻找中心所在的列中所有不为0的元素

  3. 将“ 该中心所在的行 ”加到“ 该中心所在的列 ”中所有不为0的元素所在的行上

  4. 加完之后，以对角线上第二个元素为中心，按列展开，寻找该列中所有不为0的元素

  5. 重复“ 操作3 ”

  6. 一直到将对角线上所有元素都展开后结束。

还是看例题更容易理解：

image-20240606095511501

\(W_0\) 就是 \(M_R\)

image-20240606095820764

元素分类

等价关系 equivalence relation

等价关系 \(R_\sim\) 是一种特殊的关系，要求自己映射自己，且自反对称传递都满足

比如同姓关系，人映射到人，同一个姓的两人组成一个序偶

等价类 equivalence class

比如同姓关系，你姓张，那你的等价类就是所有姓张的人，展开说就是所有与你有组成序偶的元素组成的集合就是你的等价类，表示为 \([你]_{R}\)

image-20240606143819088

等价类的有向图任意一对结点都有来回的通道

性质：

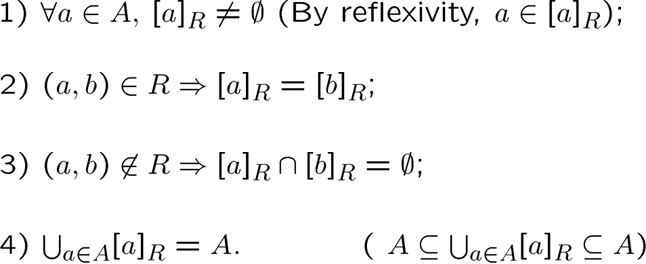
image-20240606144009074

第四条意思是所有的等价类并在一起就是整个集合

所有等价类组成的集合实际上是集合与关系的商

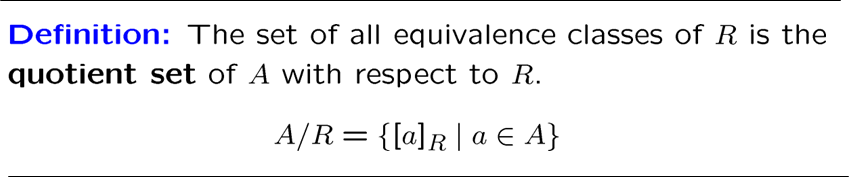
image-20240606144207523

划分 partition

一组互不相交的集合的并能组成另一个集合，那这组集合就是该集合的一个划分

一个关系的所有等价类组成了一个关于集合的划分，相对的，对于一个集合的任意划分，我们都能将其视为等价类找到对应的等价关系

偏序（部分次序）

给集合内部进行了分类，接下来尝试给集合内部排序

偏序是一种特殊的关系，自己和自己组合，且满足自反、非对称、传递，相应的集合叫偏序集 partial order set / poset

image-20240606155316501

元素 \(a\) 和 \(b\) 之间是能比出谁大谁小的，就叫 comparable，否则就 incomparable

一个偏序集所有元素都可比较，则叫 全序集/线序集/链集 totally order/linearly order/chain

字典序就是一种完全序

image-20240606160828711

哈斯图 hasse diagram

我们可以画 hasse diagram 来表现偏序里的次序，画法如下

  1. 画出偏序的有向图（不要忘了偏序是一个关系）
  2. 去掉所有的环
  3. 去掉所有由传递性得到的边
  4. 起点放下方，终点放上方，边去掉箭头

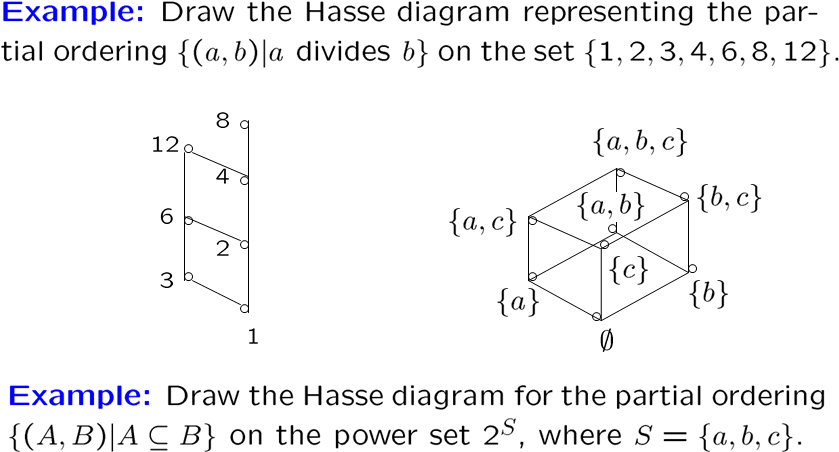
image-20240606161317833

偏序的极与最

集合内找不到更大的是极大，比集合内任意元素都大是最大

问题就在偏序里面可能存在不能比较的元素，有不能比的就不会有最大的

  • 极大是 maximal，极小是 minimal
  • 最大是 greatest，最小是 least element

上界可以不是 \(B\) 里的元素，只要大于等于 \(B\) 里所有元素即可，上确界就是最小的上界

  • 上界是 upper bound，下界是 lower bound
  • 上确界是 greatest upper bound，下确界是 least lower bound

image-20240606162112142

良序 well-ordered

任意非空子集都有完全序上，且都有最小元，那这个集合就是一个 well-ordered 集

格 lattice

一个 lattice 就是偏序集里的一对元素，且这对元素需既有上确界也有下确界