Skip to content

树

:material-circle-edit-outline: 约 520 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟
  • 树：无简单回路的连通无向图叫树，任意两个结点均存在唯一简单道路的无向图也叫树
  • 森林：无简单回路的无向图叫森林
  • 根树：指定某个结点为根，由此边可以有方向了，这样的树叫根树 rooted tree，由此有了儿子，兄弟，祖父，子孙、父亲、叶子、内部、子树等概念
  • 层数：结点的 level 即根到结点的简单道路长度，即层数，树的 height 即最大的 level
  • m 叉：(full) m-ary tree，即 m 叉树，full 就是儿子满了
  • ordered rooted tree，即每个内部结点的儿子有顺序，可以分为左儿子、右儿子，左子树、右子树
  • 满足AVL树要求的树就是 balanced 的

一些性质：

  1. 树的顶点比边多1个，即 root
  2. 含有 i 个内部结点的满 m 叉树的顶点数为 n=mi+1，多一个是 root
  3. 对于 m 叉满树，\(n\) 个节点有 \((n-1)/m\) 内部节点（列方程 \(n=mi+1\) 和 \(n=l+i\)）

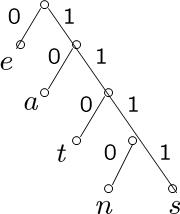
前缀码

prefix code，任意编码都不会成为其它编码的前缀，避免一长串二进制数能解码出不同的字母组合

例如，0，10，110，1110，1111

前缀码可用哈夫曼树表示并优化，使用频率越高的字母放在越上面即可优化

image-20240619104318017

生成树

简单图是连通的当且仅当其有生成树

可以用DFS构造生产树，DFS也叫backtracking

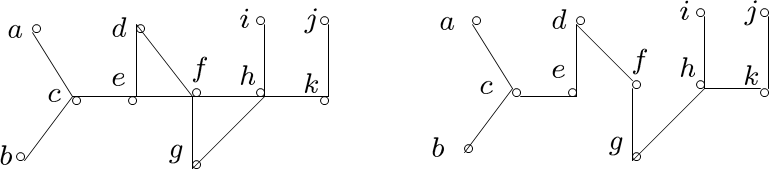
image-20240619114001847

也可以用BFS

image-20240619124621505

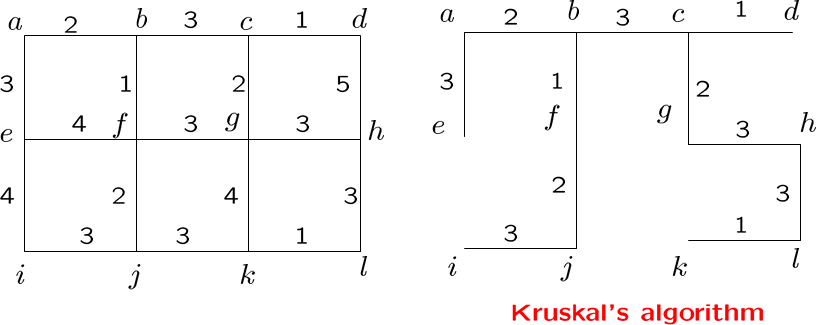
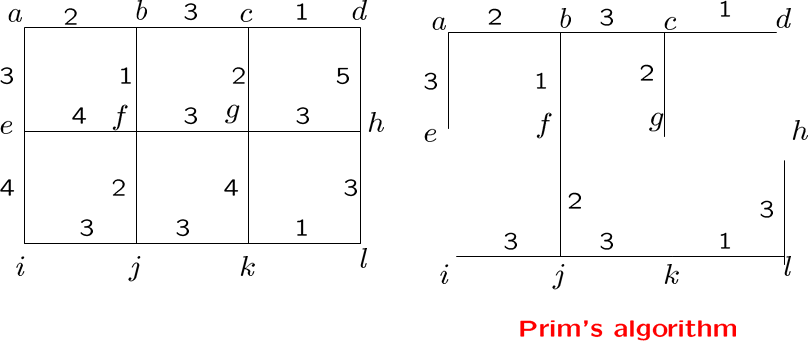
最小生成树

最小生成树是指边权重和最小的生成树

用Kruskal或Prim算法，他们都是贪心算法，即每一步决策都只选最优的策略

Kruskal算法每轮选所有边中权重最小的边加入解集，检测有无回路生成，有则撤回，不再考虑这条边，加到 n-1 条边位为止

Prim算法则是先选最小的边，每轮从相邻边中选最小的加入解集，检测有无回路生成，有则撤回，不再考虑这条边，加到 n-1 条边位为止

image-20240619144951855

image-20240619144956696