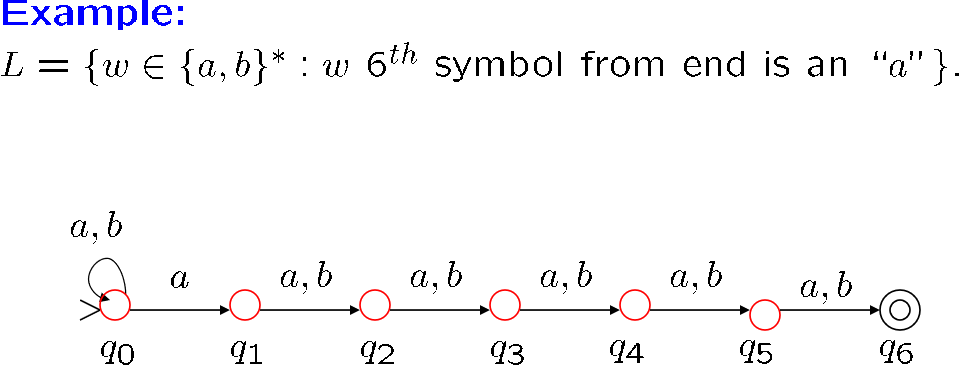Skip to content

Chapter 2 Finite Automata

:material-circle-edit-outline: 约 482 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

Deterministic Finite Automata(DFA)

确定性有限状态机，确定性是指每一步的状态转移是确定的，有限是指状态是有限的

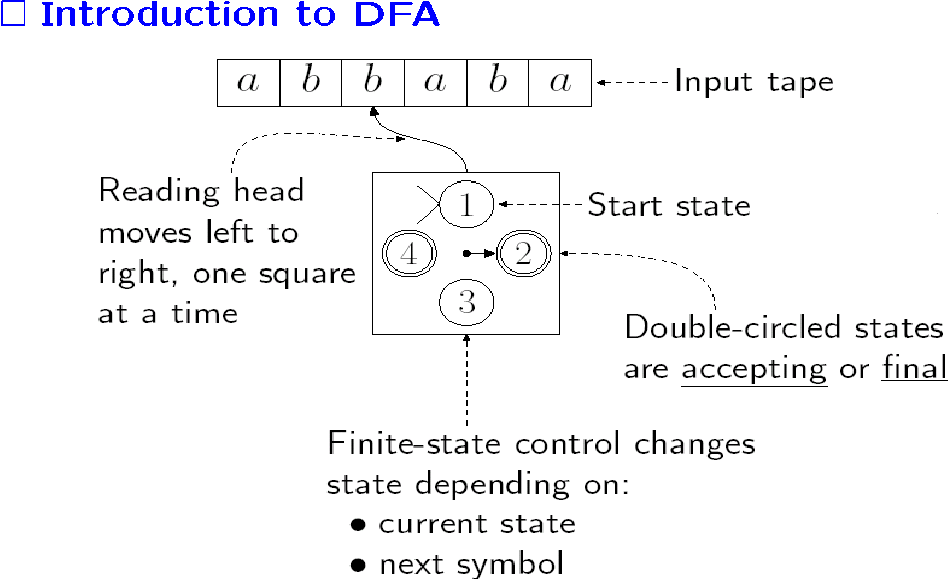
image-20240929183921269

有一个输入带，只能读，读取头只能向右移，每次只读一格，读到一个字符就改变状态

image-20241007095843279

转移方程在图里就是一条边

image-20241007100052810

image-20241007100210638

没星号是一步，有星号是有限步

e是空字符，一个字符串能被DFA接受/判定，当且仅当该DFA存在末状态能让该字符串被完全消耗掉

具体而言，就是带入一串字符串，通过传递函数后结果状态是末状态

image-20241007100834713

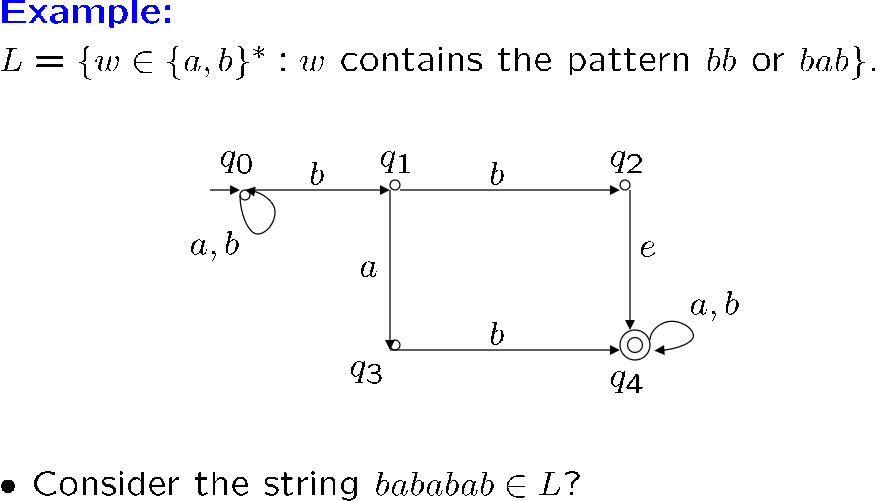
用图来表示状态转移

死去的数逻开始攻击我

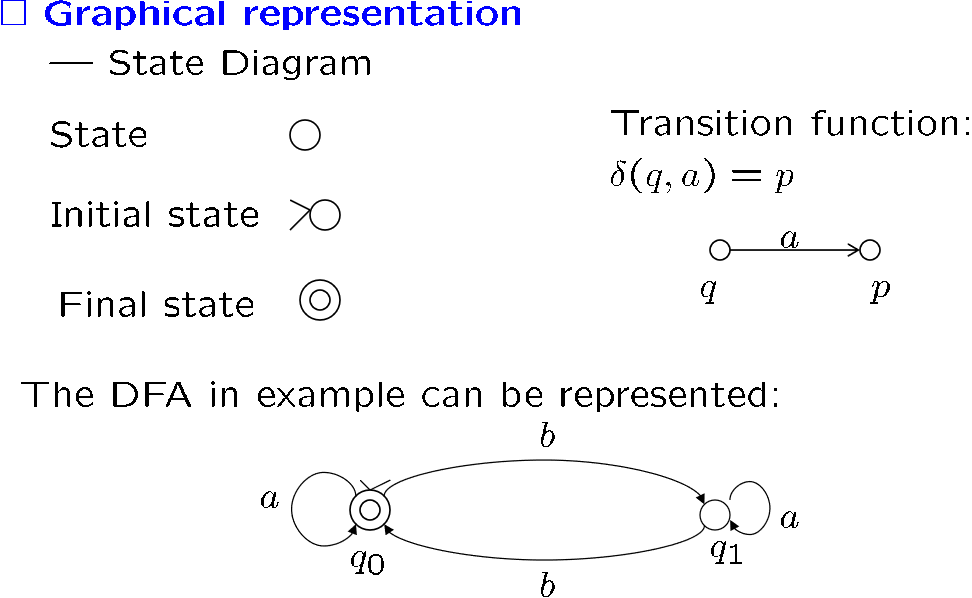
image-20241007101235073

image-20241007101656965

这个例题再看看

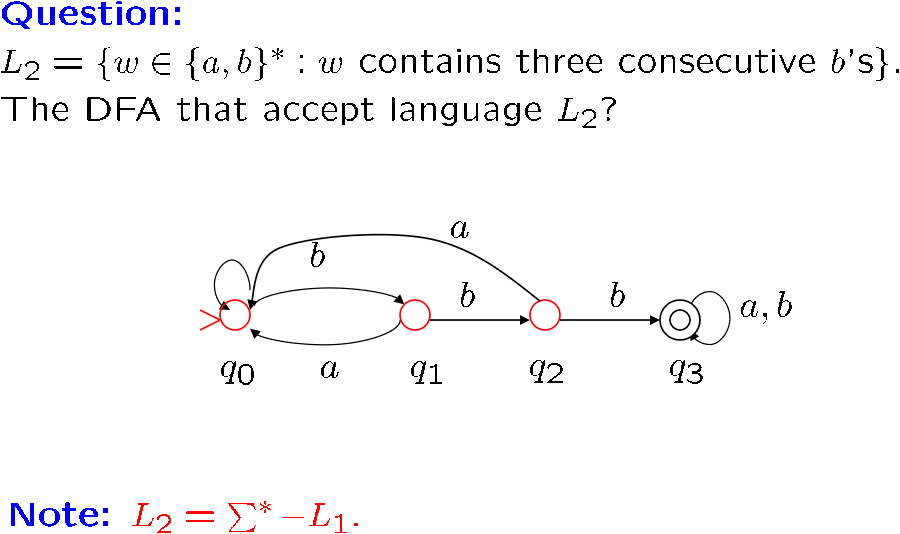
image-20241007101909510

这种方法只适用于DFA，这就是P和NP的区别

什么是确定性

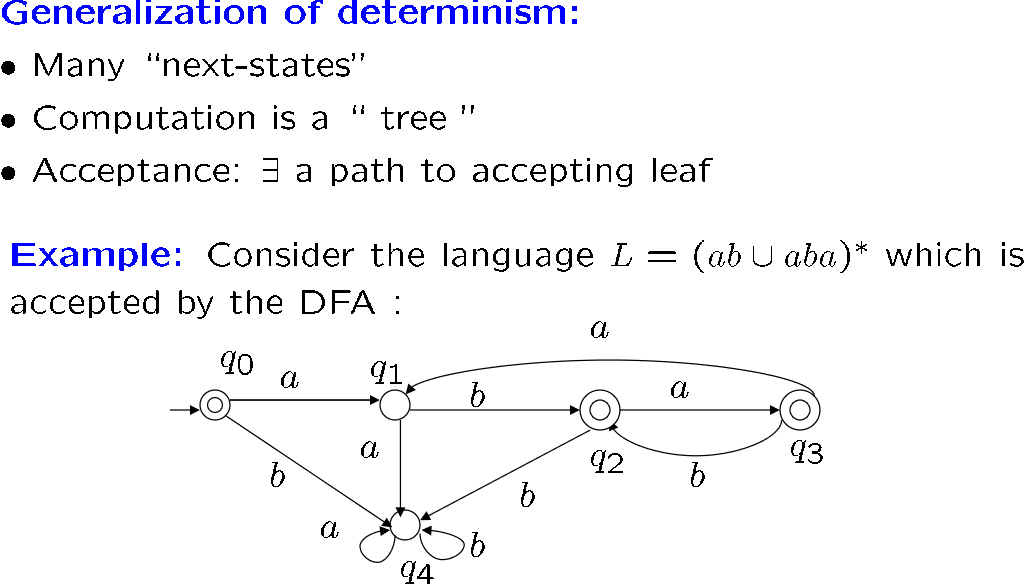
image-20241007102730130

image-20241007102758790

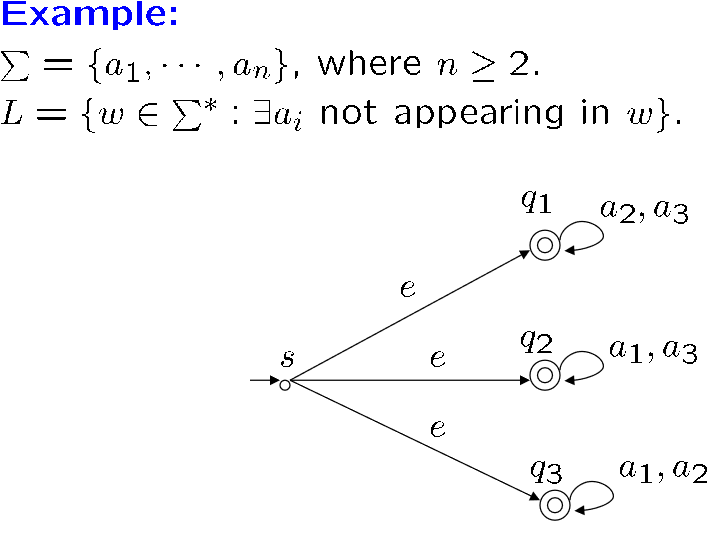
下面这个是NFA答案

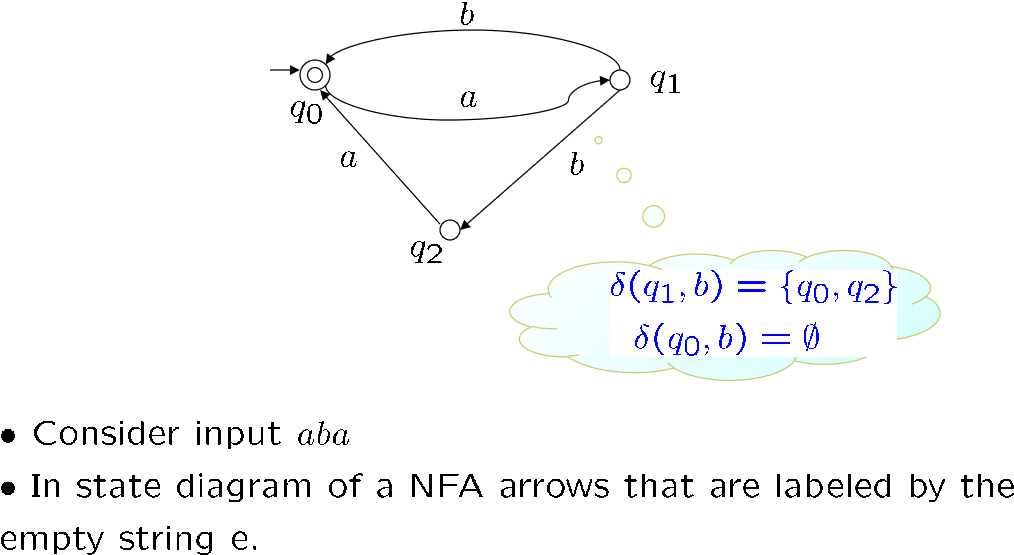
image-20241007102938652

这个问题NFA更容易设计，我们是可以先设计NFA再转化为DFA的

很明显，一个状态读到一个字符可以没有动作，可以有多个动作

Nondeterministic Finite Automata（NFA）

不确定性有限状态机，在DFA基础上希望改进性能而出现的

把传递函数从确定的改成不确定的，原本是一对一，改成一对多，可选择的

image-20241007103300470

NFA把DFA的转移函数改成转移关系了

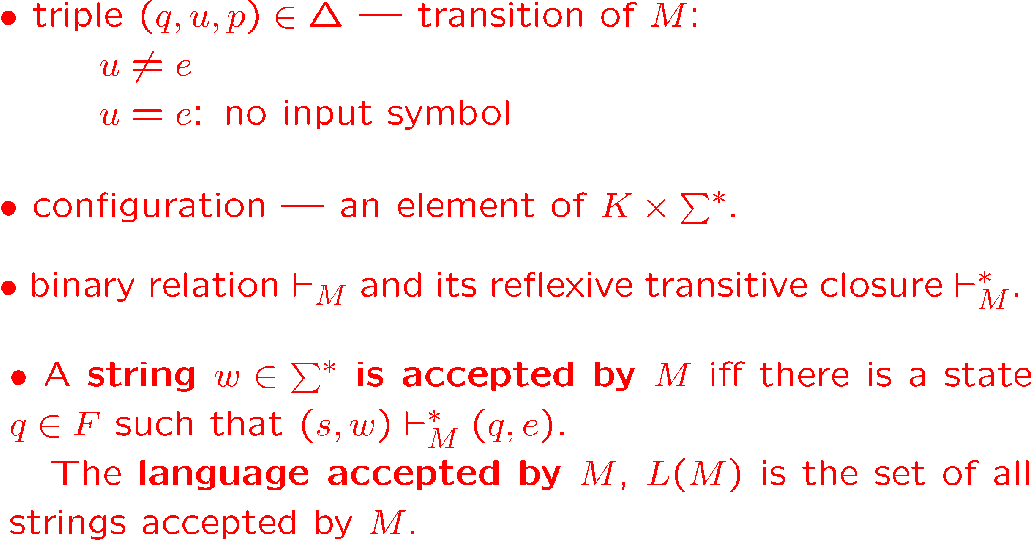
image-20241007103308214

对应一个字符串，只要存在至少一条路径能够消耗掉那就能接受

\(L(M)\) 即一个状态机能接受的所有字符串的集合

所以NFA需要深度遍历整棵树，而DFA类似BFS找一个叶子

下面有些例子可能会觉得莫名其妙，需要记住，这些状态机的作用是表征特定的字符串，即只消耗特定的字符串，所以莫名其妙的部分是用来过滤的

image-20241007103319238

image-20241007110132439

image-20241007110204663