2.2

:material-circle-edit-outline: 约 652 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

FA 与 正则表达式

regular expression

封闭性

能被 FA 接受的语言，基于下面五个运算符是封闭的

封闭性即在里面怎么运算都还是在里面的，比如整数对乘法封闭，自然数对减法不封闭

我们可以针对五种运算符构造相对应的 FA 来接受相应的语言：

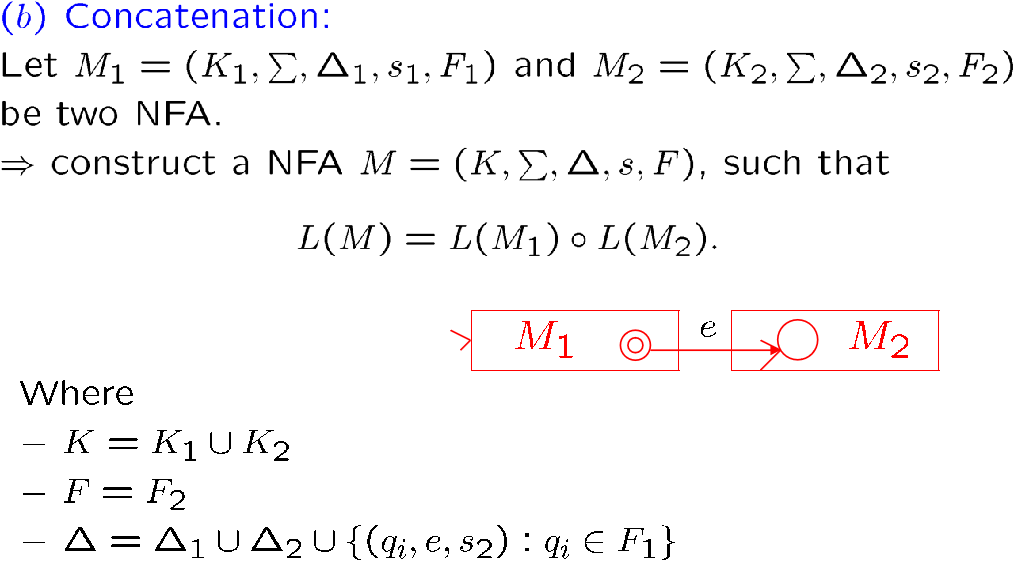
即，0~n 次连接

相当简单

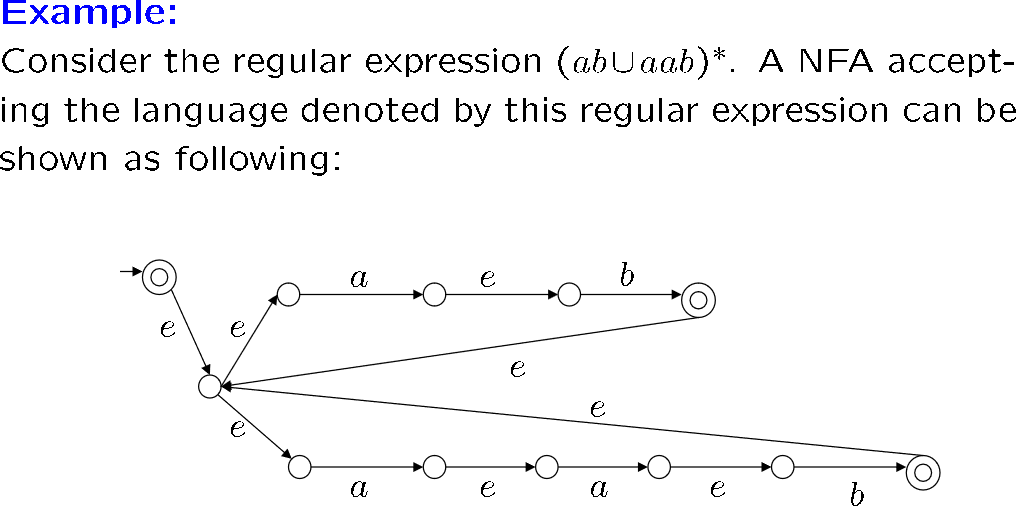
由上可见，任意正则语言都能构建一个 FA 进行吸收

实际上，FA 和正则表达式是等价的：

• 一个语言是正则的，当且仅当其可以被一个 FA 接收；即任意正则表达式均可被某个 FA 接受
• 可被 FA 接收的语言都可以被正则表达式表达

我们还需要证明第二条，即任意 FA，有 \(L(M) = L(R)\)

证明的思路是，对于任意 FA，我们构造一个正则语言 \(R\)，证明其就是该 FA 能接受的语言

\(L(M)\) 实际上就是起始状态到终点状态的所有有向道路

证明

我们定义字符串集合 \(R(i,j,k)\)，其元素能够从 \(q_i\) 走到 \(q_j\)，且经过的中间状态的最大下标为 \(k\)

显然这个 \(R\) 包含所有起始状态到终点状态的有向道路

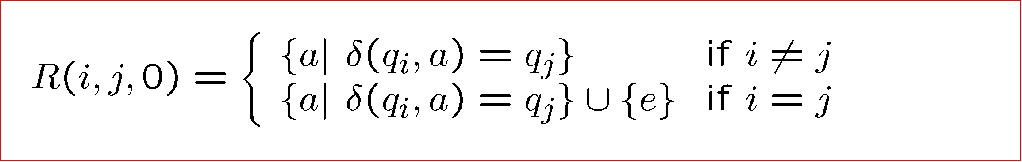
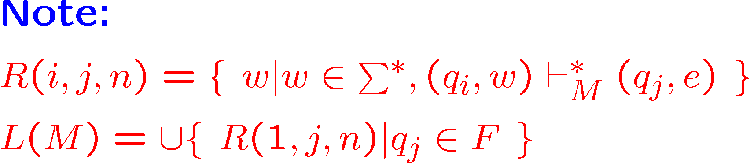
然后我们证明这个是一个正则语言

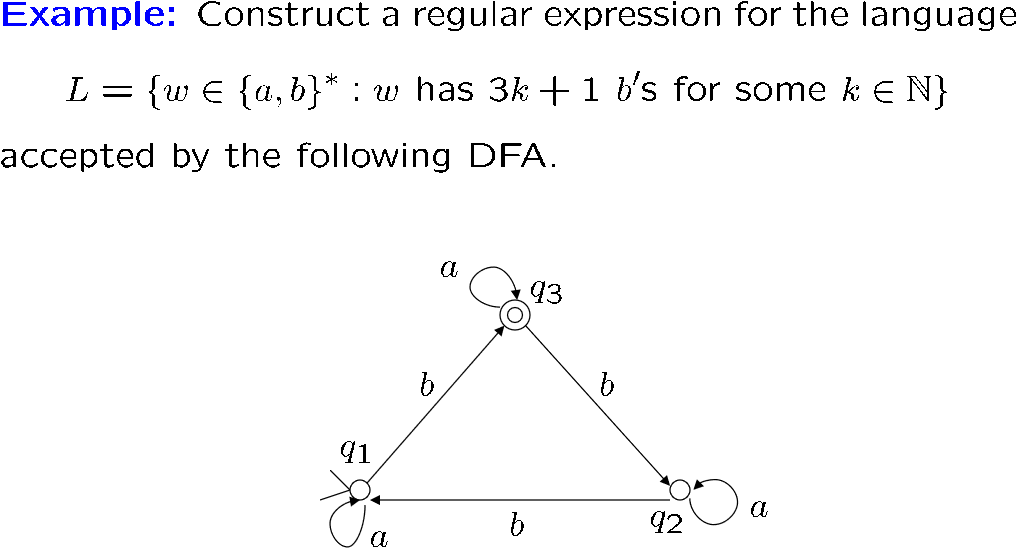
关于求一个 FA 能接受的语言，只需要一步一步求 \(R(i,j,k)\)，为了方便，我们可以每求一轮就把对应的 \(q_k\) 删掉

如果有多开头，多结尾，就分别求，例如下面先求 \(q_4\rightarrow q_5\) 能接受的语言

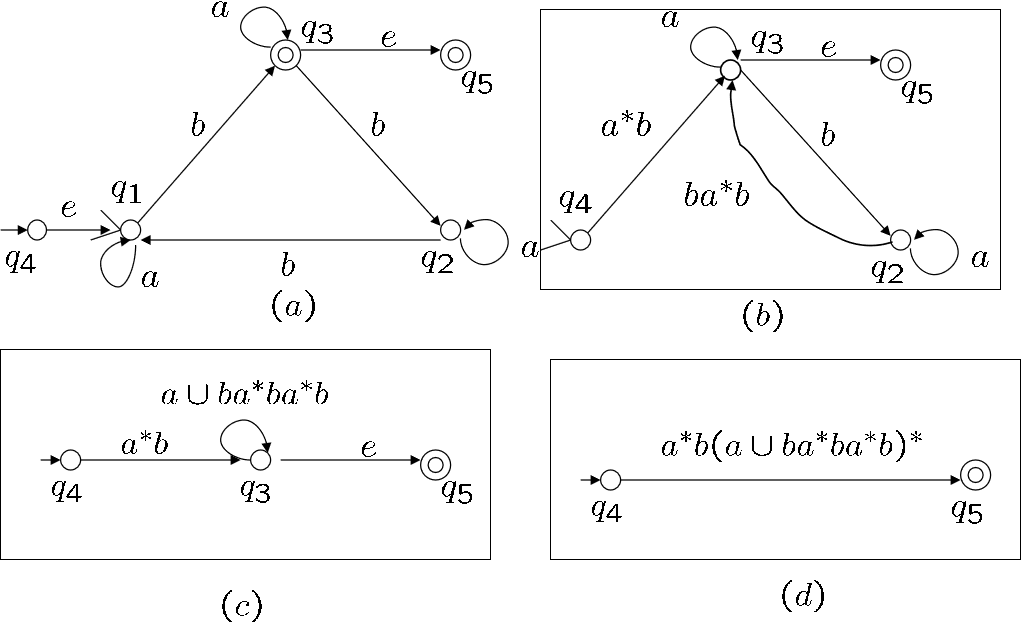
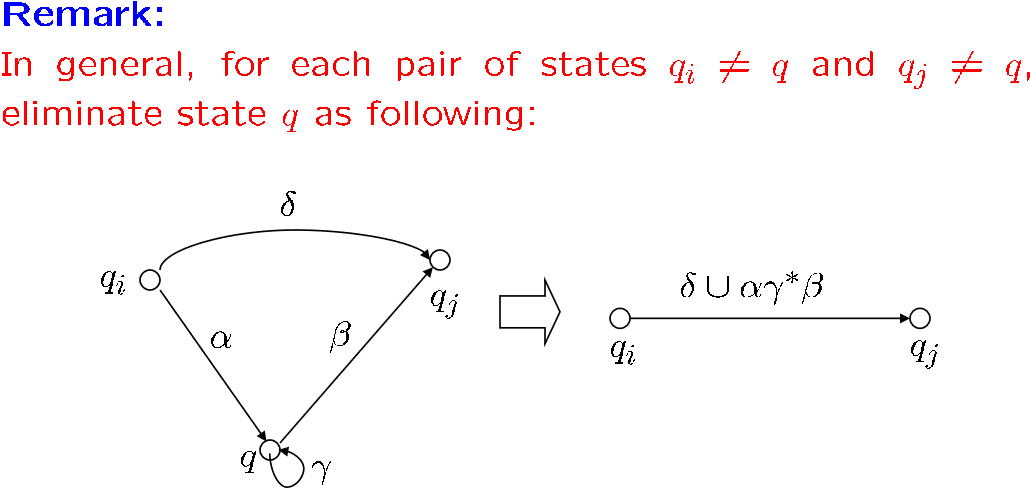
我们现在已经可以根据正则表达式写出 FA，根据 FA 得到对应的表达式了

判断一个语言是不是正则的

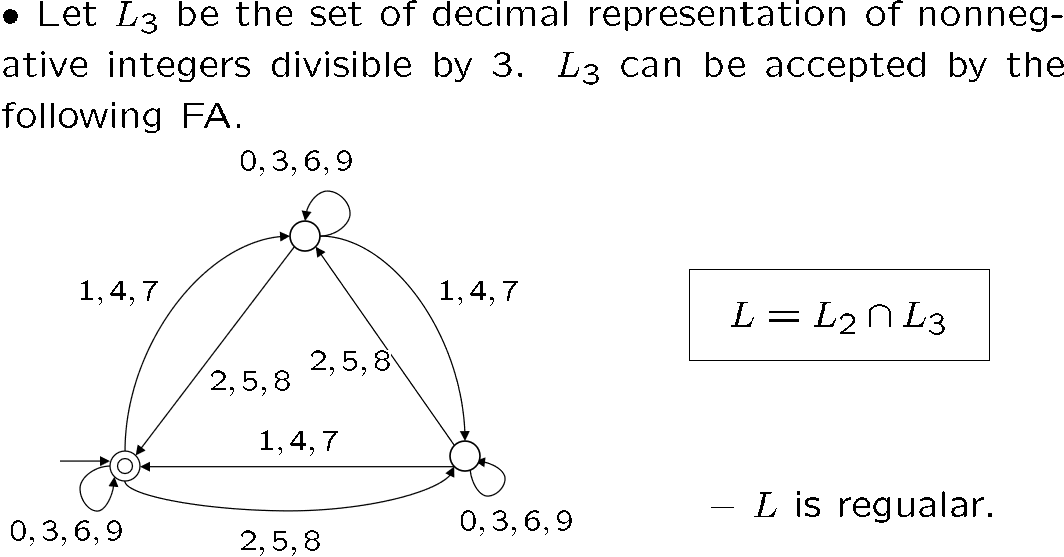
证明正则性的三个思路

• 构建正则表达式来生成这个语言（封闭性）
• 构建一个能接受其的 FA （正则与 FA 等价）
• ？？？

非正则语言

FA 是有限机，无法处理数量不确定的（无周期性的）语言，即带变量的语言，例如 \(a^nb^n,n>0\)

正则语言有以下性质

证明很简单，注意条件是 \(\omega\) 长度 \(\ge n\) ，故一定会经过 n+1 个状态，其中至少一次重复经过同一个状态，由此可以构建对应的 \(x,y,z\)

我们可以借助上面的性质证明某个语言不是正则的

证明思路如下：

还有一种办法

注意是 $\exist n,\forall \omega $