2.3 DFA State Minimization
:material-circle-edit-outline: 约 491 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟
最少状态数的 DFA State Minimization
对于某个 DFA,我们尝试找一个等价的 DFA,让其拥有最少的状态数
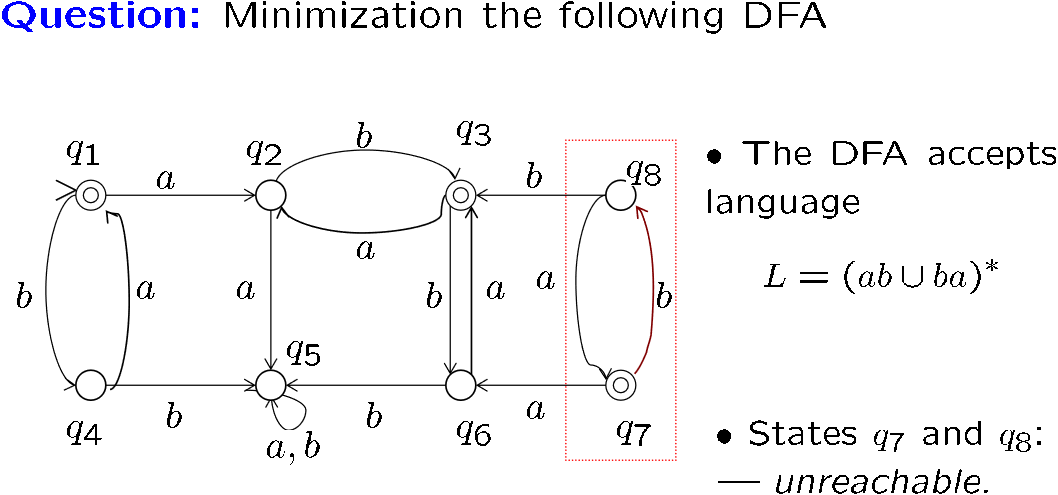
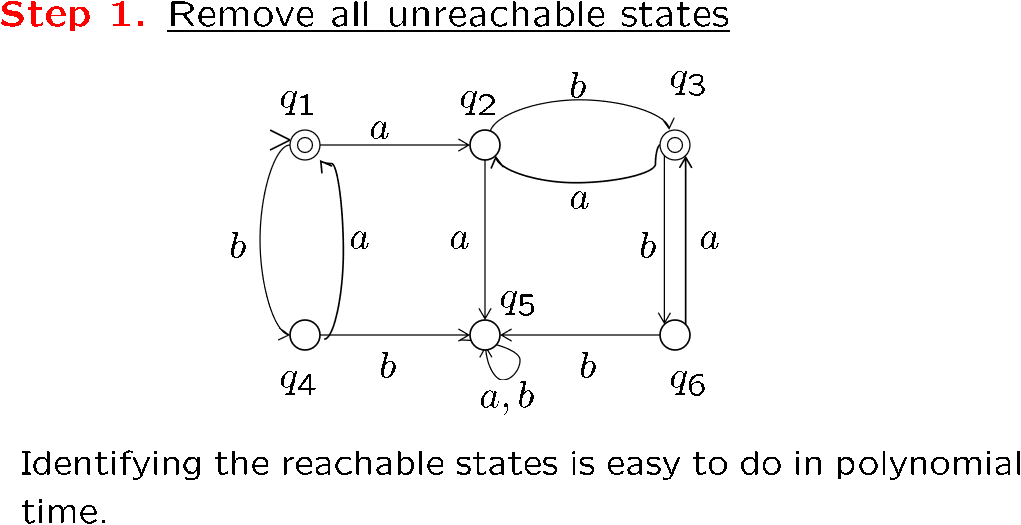
移出所有不可达状态,等价于找出所有可到达状态,后者更简单,算法如下:

再将等价的状态进行合并:

状态等价就是在这个状态上,输入相同的字符能得到同样的结果
字符串等价就是输入后能得到相同末状态
关于语言等价的等价类
等价有三个特性,自反,对称,传递,满足的话就是等价
定义语言的等价关系


这四个就是 $\Sigma ^\star $ 的一个划分
关于机器等价的等价类
输入同一个机器,最后停在相同状态,就是等价的
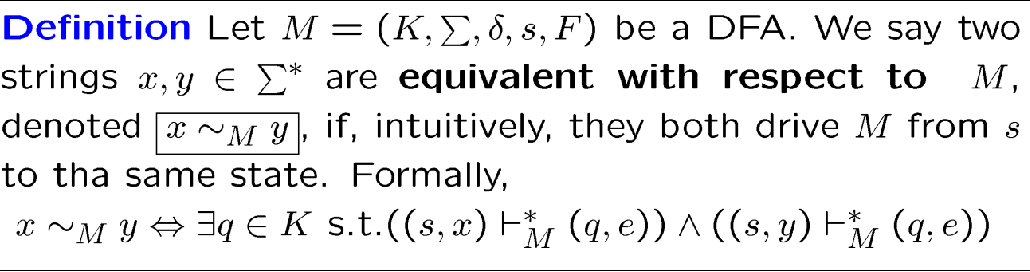
\(E_q\) 表示所有会停在 \(q\) 上的字符串
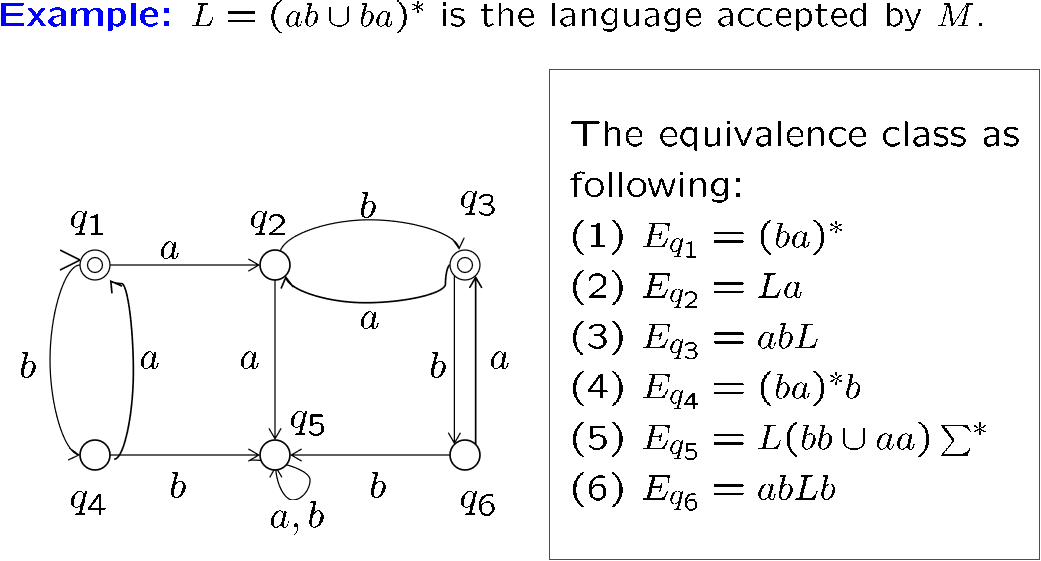
两种等价关系的关系
机器等价类更细,是在语言等价类上进一步划分的


refinement 即细分,前者划分地更细,而且是在后者的基础上进行划分的

我们想,能不能让机器等价类刚好与语言等价类一模一样,不要细分
答案是可以的,我们只要从语言等价类出发去构造 FA,保证得到的 FA 等价类不变即可
构造方式见证明:


我们还需要证明:
- K 是有限的
- \(\delta\) 是一个函数
- L = L(M)


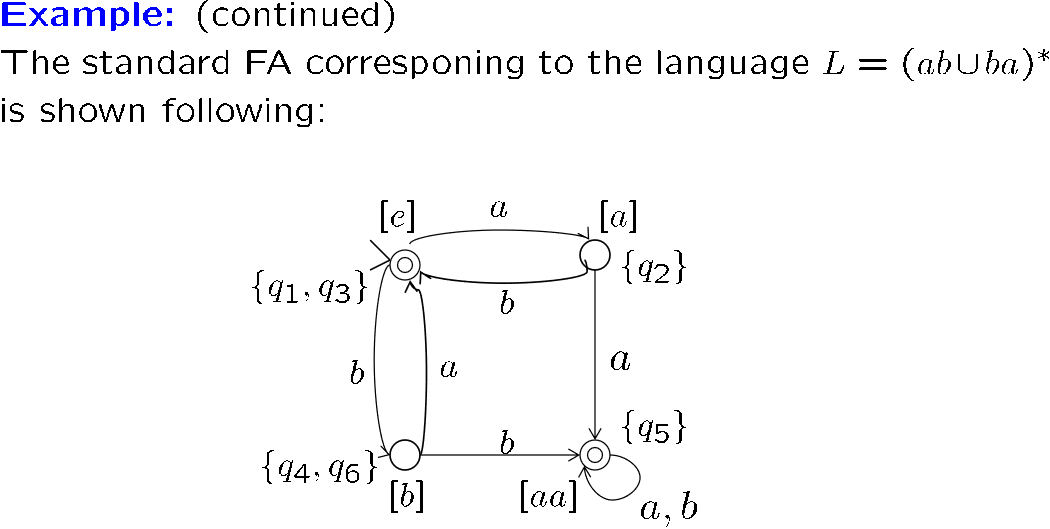
等价类与正则语言

这个定理可以用来证明某语言不是正则的
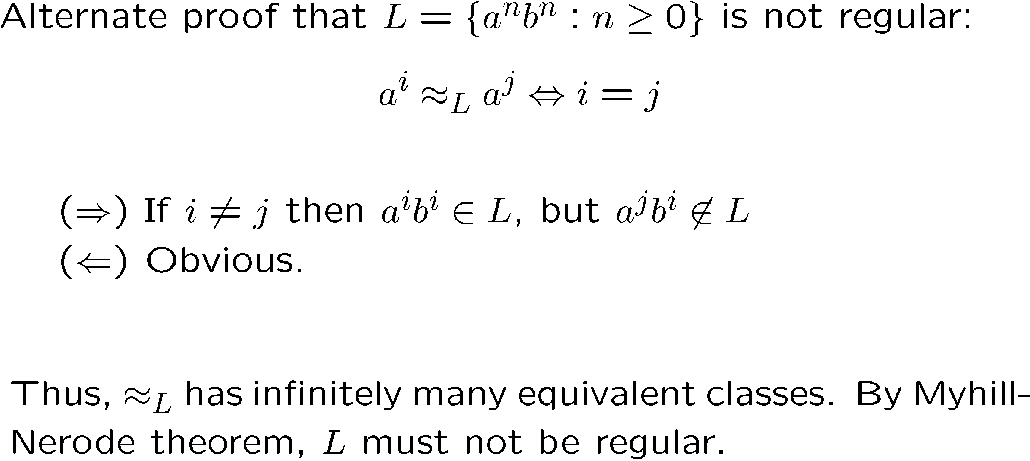
FA 最小化算法


两个状态等价的意思是,对任意字符串,要么都是能进入末状态,要么都不是
最小化算法的思路是,一步步合并等价状态
看例子吧