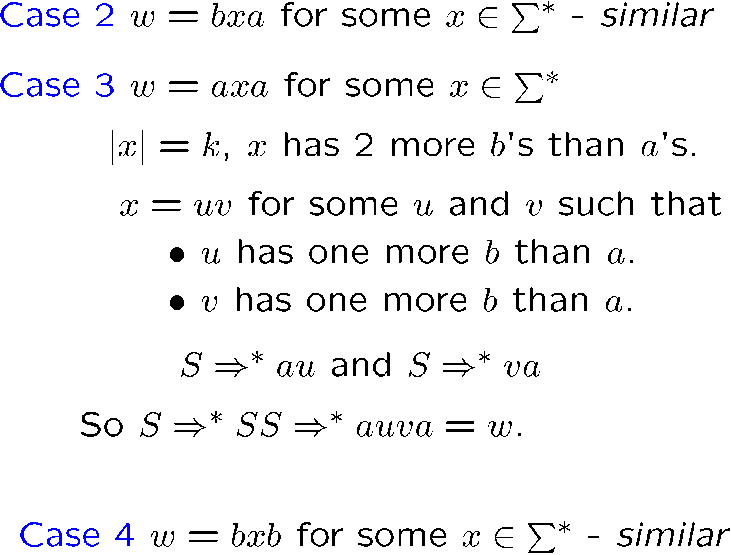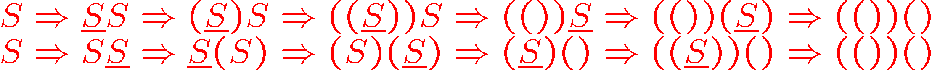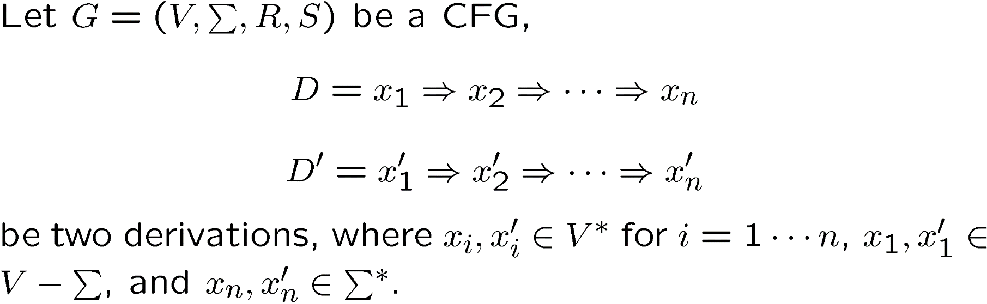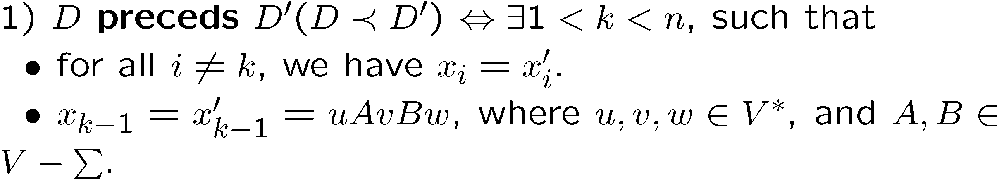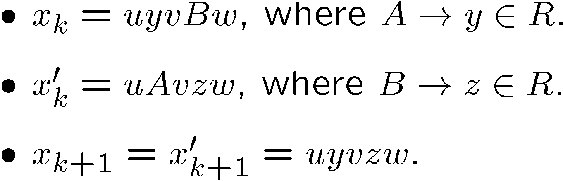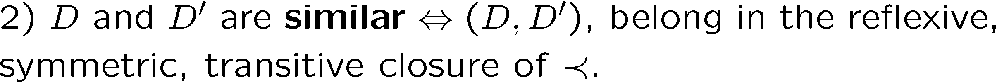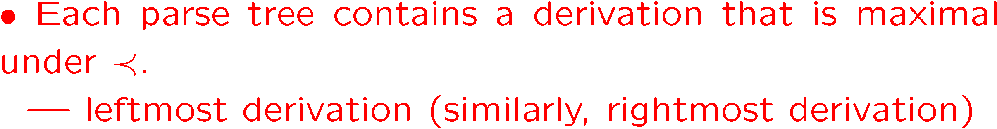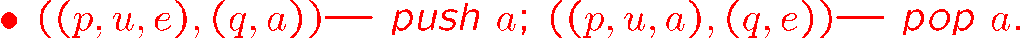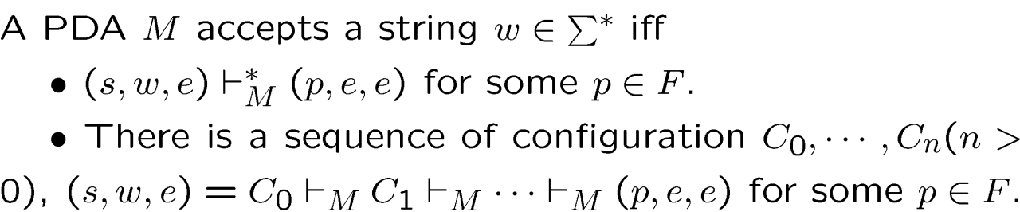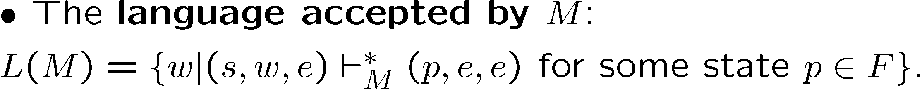Chapter3 Context-Free Language

:material-circle-edit-outline: 约 831 个字 :material-clock-time-two-outline: 预计阅读时间 3 分钟

PPT 智云课堂

我们之前学了正则语言和对应的 FA，但是还有很多语言不是正则的

Context-Free Language 是一个更强大的语言

什么是上下文有关

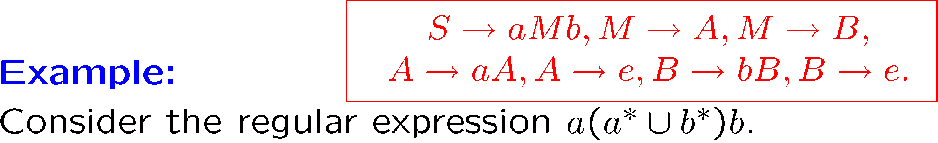
上面红框里的是可以生成这个正则语言的文法，这里的文法没有上下文约束

形如 aB->aBc 的就是有上下文约束的，B 展开的前提是前面有个 a

CFG 定义

我们学的是上下文无关语法

\(L(G)\) 是能通过 \(G\) 生成的所有语言的集合

\(L\) 是一个 context-free language（CFL），当且仅当 \(\exist\) 一个 CFG \(G\)，\(L=L(G)\)

[!EXAMPLE]

还有另一种证明方法

而且，所有正则语言都是 CFL

[!NOTE] 所有正则语言都是 CFL

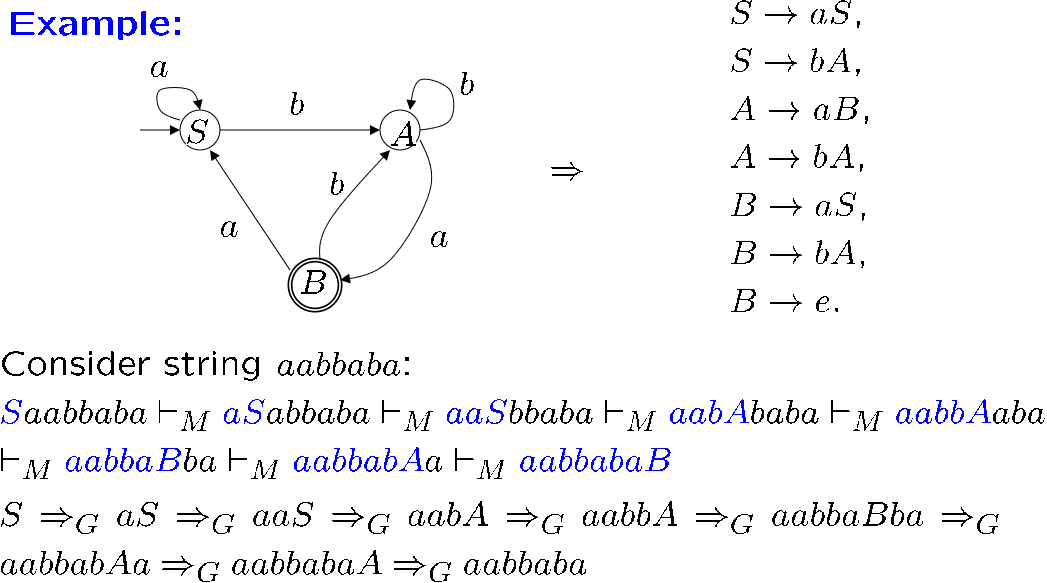
我们将直接从正则语言构造出对应的 CFG 来证明这事

假设一个正则语言对应的 DFA 为 \(M=(K,\Sigma,\delta,s,F)\)

可见只需要把每条边进行一定的描述，就得到了对应的上下文无关文法，如何转化见下图

Parse Tree

[!EXAMPLE]

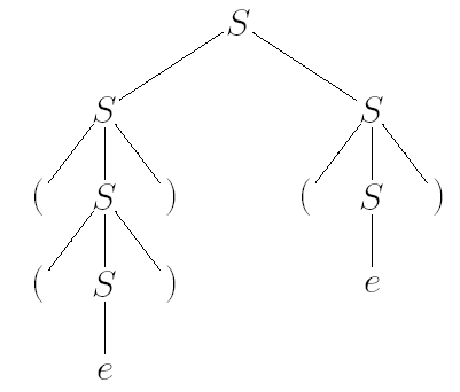
对于一个 CFG 文法为 \(S\rightarrow e,S\rightarrow SS,S\rightarrow e (S)\)，得到 \(SS\Rightarrow(())()\) 有两种办法

用树状图画出来，可以发现这两其实该做的都做了，就是做的顺序不一样

对于一个 parse tree

• node: \(V\) 里的元素
• root: \(\Sigma\) 里的元素
• leave；\(S\) 里的元素

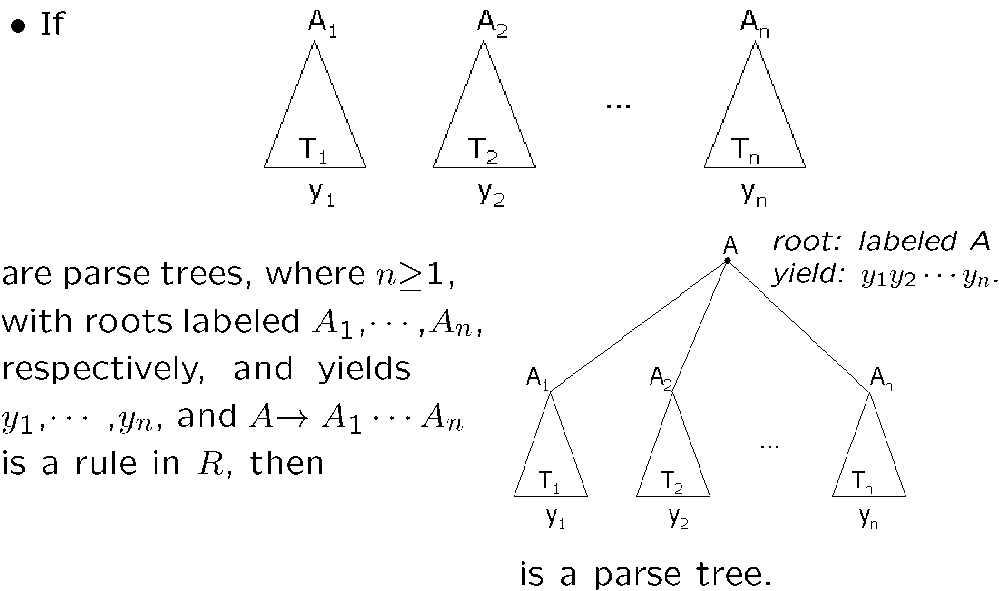
[!NOTE] parse tree formal defination

多个语法树共同连接于一个新 root，可以生成一个新的语法树

基于上面三种规则生成的都叫语法树

语法树是推导关系（derivation）的等价类

[!NOTE] 推导关系（derivation）的相似性

如何判断两个 derivation 是 similar 的

preceds

说白了就是两个 derivation 只有一步推导的结果不一样，而且是有迹可循的

leftmost 即，推导过程中永远只对最左边的字符串应用规则

我们有以下结论，即只要有起始符 \(A\) 能生成字符串 \(\omega\) 的这么一个推导过程，那么就一定有对应的语法树，且一定能找到对应的 leftmost 或 rightmost 的推导过程

[!EXAMPLE]

下面的例子中，我们发现 similar 的 derivation 不一定构成 preceds 关系

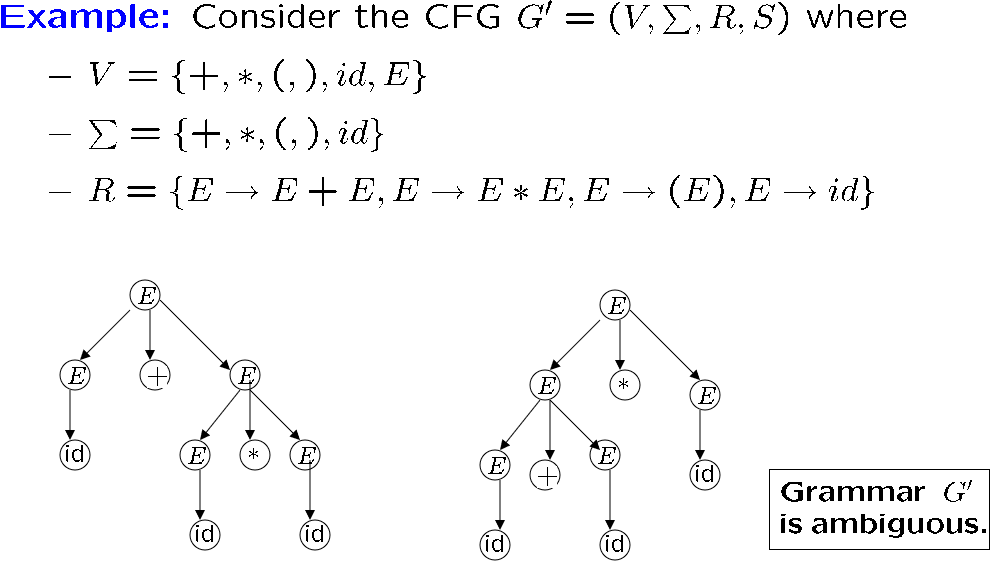
可见一个字符串的生成可以对应很多语法树，这会造成歧义 ambiguity

[!EXAMPLE] ambiguity

Pushdown Automata

比 FA 能力更强的机器模型来了

这个机器基于 FA，但 FA 只能读

为了实现读与写，PDA 进一步增加了一个 stack

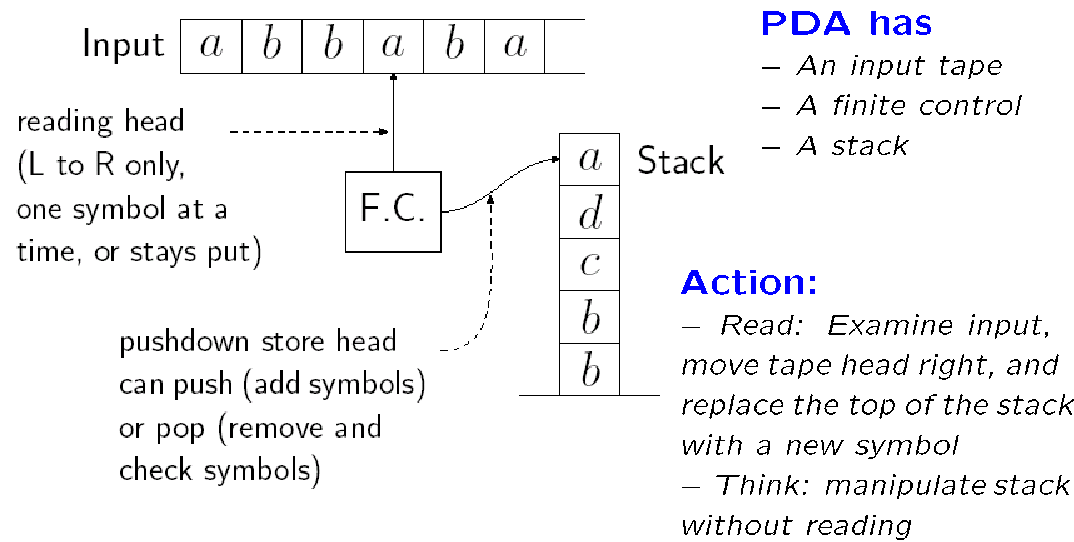
每次读的时候会用新的符号更新一次 stack

[!NOTE] PAD 的行为

PAD 可以进行读，读不仅会造成状态转移，而且会修改 stack top

读完后会移动 tape head

如果读取了空字符 e，就不移动 tape head

确切说不是“读取了空字符”，而是空字符情况下我们就可以进行状态转移，可以修改 stack top，即我们读取 tape 前可以停留在此处额外做操作

由此可见 PDA 是非确定性的

REMARK

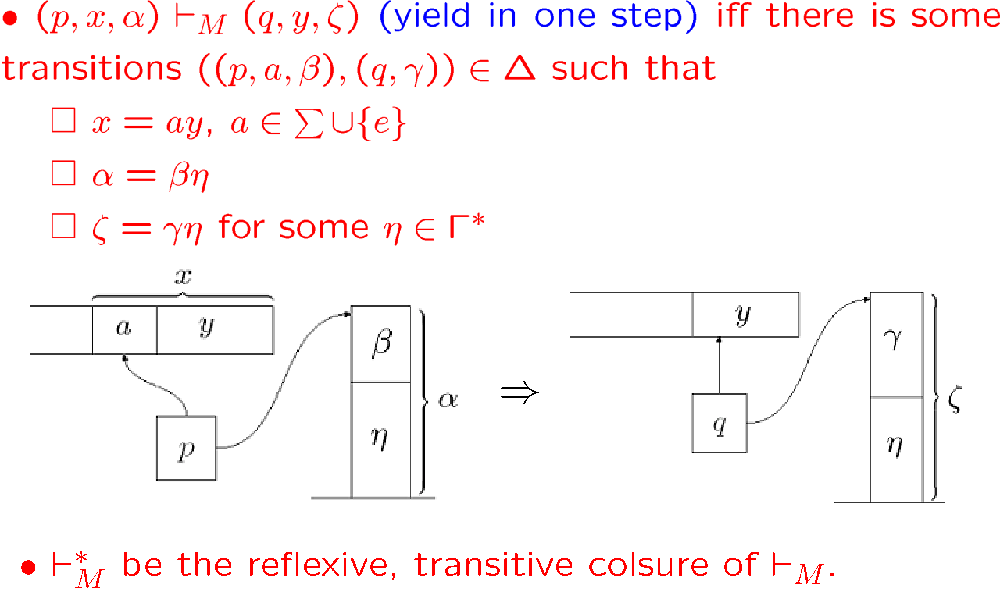
一步计算与多步计算：

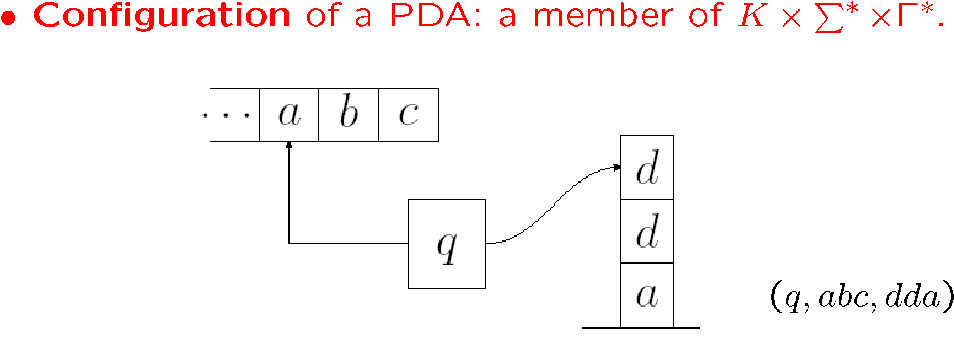
configuration 就是指某一时刻的 PDA

[!NOTE] PDA acceptance condition

1. 输入的字符串消耗掉
2. stack 清空
3. 到达结束状态

[!EXAMPLE]

[!EXAMPLE]

是不是很简单，有一个 stack 方便很多