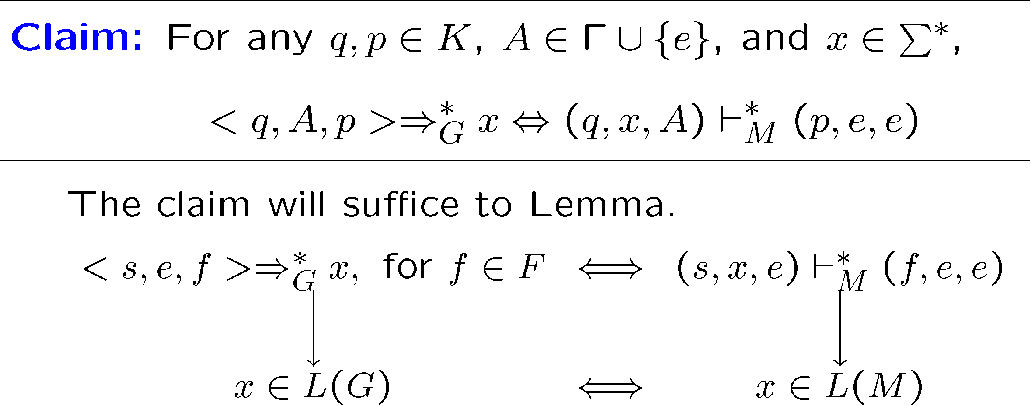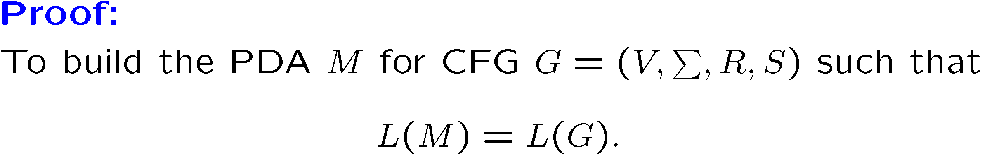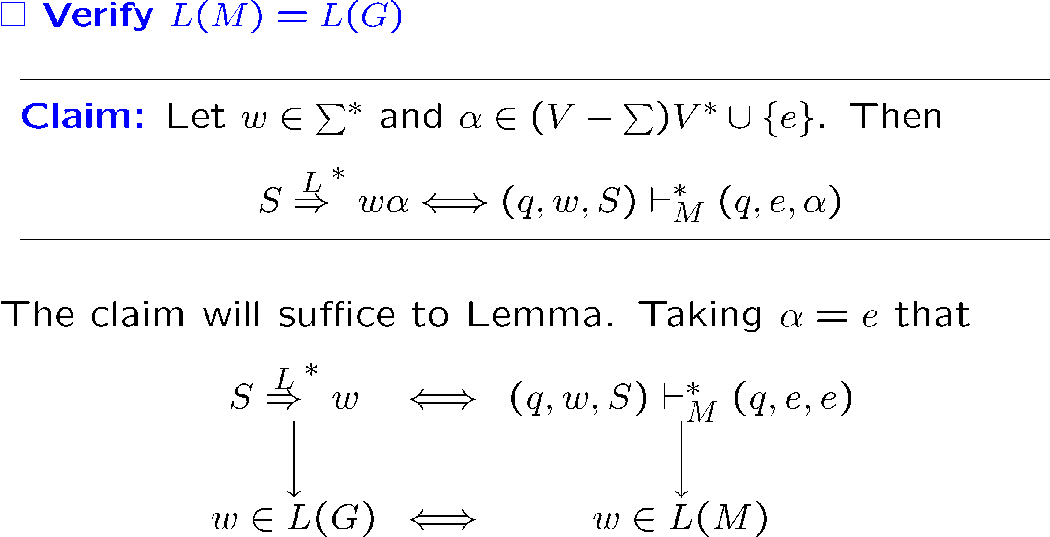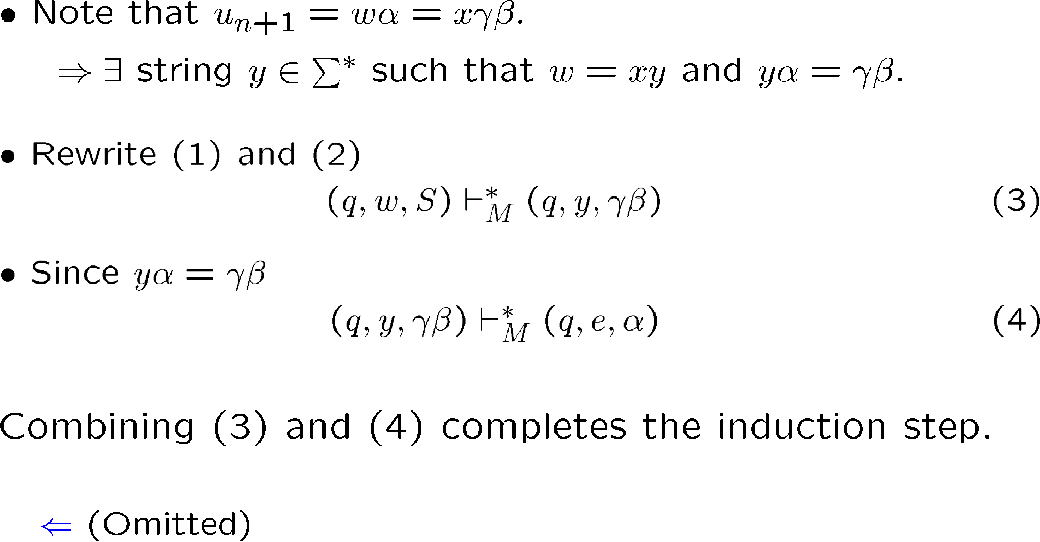Skip to content

3.1 PDA 与 CFL

:material-circle-edit-outline: 约 485 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

PPT 智云课堂 计算理论（本）2024-11-18 第 1-2 节

PDA 与 CFL

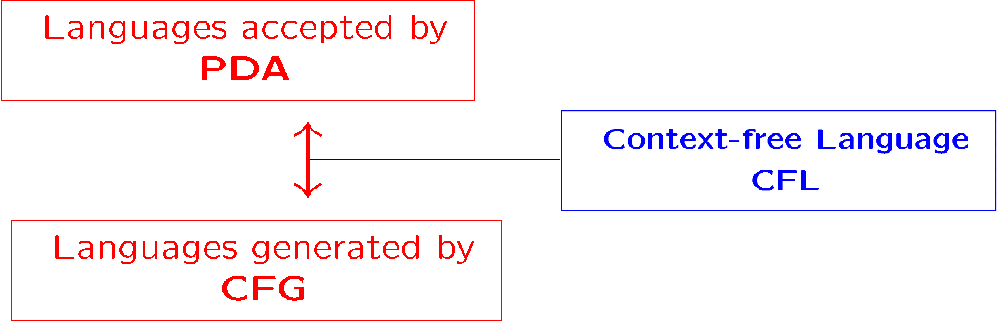
image-20241125123625778

PDA 能接受的语言类就是 CFL

image-20241125123553042

我们将从两个方向证明此事：根据 CFG 构造对应的 PDA

根据 CFG 构造 PDA

[!NOTE] Lemma：任何 CFL 都能有 PDA 将其接收（只要是 CFG 生成的语言一定能有 PDA 进行接收）

image-20241125123843276

[!NOTE] 根据 CFG 构造 PDA

对于 CFG 生成的 CFL，我们就设计一个可以接收其 leftmost derivation 的 PDA

image-20241125124054695

设计如下，注意这里 PDA 的 \(\Sigma\) 就是 CFG 的终结符集合

image-20241125124125875

只需要两个状态，三个转移关系：

  1. 把起始符压入栈
  2. 把 stack top 进行规则替换
  3. stack top 是终结符时可以 pop
    • 因为只有非终结符可以进行替换

[!EXAMPLE]

这里的 CFL 是带中心标志的回文

image-20241125125048374

image-20241125125055964

[!NOTE] 证明（没看）

我们将证明，这个设计出来的 PDA 能接受的 CFL 就是这个 CFG 能生成的

我们给出以下断言，其可以证明我们想证明的东西

image-20241125125847391

image-20241125125855423

image-20241125125905002

image-20241125130034613

根据 PDA 构造 CFG

我们尝试根据 PDA 设计相应的上下文无关文法

[!NOTE] Lemma：能被 PDA 接受的语言都是 CFL

image-20241125130724526

Define

[!NOTE] simple PDA

image-20241125130859278

注意 \(\Gamma\) 是字母集合，所以这里是指 \(\beta\) 只能有一个字符，即 stack 读只能读一个字符

写 stack 的时候（即替换）最多只能写两个字符

Convert

就是把 “读很长的字符串” 这个动作分解为很多个 “读一个个字符” 动作

先看前后的 PDA 怎么定义的

image-20241125131432147

我们看看怎么分解，先将读进行分解

image-20241125154345377

再将写进行分解

image-20241125154416207

特别的，输入 \(e\) 时，我们依旧要保证输入的是一个字符，所以我们从 stack 借一个字符，拿出来后再写进去

image-20241125154443226

Building

没弄懂

最后我们根据上面得到的 simple PDA，构造一个对应的 CFG

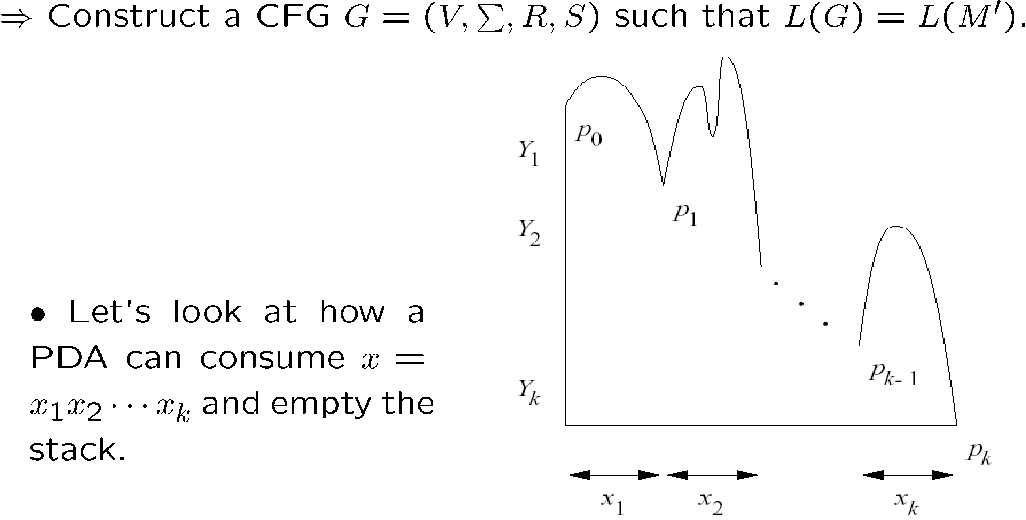
image-20241125154535472

image-20241125155918826

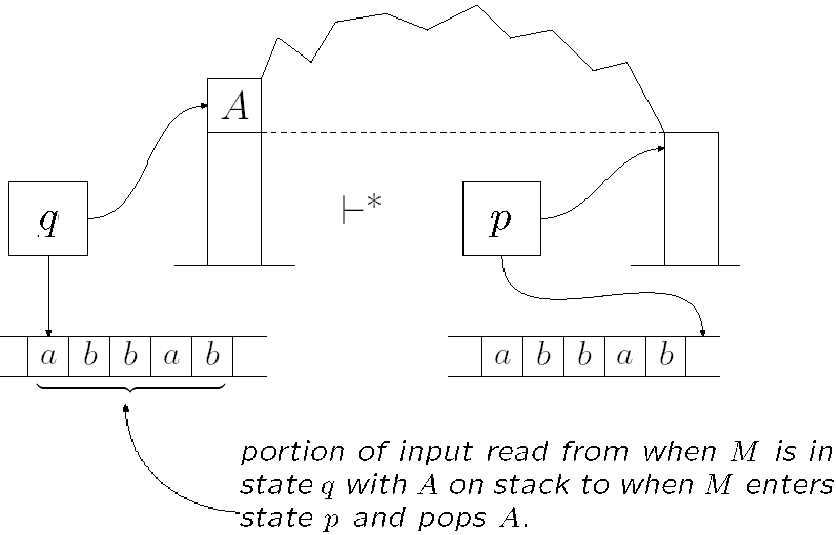
image-20241125155926963

image-20241125160026112

第一处的小 s 少了个撇

image-20241125160141591