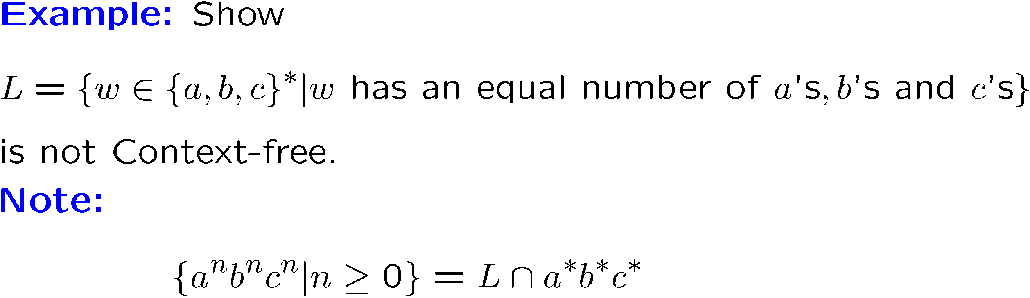Skip to content

3.2 非 CFL 语言

:material-circle-edit-outline: 约 255 个字 :material-clock-time-two-outline: 预计阅读时间 1 分钟

非 CFL 语言

CFL 的闭包（封闭性）

首先确定 CFL 的边界，我们可以确定 CFL 的闭包

image-20241125160723693

image-20241125160728612

特别的，我们可以确定，CFL 与正则语言的交集是 CFL

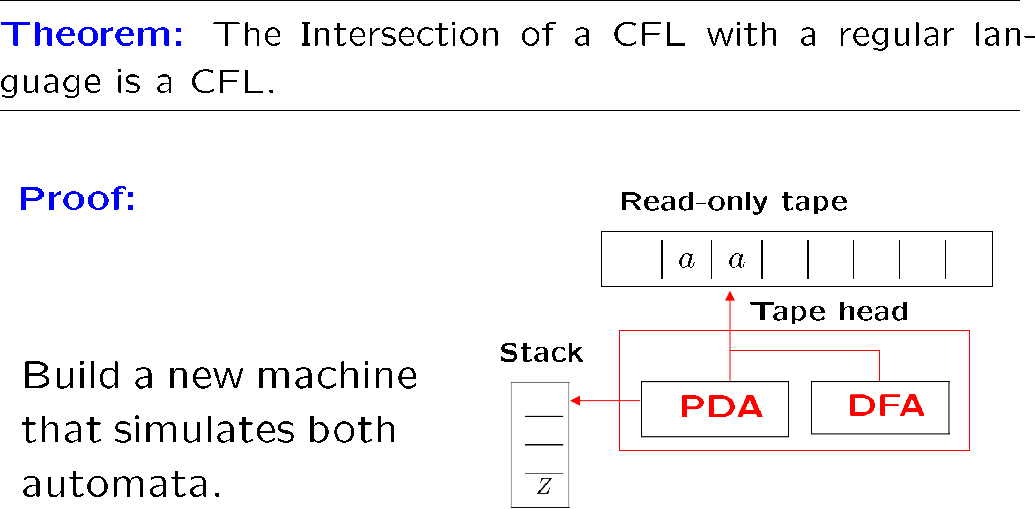
image-20241125160902615

直接把两个机器并行就行了

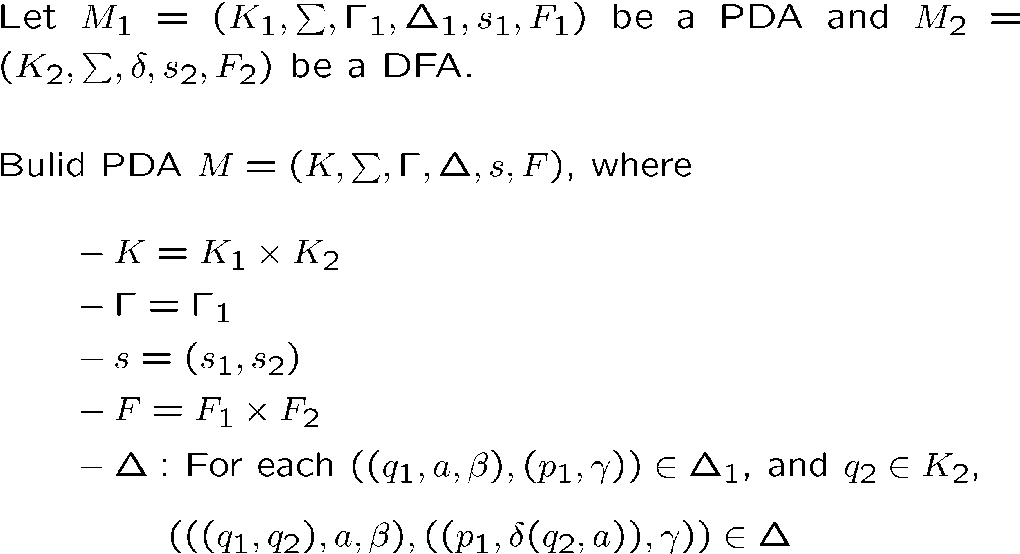
image-20241125161038229

交和补是不封闭的

image-20241130101350391

[!PROOF]

image-20241130101402695

[!EXAMPLE]

image-20241125160919800

Pumping Theorem

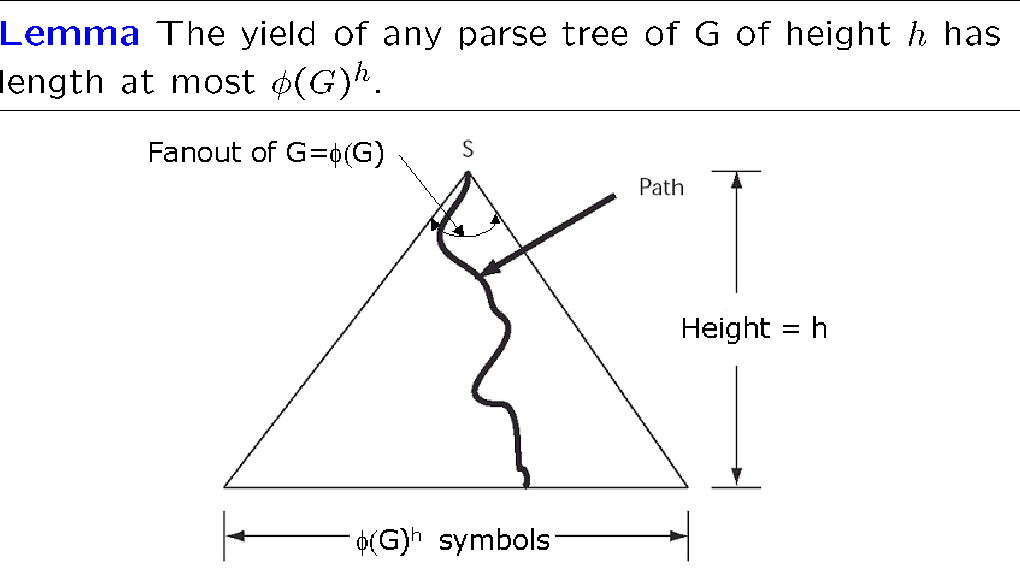
[!NOTE] Lemma

image-20241125161542401

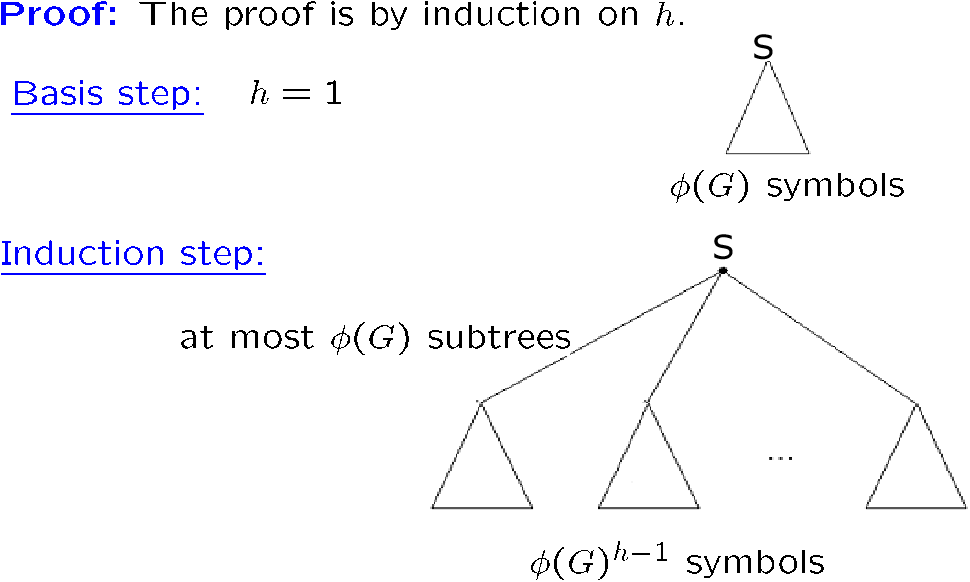
废话，就是对于一个树，每个结点有 \(\phi\) 个子节点，那么最多有 \(\phi ^h\) 个叶子

image-20241125161620409

image-20241125161627879

[!NOTE] Proof

image-20241125161642147

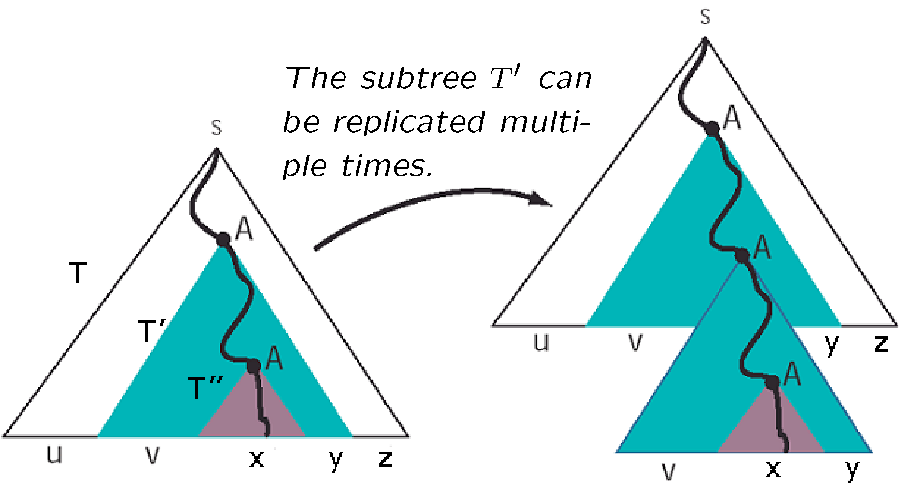
我们这选取了一个特定长度的字符串 \(\omega\)

image-20241125161646309

如此能确定 T 存在一条路径长度会大于非终结符数量，所以确定这条路径上有两个结点对应同一个非终结符

然后根据语法树生成规则，我们就可以无限生成了：

image-20241125161655651

与正则语言的泵定理类似，这个泵定理常用于证明某个语言不是 CFL

image-20241130100857687

[!EXAMPLE] 证明某个语言不是 CFL

image-20241125161708812

image-20241130100257922

注意 \((abc)^n \ne a^nb^nc^n\)

[!EXAMPLE]

image-20241130100938145

素数不可能被表示为等差数列

[!EXAMPLE]

image-20241130101152361

CFL \(\cap\) regular 还是 CFL