Skip to content

3.3 string是否属于 CFG

:material-circle-edit-outline: 约 555 个字 :material-clock-time-two-outline: 预计阅读时间 2 分钟

判断某个字符串是否属于某个 CFG

计算理论（本）2024-11-18第1-2节 PPT

image-20241130101823342

CFG 和 PDA 的相互转化，以及判断字符串是否属于某个 CFG，都有多项式时间内的算法

[!NOTE]

  1. 不存在判断两个 CFG 是否等价的算法
  2. 我们从 CFG 生成的 PDA 是不确定性的

image-20241130102321221

有爆算的方法，当然还有动态规划的方法

image-20241130102353364

使用动态规划需要先将语法转化为 Chomsky 范式

Chomsky NF

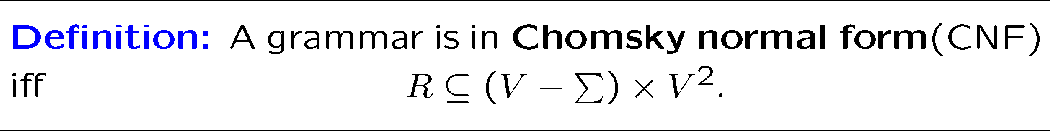
image-20241130102605960

即，CNF 的规则，都是从一个非终结符生成 长度为 2 的字符串

[!NOTE]

这类语法生成的字符串长度不会小于 2

image-20241130102800365

将 CFG 转化为 CNF

我们可以证明，任意 CFG 都可以生成 CNF 的 CDG

后者的 \(L(G)\) 只比前者少了空字符串和长度为 1 的字符串

image-20241130103035450

这个理论的证明就是转化步骤

我们针对原语法中不同的规则分别处理，分三步走

  1. 处理生成长度大于 2 字符串的规则
  2. 处理生成空串的规则
  3. 处理生成长度 1 字符串 或 推出另一个状态 的规则

image-20241130103452215

第一步，处理长规则

就是拆分成多个长度为 1 的短规则，留到第三步继续处理

image-20241130103417717

第二步，处理空规则

先把所有可能生成 \(e\) 的规则放入一个不知道什么符号的集合，算法就是先把这个集合设为空集，然后循环找能直接推导出集合内符号的规则，加入集合，如此循环

image-20241130103424504

然后对于整个规则集合 \(R\) 中的所有规则，检查某条规则 \(X\) 推导出的结果中是否存在某个规则 \(Y\) 属于上面那个集合里的

如果有，就将 \(X\) 复制为 2 个，一个有 \(Y\)，一个没 \(Y\)

如果有多个 \(Y\) 同理，见下图的例子

image-20241130103509652

如此，我们就能去掉所有空规则了

第三步，处理短规则

也是先把短规则全放入一个集合，算法自己看

image-20241130103531261

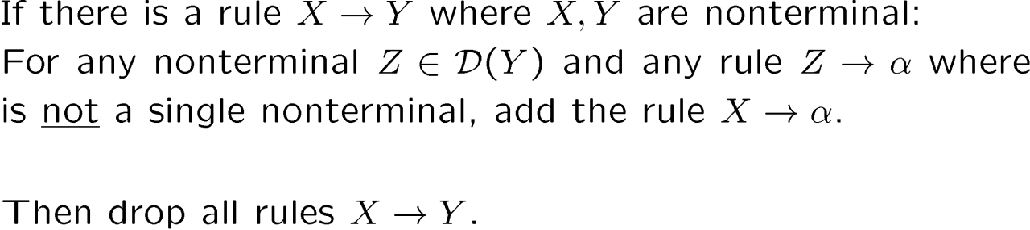
image-20241130105748943

image-20241130105758373

看例子吧，不懂

例子

image-20241130103553059

image-20241130103556700

判断某个字符串是否属于某个 CFG

采用动态规划的方法

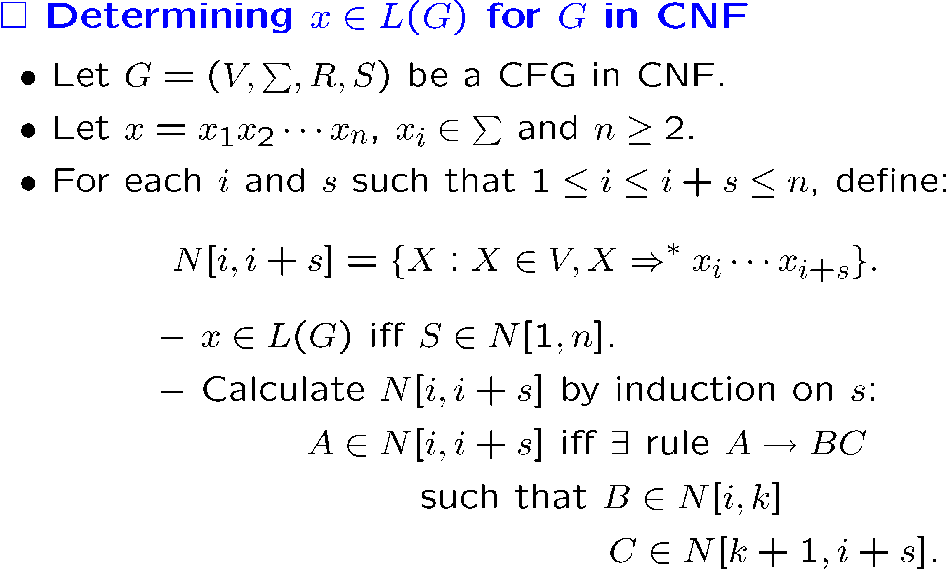
image-20241130110235765

image-20241130110239169

[!EXAMPLE]

image-20241130110317958